I’ll be honest with you: I remember first learning about Bloom’s Taxonomy when I was getting my teaching credential but I never really thought it was that big of a deal. I had a decent understanding of what it was and how you could implement it. What I didn’t get was why it mattered.
As we transition to the Common Core State Standards where Webb’s Depth of Knowledge (DOK) is the taxonomy of choice, the sentiment remained: why does depth of knowledge matter? I recently had an eye-opening experience that has helped me realize that depth of knowledge is more critical than I ever realized and I want to share that experience with you so you can understand what we should be working towards.
I was working with a strong and motivated team of seventh grade math teachers in my school district. We were in the process of creating an assessment to measure students’ understanding of CCSS 7.G.4 which states, “Know the formulas for the area and circumference of a circle and use them to solve problems; give an informal derivation of the relationship between the circumference and area of a circle.”
Area and circumference of circles was previously a 6th grade standard in California. On the outgoing California Standards Test (CST), this standard was assessed using questions like the ones below from the released test questions. All of the released test questions for this topic were DOK 1.
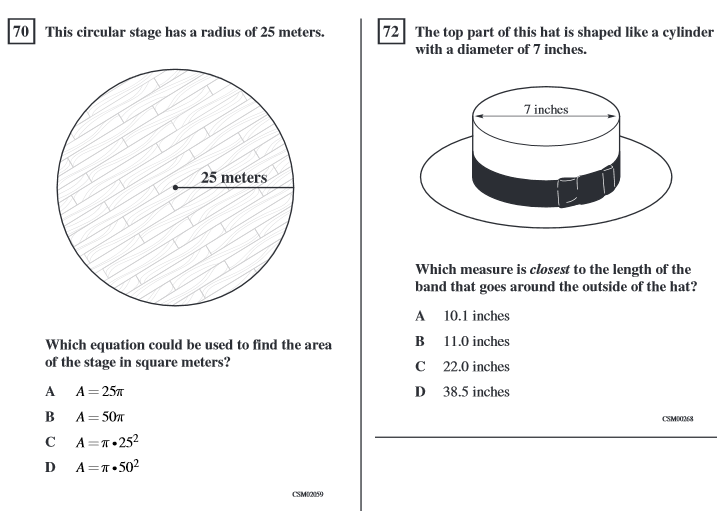
Accordingly, we decided to include two DOK 1 questions like these in the assessment.
Most students answered these two DOK 1 questions correctly. Here are ten students who exemplify the process many of their peers used.
- 68.26% correctly answered the circumference question
- 78.59% correctly answered the area question
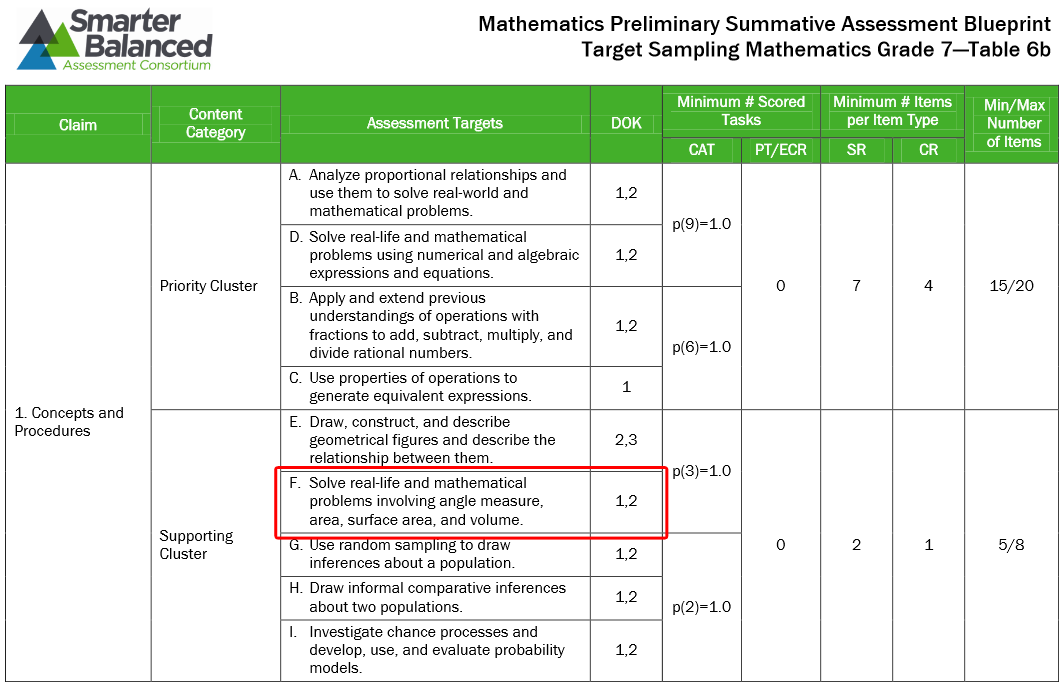
In years past, that would have been the extent of the assessment. However, we wanted to know the depth of knowledge that students would be expected to demonstrate under the Common Core State Standards. To determine this, and since California is a member of the Smarter Balanced Assessment Consortium (SBAC), we looked at the SBAC Preliminary Test Blueprint which lists the DOK levels that students will be assessed at. As you can see below, it shows that the cluster this standard is a part of will be assessed at DOK 1 and/or 2.
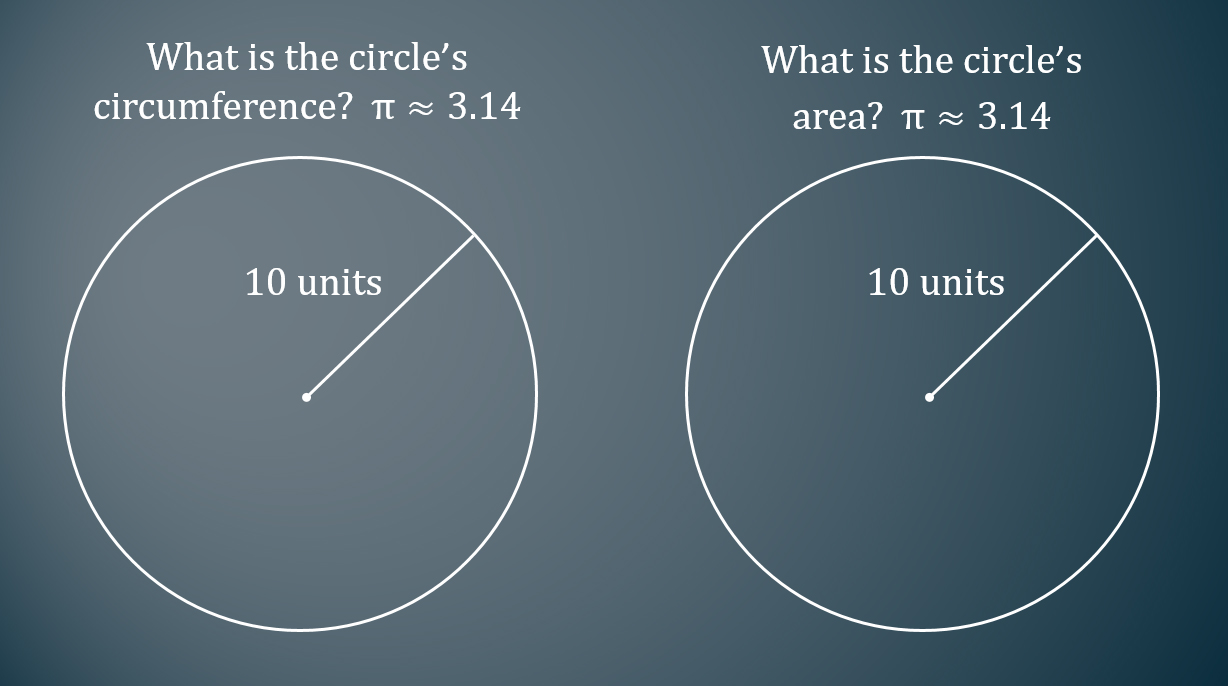
However, after seeing the SBAC Preliminary Test Blueprint we wondered, “What does a DOK 2 question for this standard look like and where would we find one?” We couldn’t find one online or in our textbook so we spent about 15 minutes thinking of ideas, and eventually came up with this question below:

It honestly didn’t seem that impressive or that big of a difference to us. We weren’t even sure if it really reached the DOK 2 level. Ultimately we decided to include it on the assessment. We graded this question by hand using the two-point SBAC rubric for evaluating constructed response questions which states:
- For full credit (2 points):
- Student reaches the correct conclusion AND student provides sufficient reasoning to support this conclusion.
- For partial credit (1 point):
- Student reaches the correct conclusion but does not provide sufficient reasoning to support this conclusion OR
- Student does not reach the correct conclusion but provides reasoning to support this conclusion that contains a minor conceptual or computation error.
Here are the same ten students answering the DOK 2 question:
Of the ten students, only one earned two points. Six earned one point and the remaining three earned zero points. As a comparison, of the 396 seventh grade students assessed only 12.12% earned two points on the DOK 2 question.
We were shocked. We thought that there might be a difference in results between the two types of questions but we didn’t think it would be this dramatic.
Some interesting additional facts:
-
97.92% of the students who correctly answered the DOK 2 question also correctly answered both of the two DOK 1 questions. So, correctly answering the DOK 2 question was a strong predictor of students’ ability to answer both of the DOK 1 questions correctly.
-
10.61% of the students who correctly answered both of the two DOK 1 questions also correctly answered the DOK 2 question. So, correctly answering both of the DOK 1 questions did not mean students would be able to answer the DOK 2 question.
- 28.28% of the students earned only one point. All of them earned one point by choosing Circle B and providing insufficient reasoning. Among the most common explanations determined to have insufficient reasoning were:
- “Area is always bigger than circumference”
- “Area is everything inside the circle and circumference is everything outside the circle. There is always more space outside of a circle.”
- 59.59% of the students earned no points meaning they picked circle A and had insufficient reasoning.
Here were our takeaways:
- We have had a false belief that students were proficient with this standard because we assessed them with questions that measured shallow depths of knowledge.
- We don’t know exactly why students got the DOK 2 problem wrong and it requires more investigation. Did they get the DOK 2 problem wrong because:
- the DOK 1 problems asked students to plug in the radius and go forward while the DOK 2 problem asked them to work backwards to find the radius?
- the DOK 1 problems told students exactly what action to take (i.e., find the area or circumference) while the DOK 2 problem did not give specific instructions and students had to figure out how to connect the two circles?
- It isn’t fair to assess students at higher DOK levels when we haven’t incorporated them into our instruction. Hence, we better incorporate them into our instruction.
- Finding DOK 2 and DOK 3 questions can be really challenging. Hence, my real life colleague, Nanette Johnson, and I created a website called Open Middle (based on inspiration from a Dan Meyer presentation) where we have a growing number of higher DOK problems. Check it out and you will find a variety of problems you can immediately use.
What other takeaways do you have that we missed?


I have a strong affinity for Webb’s DOK but for different reasons, perhaps. I find the language use that Webb emphasizes to be really important when I think about the questions that I ask. I am, unfortunately, not as surprised to see the difficulty in the DOK 2 question here. I am reminded of an experience I had teaching Geometry. At the end of a unit on circles I had asked the students on numerous occasions to identify centers and points on the circle when given an equation. On a unit test, I asked them to write their own equation, to identify the center, four points on the circle and any x and y intercepts. Most students were able to do this correctly but they complained loudly about this. When I returned the tests and we discussed the question I asked them why they were upset. I jokingly told them I was doing them a favor by giving them freedom of choice. They responded, almost in unison, ‘We don’t want freedom of choice, just tell us what to do’
This, I think, is a pretty common reaction among math students. Unfortunately, many of them have been trained to simply try to know what formula to use and concentrate on how to use it.
Thanks Jim. Based on your experiences, it looks like there will be some student push back when getting them to think more deeply. I believe it is a worthwhile, albeit occasionally painful, endeavor. Hopefully they will become more accustomed to it over time.
A problem that looks at circle circumference:
http://fivetriangles.blogspot.com/2014/01/129-circles-in-circle.html
Wow. There are a lot of great problems on your site. I will have to give it a deeper look the next time I am looking for problems. Have you thought about tagging the problems with a CCSS standard? Thank you for sharing it.
I am trying to access your site, as well, and can’t see it because I need to be invited. Five Triangles, would you be willing to invite me? How do I connect with you?
Can you please grant me access to view your page. Would really like to see your five triangles problem.
Thanks
I’m just seeing this post and am wondering if you would grant me access to your blog? Thank you for considering. -Angie
Robert, thanks for posting this thought-provoking material. As I watched the students struggle with your DOK 2 problem, I thought, “How would I cue students in a whole-group discussion to get them to solve this?” Here are some ideas:
*Present the problem and give students some number of minutes to try it. Let students discuss their work in pairs or small groups.
*Pull the class back together and invite students to share ***strategies*** for solving the problem — i.e. not detailed solutions, but general strategies. Here are some I came up with, and which I would also expect students to be able to generate:
*S1: You know the area of one circle. If you could somehow find the area of the other circle, then you can compare the two to decide which one is “bigger.”
*S2 — the cousin of S1 — you know the circumference of one circle. Find the other circumference and pick the one that’s bigger.
*S3: find the radius of each circle. The one with the bigger radius wins!
It strikes me that in all three cases, there is a common theme: they represent efforts to *understand the problem.* i.e. they answer the question, “What does it mean to say that one circle is bigger than another?” S1: bigger area means bigger circle. S2: bigger circumference means bigger circle. S3: bigger radius means bigger circle.
And so now we have a cue in case the room is quiet when you ask how to solve the problem: “You guys seem stuck. Do me a favor and forget all about these two circles with the 36’s and stuff. Let’s hit the reset button: I’ve got two circles and I want to know which one is bigger. How can I find out? Discuss this with a partner and be ready to report back in 30 seconds.”
Last thought, reflecting on that last move: there is something deep happening when I say “forget the 36’s.” I’ve whittled the problem down to its core: I’m supposed to compare the size of two circles, and I need to find a way to make that happen. Only when I’ve figured out how to do that does it matter what specific information I have about those two circles — A = 36 or C = 36. At that point, it really is a matter of algebra or whatever you want to call it — but I’m not shocked if students can’t close that gap as well!
All great stuff — thanks for the chance to reflect on good math and good teaching.
James, what a great comment. There are lots of spot on points you make. This is exactly the goal I was hoping for with this post. I almost never gave students DOK 2 and DOK 3 problems so I had a false sense of students’ understanding. Once we realize that these gaps exist, then the challenge begins of addressing them. Your strategies seem like a great start and we had come to similar conclusions when we discussed it as well. Thank you for adding to the conversation.
I feel there is more of a grey area between DOK level 2 and DOK level 3 problems than DOK level 1 versus DOK level 2 problems, for instance. The DOK level 2 question you created, at first glance, appeared to me to be a DOK level 3 question. Could it be justified that question could be classified as a DOK level 3 question? I viewed the first part (which circle is bigger?) as DOK level 2 and the second part (how do you know?) as DOK level 3.
Hi Sonny. In general, I am less concerned with defining the precise moment a problem moves from one DOK level to the other and more concerned with simply incorporating more problems that are not DOK 1.
Specifically addressing your question, I don’t feel that articulating your reasoning affects the DOK level much. Have you seen this post? http://robertkaplinsky.com/tool-to-distinguish-between-depth-of-knowledge-levels/ None of these problems mention explanations. So, it’s more about the strategic thinking.
What do you think?
I think your point about incorporating more DOK 2 and 3 problems in class is important, but I also think that sometimes teachers give the same problem ahead of time with different numbers, say a circle with an area of 25 vs a circumference of 25. It kind of defeats the purpose of having authentic thinking on an assessment by turning this type into a recall problem (can you remember how we solved this in class?). I do think there is a way to practice DOK 2+ in class without replicating problems, but I think it’s an important thing to keep in mind.
Yeah Bonnie. I’m on the same page as you.