How Big of a Problem are Littered Cigarette Butts?

Download

The Situation

The Challenge(s)

How big of a building would all the cigarette butts littered every day in the United States fill? A classroom? An auditorium? A stadium?
How long would it take to fill a ____________?
How long would a line of cigarette butts littered each day measure?

Question(s) To Ask

These questions may be useful in helping students down the problem solving path:

Consider This

It has been said that “There are three kinds of lies: lies, damned lies, and statistics.” As such, it is worth discussing the general accuracy of statistics with students.
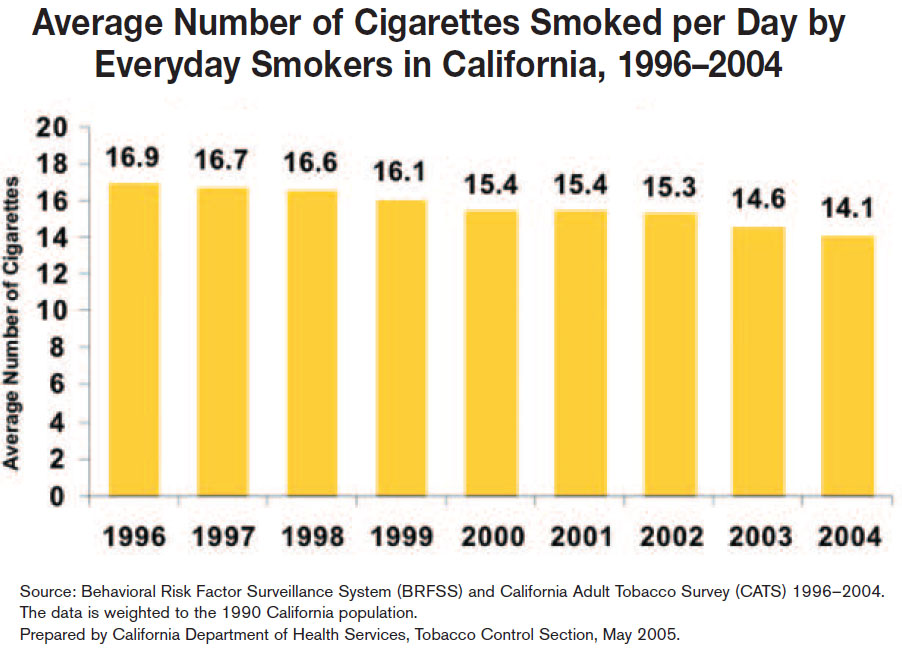
Students may begin by finding the number of smokers (43.5 million as of 2010) and on average how many cigarettes they smoke each day (14.1 as of 2004).
Using that information and that only 90% of cigarette butts are littered (10% are properly disposed), you get 552,015,000 cigarette butts littered each day.
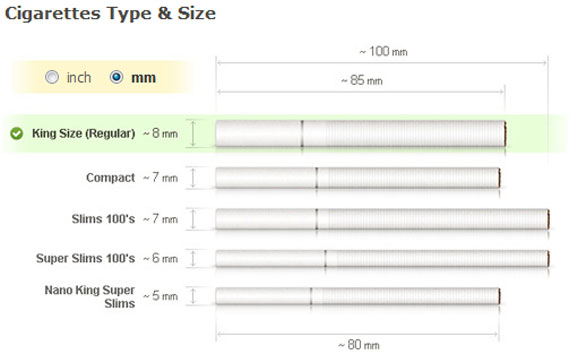
With that number of littered cigarette butts you can multiply it by an estimate for the volume of a cigarette butt (1.758 cubic centimeters based on King Size and a cylinder with a ~8 mm diameter and ~35 mm height) using its dimensions.
This gives a volume of ~970 cubic meters. Students can then determine the volume of a classroom and cafeteria. The volumes of an auditorium and stadium are given.

What You'll Need

Content Standard(s)

CCSS 5.MD.3 – Recognize volume as an attribute of solid figures and understand concepts of volume measurement.
CCSS 5.MD.4 – Measure volumes by counting unit cubes, using cubic cm, cubic in, cubic ft, and improvised units.
CCSS 5.MD.5 – Relate volume to the operations of multiplication and addition and solve real world and mathematical problems involving volume.
CCSS G-GMD.3 – Use volume formulas for cylinders, pyramids, cones, and spheres to solve problems.
CCSS G-MG.1 – Use geometric shapes, their measures, and their properties to describe objects (e.g., modeling a tree trunk or a human torso as a cylinder).

Source(s)

Download