How Far Apart Are Exits On A Ring Road?

 
The A10 motorway is a highway in the Netherlands.  This highway is called a “ring road” because it forms a relatively circular pattern around the city of Amsterdam.
 

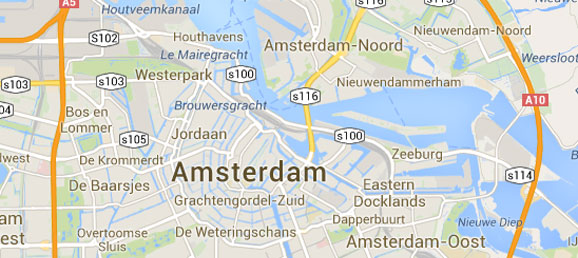
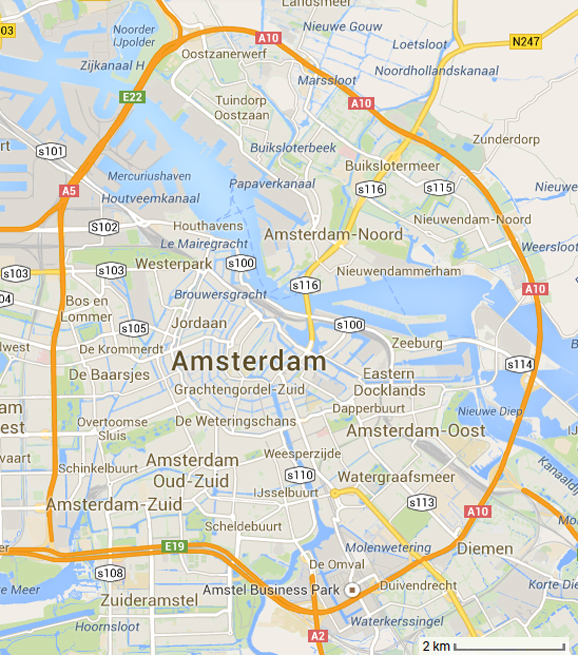
• How many kilometers do you have to drive on the A10 motorway to drive from the exit for s116 to the exit for s113?

 

These questions may be useful in helping students down the problem solving path:

• What options do we have for measuring the distance between the exits?
• How would we measure the distance between the exits if there was a straight freeway that connected them?
• How can we use that technique to help us make a better approximation?
• What shape does that portion of the highway resemble?
• What information do we know about circles that we can use to help us determine the distance?

 

This lesson is useful as a context for finding arc lengths or for developing conceptual understanding of circumference as measuring a circle’s perimeter using infinitely many infinitely small line segments.  I have provided two maps (courtesy of Google Maps) to help students in this process.  One is missing the scale and the other includes it.  It may be interesting to begin by using the one without the scale and hoping that students realize this to be a critical piece of information.

Two potential approaches for solving this problem come to mind:

• Measuring the distance by using more and more line segments to get a better approximation.
• Approximating that portion of the ring road as part of a circle, determining the circle’s center, and finding the length of that portion of the arc.

I believe that there is value to both approaches and the conversation that comes out of comparing their merits.

With the first approach, students may measure directly from one exit to the other and assume that the real answer is a little more than what he or she got.  Another student may measure from s116 to s114 and add that to the distance from s114 to s113.  That should prove to be more accurate.  Repeating this process using more and more line segments should help students realize that the more line segments used, the more accurate the measurement.

With the second approach, students have to think of the map as illustrating a portion of a circle.  The image below shows how using a protractor, the arc between the exits measures roughly 118.5º.  The circle’s radius is also approximately 4.49 km.

 

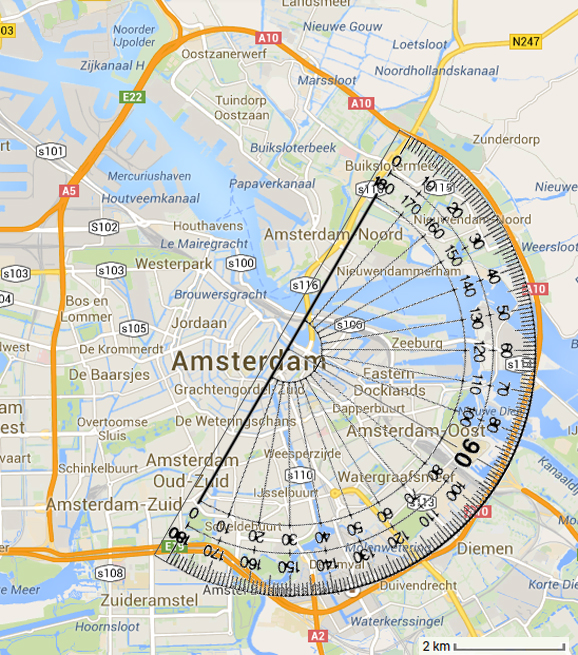
With this information and knowing that a circle’s circumference is 2Πr, we get that the circle’s circumference is approximately 28.21 km.  The portion of the circle that we are focusing on is approximately 118.5/360 of a circle or about 32.92% of the entire circumference.  Multiplying 32.92% by 28.21 km gives us a distance between the exits of about 9.29 km.

According to the Wikipedia entry for the A10 motorway (below), exit s116 is at kilometer 4 and exit s113 is at kilometer 13 giving us a distance of about 9 km which validates our calculations.

 

• Map without scale

• Map with scale

 

• CCSS G-C.5 – Derive using similarity the fact that the length of the arc intercepted by an angle is proportional to the radius, and define the radian measure of the angle as the constant of proportionality; derive the formula for the area of a sector.

 

• Wikipedia – A10 Motorway
• Wikipedia – Ring Road
• Google Maps