How Much Bigger Should They Make Zoolander’s School?

 

• How many times bigger should the school be?

 

These questions may be useful in helping students down the problem solving path:

• How big would the school be if it was twice as big?
• How big would the school be if it was five times as big?
• What size would a student have to be to go to the school if it was ____ times bigger?
• How can we determine how many times bigger the school should be?
• Since we don’t have the exact information we want, what other methods could we use to determine how much bigger the school should be?
• How can we determine if his answer is correct?
• What would be a wrong answer?
• How large can we make the answer and still ensure that it is correct?

 

If you’re not familiar with the movie Zoolander, it is about a male model named Derek Zoolander (played by Ben Stiller) who means well but is not the sharpest tool in the shed.  In this scene he learns about a school that will be built in his name.  He doesn’t realize that he is being shown a model of the school and not the actual school itself and angrily tosses it to the ground.  He then states, after much thinking, that it needs to be three times bigger.  While his answer is technically not wrong (he said “at least”), it is a relatively inaccurate guess.

After briefly discussing the movie’s context, show students the opening clip from “The Situation.”  The part where Derek says “three” has been bleeped out so this should help students focus on “The Challenge” question.  Students will need to determine how many times bigger the school model should be.  I have thought of three methods for how students may approach this problem.  Obviously the estimates students make for the lengths may be different but the approaches should be similar:

Approach #1: Finding scale by comparing school model to actual school

Using the screen shot below where Zoolander is standing next to the school, they may use Stiller’s height to get an estimate for the height of the model and then compare it to an estimate for how tall the school might be in real life.

 

Using the information that Stiller is 5’7″ (below from IMDB), it seems like the school model is about 1.5 to 2 feet tall.

 

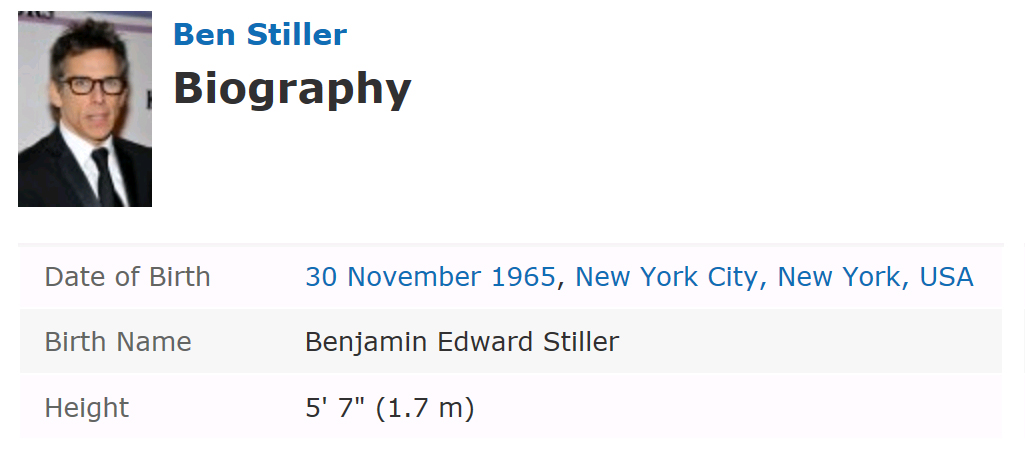
Next the student has to estimate how tall the real school would be.  Estimates will clearly vary but based on the picture below it seems like it would be about 13 stories tall if you include the large book sculpture on top.  I also assume that a story is 10 feet tall.

 

Using that information, then you have a model where 1.5 feet represents 130 feet (13 stories x 10 feet) so the school should be about 87 times bigger.

 

Approach #2: Finding scale by comparing Zoolander to height of people in the school model

Using the screen shot below where Zoolander is closely examining the school model, you can see little white figurines that represent people walking in front of the school.  They appear to be roughly one inch tall.  If you assume that the average person’s height is 6 feet tall, then you have a model that is roughly 1/72 (6 feet x 12 inches per foot) of its actual size.  So, the school should be roughly 72 times bigger.

 

Approach #3: Finding scale by comparing school model stories to average story height.

Using the screen shot where Zoolander is closely examining the school model, you can see that there are five stories in the building.  Each story appears to be a little more than 1″ tall.  Assuming that a story in real life is 10 feet tall and assuming 1 inch for the height of the story on the school model, then you have a model that is roughly 1/120 (10 feet x 12 inches per foot) of its actual size.  So, the school should be roughly 120 times bigger.

 

I recommend against focusing the student discussion on what the correct answer should be and instead on the commonalities and differences between their approaches.  Once students have their answers, play the “answer” video below:

 

Students’ reactions to the video may range from laughing at his humorous response to immediately questioning the validity of their own answer.  After giving students time to think about what Zoolander said, help students move from thinking he is wrong to determining what a less conservative estimate would be.  This conversation may include a discussion around the assumptions various students made and which assumptions are safer.

 

Check out how Amanda Beaulieu implemented this lesson with her students. She found that students used Zoolander’s nose as a unit of measurement and she has even translated it into French!

 

• CCSS 5.NF.5a – Comparing the size of a product to the size of one factor on the basis of the size of the other factor, without performing the indicated multiplication.
• CCSS 7.RP.2 – Recognize and represent proportional relationships between quantities.
• CCSS 7.G.1 – Solve problems involving scale drawings of geometric figures, including computing actual lengths and areas from a scale drawing and reproducing a scale drawing at a different scale.

 

• Zoolander on Wikipedia
• Ben Stiller on IMDB