What Michaels Coupon Should You Use?

 
You are buying arts and crafts supplies from Michaels this Sunday and have the two coupons pictured below to choose from.

 

• Which coupon will save you the most money?
• How much would the higher-priced item in Scenario 2 have to be to make both coupons save the same amount of money?

 

These questions may be useful in helping students down the problem solving path:

• Does what we buy matter when deciding which coupon to use?
• How can you prove someone is right or wrong?
• Why was the 40% off coupon only better to use in one scenario?

 

I recommend beginning the lesson by presenting the students with the two coupons but none of the actual products and asking them the challenge question of “Which coupon will save you the most money?”  I would imagine that students’ answers would include:

• 30% off entire regular price purchase
• 40% off any one regular price item
• How can I pick without knowing what I am buying and how much it will cost?

If you set it up as a class conversation where each student states which coupon he or she would use, I could see the three answers getting debated back and forth.  Hopefully students are eventually convinced that they need more information before they can decide on which coupon to use.

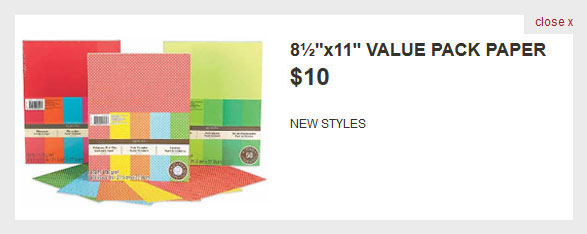
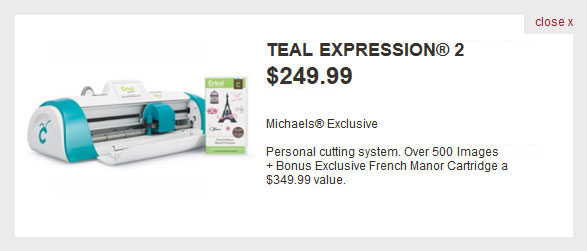
It was surprisingly challenging to find the prices of Michaels products and I ultimately decided to focus on one low and one high price item:

Low priced item:

 

High priced item:

 

I suggest presenting four scenarios, one at a time, to students where they predict which coupon will save them the most money, and then allow them to determine if they correct.  The four scenarios are:

Scenario 1

You are purchasing 3 of the low priced items.

• The 30% coupon would save you 30% of the $30 ($10 + $10 + $10) total for a total savings of $9.
• The 40% coupon would save you 40% of the highest priced item ($10) for a total savings of $4.

Therefore the 30% off coupon saves you $5 more.

 

Scenario 2

You are purchasing 2 of the low priced items and 1 of the high priced items.

• The 30% coupon would save you 30% of the $269.99 ($249.99 + $10 + $10) total for a total savings of $81 (rounded up from $80.997).
• The 40% coupon would save you 40% of the highest priced item ($249.99) for a total savings of $100 (rounded up from $99.996).

Therefore the 40% off coupon saves you about $19 more.

 

Scenario 3

You are purchasing 1 of the low priced items and 2 of the high priced items.

• The 30% coupon would save you 30% of the $509.98 ($249.99 + $249.99 + $10) total for a total savings of $152.99 (rounded down from $152.994).
• The 40% coupon would save you 40% of the highest priced item ($249.99) for a total savings of $100 (rounded up from $99.996).

Therefore the 30% off coupon saves you about $52.99 more.

 

Scenario 4

You are purchasing three of the high priced items.

• The 30% coupon would save you 30% of the $749.97 ($249.99 + $249.99 + $249.99) total for a total savings of $224.99 (rounded down from $224.991).
• The 40% coupon would save you 40% of the highest priced item ($249.99) for a total savings of $100 (rounded up from $99.996).

Therefore the 30% off coupon saves you about $124.99 more.

 

I hope students are curious about why the 30% off coupon was the best every time except for Scenario 2.  Hopefully a discussion will ensue and students will realize that for the 40% off coupon to save the most money, the extra 10% it saves (40% – 30%) must be more money than the money saved on the two other items covered by 30% off coupon.  Algebraically that looks like:

amount saved by 40% off coupon > amount saved by 30% off coupon

40% * highest priced item > 30% (highest price item + other item + other item)

.4 * x > .3 (x + y + z)

which eventually gives us:

.1 * x > .3 (y + z)

or in words, we save money with the 40% off coupon when:

10% off the highest priced item > 30% off the other two items

 

Once students have finished the four scenarios, you can ask the second challenge question: “How much would the higher-priced item in Scenario 2 have to be to make both coupons save the same amount of money?”  Many strategies will work to figure this out including guess and check.  However using the inequality above as an equation, we are asking, when the 10% off the highest priced item equals 30% off the other two items.  That gives us:

.1 * x = .3 (y + z)

Since we know that the other items in Scenario 2 are both $10 we can plug that in and get:

.1 * x = .3 (10 + 10)

.1 * x = 6

x = 60

 

We can verify that both coupons will save the same amount of money when the highest priced item is $60 using an altered Scenario 2:

Altered Scenario 2 (with higher priced item being $60)

You are purchasing 2 of the low priced items and 1 of the high priced items.

• The 30% coupon would save you 30% of the $80 ($60 + $10 + $10) total for a total savings of $24.
• The 40% coupon would save you 40% of the highest priced item ($60) for a total savings of $24.

Therefore the 30% off and 40% off coupons save you the same amount of money.

 

One last note… apparently there is a way to solve this problem in real-life with no math.  People will go up to the cashier and give her both coupons so she can scan them, one at a time, and tell you which will save you more money.  I haven’t decided if I am impressed or depressed by this.
 

I have done a lot of Photoshopping to the images used in this lesson.  This includes:

• Removing the expiration dates from the coupons
• Removing references to “Cricut” from the product originally called “CRICUT TEAL EXPRESSION 2” as I realized that Cricut brand products are excluded on the coupon.  I couldn’t find any other expensive products with prices so this was the easiest route.
• Enlarging the products pictures on both of the product info images.
• Changing the price of the paper from 3 for $10 to just $10.

 

Mr. Taylor has modified this task to make it relevant to students in the United Kingdom.  You may want to use his coupons instead.
 

• CCSS 7.RP.3 Use proportional relationships to solve multistep ratio and percent problems. Examples: simple interest, tax, markups and markdowns, gratuities and commissions, fees, percent increase and decrease, percent error.
• CCSS A-CED.3 Represent constraints by equations or inequalities, and by systems of equations and/or inequalities, and interpret solutions as viable or nonviable options in a modeling context. For example, represent inequalities describing nutritional and cost constraints on combinations of different foods.
• CCSS F-BF.1 Write a function that describes a relationship between two quantities.

 

• Michaels