How Tall Is Mini-Me?

 

 

• What fraction is Mini-Me of Dr. Evil?
• How tall would Mini-Me have to be to be one eighth of Dr. Evil’s size?
• How tall would Dr. Evil have to be if Mini-Me really was one eighth his size?

 

These questions may be useful in helping students down the problem solving path:

• What is a guess that is too low?
• What is a guess that is too high?
• What is your best guess?
• What is the closest unit fraction to your answer?
• Why is your answer different from what they said in the movie?

 

One important issue to think about from the very beginning is the lack of precision around the word “size”. This comes out because the video clip says, “He is exactly like you in every way… except one eighth your size.” Does that mean 1/8 your height? Does that mean 1/8 your volume? Depending on what you define it to mean, it will affect your conclusion.

To answer this question, students will need to know the heights of Dr. Evil (played by Mike Myers) and Mini-Me (played by Verne Troyer).  These images provide that information:

 

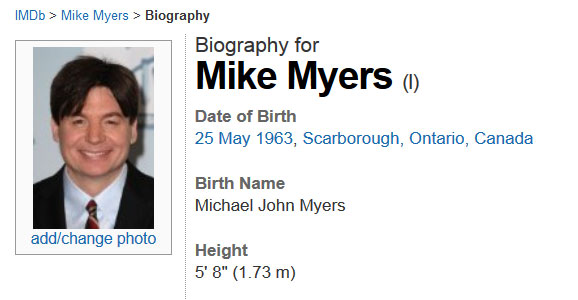
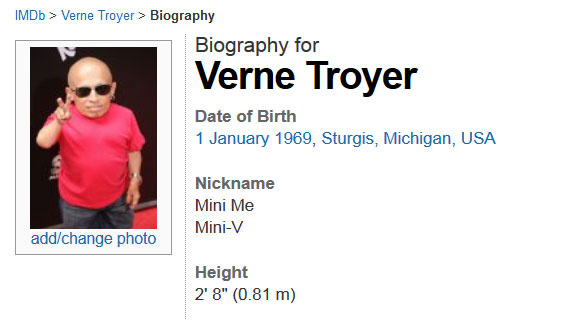
Something to note is that students may also get confused by the questions, “What is a guess that is too low?” and “What is a guess that is too high?”  For example, is one thousandth a guess that is too low or too high?

If you define size as height, then to figure out the answer to the challenge question, take Mini-Me’s height of 0.81 meters and divide it by Dr. Evil’s height of 1.73 meters giving us a decimal of approximately 0.47.  So, Mini-Me is approximately 47/100 the size of Dr. Evil.  At this point I would ask students, “What is the closest unit fraction to your answer?” as we want them to say one half.  It will be an interesting exercise for students to figure out if 47/100 is closer to one half, one third, one fourth, etc.

If you define size as volume, then if Mini-Me is 1/2 the height of Dr. Evil, perhaps he is also 1/2 the width and 1/2 the depth. Then he would be 1/2 * 1/2 * 1/2 which would actually be about “1/8 your size.”

Eventually you will be ready to show students this clip with what he says unbleeped:

 

If you’ve defined size as volume, then this answer will confirm your results.

If you’ve defined size as height, then watch students’ faces as they hear “Number 2” says he is “one eighth your size.”  Hopefully students will have moments of doubt but emerge confident that their answer is correct and that the movie got it wrong.  This is a great opportunity to “critique the reasoning of others.” (Math Practice 3)  Ask students “Why is your answer different from what they said in the movie?”  My guess is that it doesn’t sound very small to say “one half your size” so they made it sound a little better and said “one eighth your size” even though it wasn’t mathematically precise.

If you want, you can extend the problem by asking students:

• How tall would Mini-Me have to be if he really was one eighth of Dr. Evil’s size? (about 8.5 inches or 0.22 meters)
• How tall would Dr. Evil have to be if Mini-Me really was one eighth his size? (about 21 feet, 3 inches or 6.48 meters)

 

Below are a high, medium, and two low work samples for the challenge.  Only focus on the “What is your conclusion?” part.  Note that high is very relative and could be much higher:

• High (Answer is correct and student explains why Number 2 is wrong.  Doesn’t really explain how she got 1/2 though)

• Medium (Does not list the actual fraction of height.  Student’s explanation shows some sense making but is not very strong)

• Low (No answer is given. Explanation is more about calculations and less about what the calculations have to do with anything)

• Low (This one just made me laugh)

 

• CCSS 5.NF.5 Interpret multiplication as scaling (resizing)
• CCSS 5.NF.5a Comparing the size of a product to the size of one factor on the basis of the size of the other factor, without performing the indicated multiplication.
• CCSS 5.NF.5b Explaining why multiplying a given number by a fraction greater than 1 results in a product greater than the given number (recognizing multiplication by whole numbers greater than 1 as a familiar case); explaining why multiplying a given number by a fraction less than 1 results in a product smaller than the given number; and relating the principle of fraction equivalence a/b = (n × a)/(n × b) to the effect of multiplying a/b by 1.
• CCSS 6.NS.3 Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.

 

• Verne Troyer on IMDB
• Mike Myers on IMDB
  
• Austin Powers
• Movieclips.com