- How can you describe Ms. Pac-Man’s movements?
- What movement did Ms. Pac-Man make?
- What was the very first thing Ms. Pac-Man did?
- Does anyone have the same answer but a different way to explain it?
- How did you reach that conclusion?
- How can you demonstrate what you are saying is correct?
- What assumptions are you making?
Before going further, it’s important to explain an important misunderstanding I had with transformations. My friend Mark Goldstein pointed out and while I understand it now, I didn’t always, so let me try and explain. Essentially, when a transformation occurs, it is a mapping of the entire plane to the plane, not just a figure moving from one place to another. So, Ms. Pac-Man isn’t truly a representation of the three transformations we teach (translations, rotations, and reflections), but her movements remind us of them, because she slides, turns, and flips.
As for the lesson, I made assumptions about what students would say and have created animated videos to show the imprecision in students’ statement. Specifically, if you begin by showing students the video game movie clip above and ask them, “What movement did Ms. Pac-Man make?” my guess is that they will say that “Ms. Pac-Man first moved to the right, then up, then right, then …” What they are imprecisely describing are translations and you can help them “use clear definitions in discussion with others and in their own reasoning” (Math Practice 6) by telling them that “Mathematicians calls those types of movements translations.” Then show them the video below:
You may need to switch back and forth between the original video and this new video to compare the two sets of movements. What I hope they realize is that while it is true that Ms. Pac-Man translated across the screen (we will discuss this in more precise terms later), that was not the only movement Ms. Pac-Man made. Ask them “What was the next thing Ms. Pac-Man did?” and expect to hear answers like “She looked the other way” or “She turned to the right.” Again you can tell them that “Mathematicians call those types of movements reflections.” Then show them the video below (NOTE: YouTube cut off the first second so if may look like Ms. Pac-Man begins reflected even though she doesn’t):
Again, you may need to switch back and forth between the original video and this new video to compare the two sets of movements. Something important to note is that when Ms. Pac-Man gets to the top right of the screen, she starts doing both rotations and reflections where as in the beginning she is only doing one transformation at a time. In the video below I am only showing translations and reflections (no rotations) so she does one reflection at the very beginning and another towards the top right of the screen.
At this point they will most likely realize that Ms. Pac-Man turns in addition to the other movements. Similarly you can tell students that “Mathematicians call those types of movements rotations.” Then show them the video below:
By now students will realize that Ms. Pac-Man is making a series of translations, reflections, and rotations but we need to increase our mathematical precision and list them out. To help students realize this lack of precision ask them questions which should illustrate our communication problem like:
- How far did she translate?
- What unit are we measuring this in?
- Which way did she reflect?
- How much did she rotate?
Hopefully students will realize that to answer these questions (and at least the first one) we will need a common unit of measure. Students may something like, “She moved up 5 dots ” but what about in the beginning where there are no dots? When students are realizing they need some structure to have a meaningful conversation, show them the video below:
Have students to create a list of these movements on a sheet of paper. You will likely have to play the clip above many times and also give them printed copies of the images below. The grid helps give them the coordinates and the two Ms. Pac-Man pictures are very helpful in demonstrating the rotation/reflection combinations:
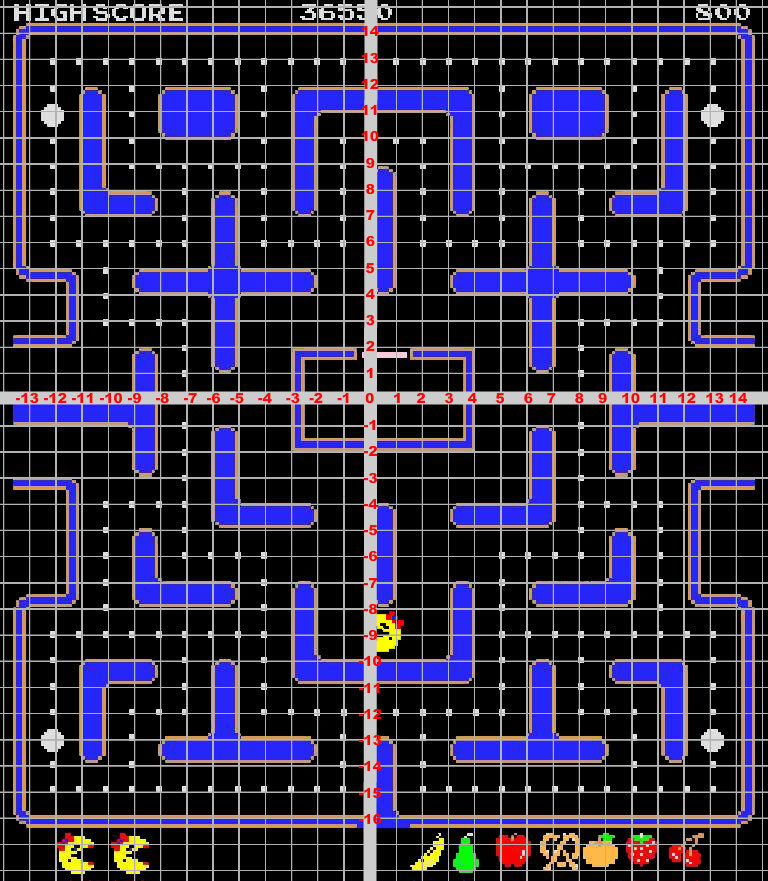


Once students have come up with their list of transformations, have a conversation about them as students may have incorrect answers, a different right answer, or multiple ways to explain it. These questions may be especially useful:
- Does anyone have the same answer but a different way to explain it?
- How did you reach that conclusion?
- How can you demonstrate what you are saying is correct?
- What assumptions are you making?
I went through the video and made my own list of transformations. Here is what I have (included as a PDF in the “Download files” link):
- Start at (0.5, -9)
- Reflection across line x = 0.5
- Translation 1.5 units right to (2, -9)
- Rotation 90° counterclockwise
- Translation 3 units up to (2, -6)
- Rotation 90° clockwise
- Translation 6 units right to (8, -6)
- Rotation 90° counterclockwise
- Translation 9 units up to (8, 3)
- Rotation 90° clockwise
- Translation 3 units right to (11, 3)
- Rotation 90° counterclockwise
- Translation 3 units up to (11, 6)
- Two possibilities (UP THEN LEFT)
- Reflection across line x = 11 AND Rotation 90° counterclockwise
- Rotation 90° clockwise AND Reflection across line x = 11
- Translation 3 units left to (8, 6)
- Two possibilities (LEFT THEN UP)
- Reflection across line x = 8 AND Rotation 90° counterclockwise
- Rotation 90° clockwise AND Reflection across line x = 8
- Translation 3 units up to (8, 9)
- Two possibilities (UP THEN LEFT)
- Reflection across line x = 8 AND Rotation 90° counterclockwise
- Rotation 90° clockwise AND Reflection across line x = 8
- Translation 3 units left to (5, 9)
- Two possibilities (LEFT THEN DOWN)
- Reflection across line x = 5 AND Rotation 90° clockwise
- Rotation 90° counterclockwise AND Reflection across line x = 5
- Translation 3 units down to (5, 6)
- Two possibilities (DOWN THEN LEFT)
- Reflection across line x = 5 AND Rotation 90° clockwise
- Rotation 90° counterclockwise AND Reflection across line x = 5
- Translation 3 units left to (2, 6)
- Two possibilities (LEFT THEN UP)
- Reflection across line x = 2 AND Rotation 90° counterclockwise
- Rotation 90° clockwise AND Reflection across line x = 2
- Translation 4 units up to (2, 10)
- Two possibilities (UP THEN LEFT)
- Reflection across line x = 2 AND Rotation 90° counterclockwise
- Rotation 90° clockwise AND Reflection across line x = 2
- Translation 3 units left to (-1, 10)
- Two possibilities (LEFT THEN DOWN)
- Reflection across line x = -1 AND Rotation 90° clockwise
- Rotation 90° counterclockwise AND Reflection across line x = -1
- Translation 4 units down to (-1, 6)
- Two possibilities (DOWN THEN LEFT)
- Reflection across line x = -1 AND Rotation 90° clockwise
- Rotation 90° counterclockwise AND Reflection across line x = -1
- Translation 3 units left to (-4, 6)
- Two possibilities (LEFT THEN UP)
- Reflection across line x = -4 AND Rotation 90° counterclockwise
- Rotation 90° clockwise AND Reflection across line x = -4
- Translation 3 units up to (-4, 9)
- Two possibilities (UP THEN LEFT)
- Reflection across line x = -4 AND Rotation 90° counterclockwise
- Rotation 90° clockwise AND Reflection across line x = -4
- Translation 5 units left to (-9, 9)
To be honest, it got much trickier for me starting with Transformation #14. I had to make Ms. Pac-Man drawings and prove to myself that what I wrote down was correct. It is certainly easy to get mixed up as this requires strong visual/spatial skills.
A few notes:
- I initially put the ALL CAPS phrases in when I started noticing a pattern in the transformations. I intended on deleting them but ultimately decided to keep them in as they might be helpful to you.
- I listed “Two possibilities” but technically there are infinite possibilities:
- You could add multiples of 360° to the rotation (so instead of 90° you could have 450°) and that would take you to the same place.
- Also, rotating 90° in one direction is the same as rotating 270° in the other direction.
- Brian Miller shares his own take on implementing this task with his students and how they created a game board. Read about it here. He has since updated his implementation and you read about the tweaks here.
- Read about how Chase Orton implemented this lesson while working with a teacher he coaches. He includes modifications they made as well as the teacher’s reflections on the experience.
- Here’s a blog post from Annie Forest talking about how she implemented the lesson with her students prior to Hour of Code.
- Deb Boden incorporated both my lesson and Brian’s modification to make it her own and wrote about the results here.
- Here’s how Jenise Sexton worked through the problem with her students including a reference to the Pixels movie where Pac-Man was dilated.
- Holler combined my plans and Brian Miller’s to make a two-day version of the lesson where students can earn points via correct transformations which are verified by classmates.
- Jac Richardson shares her take on the problem and how “[she] didn’t even have to teach it! [Her] kids caught on so quickly they were describing multiple transformations like it was nothing!”
- Ben Winter shared how he incorporated this lesson into Google Slides and included a competitive element with fruits of different values.
- Kandace McCoy built upon John Rowe’s work to create this Desmos Actitivy Builder version of the lesson.
- CCSS 8.G.1 Verify experimentally the properties of rotations, reflections, and translations.
- CCSS 8.G.2 Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them.
- CCSS 8.G.3 Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates.
- CCSS 8.G.4 Understand that a two-dimensional figure is similar to another if the second can be obtained from the first by a sequence of rotations, reflections, translations, and dilations; given two similar two-dimensional figures, describe a sequence that exhibits the similarity between them.
- CCSS G-SRT.2 Given two figures, use the definition of similarity in terms of similarity transformations to decide if they are similar; explain using similarity transformations the meaning of similarity for triangles as the equality of all corresponding pairs of angles and the proportionality of all corresponding pairs of sides.
- CCSS G-CO.4 Develop definitions of rotations, reflections, and translations in terms of angles, circles, perpendicular lines, parallel lines, and line segments.
- CCSS G-CO.5 Given a geometric figure and a rotation, reflection, or translation, draw the transformed figure using, e.g., graph paper, tracing paper, or geometry software. Specify a sequence of transformations that will carry a given figure onto another.
- CCSS G-CO.6 Use geometric descriptions of rigid motions to transform figures and to predict the effect of a given rigid motion on a given figure; given two figures, use the definition of congruence in terms of rigid motions to decide if they are congruent.
- CCSS G-CO.7 Use the definition of congruence in terms of rigid motions to show that two triangles are congruent if and only if corresponding pairs of sides and corresponding pairs of angles are congruent.



Hi my name is Mike Ruhl and I am currently a senior at the University of Illinois studying to become a Mathematics teacher for Secondary Education. I really enjoyed how you took a common game like “Ms. Pac Man” and made the students think about the mathematical implications they may have not though about before. However, one concern I have with this activity is what to do if you have a student not know what Pac Man is ? Could this cultural context throw some students off and if so how could this lesson be adapted to accommodated for their misunderstandings?
I haven’t experienced that problem at all. Students have either heard of Ms. Pac-Man or get the idea very quickly.
I tried this, and actually turned my classroom into a coordinate plane and we played a real-life Pacman game. The kids had a lot of fun with it!
Please tell me that you took pictures and/or blogged about it!
How do you do this? What are the rules and expectations?
Thank you so much for this resource. It adapted to fit my lesson but it made the lesson so interesting and challenging.
Glad you liked it. It’s one of my favorite lessons to use.
Really enjoyed reading the activity. I am about to use it in a transfer task at school next week (skills of coordinates, and transformations including rotation, reflection and translation).
I teach in a 5 form entry Year 5 British international school in Malaysia.
We have amended it to include a competitive element using different valued fruits. See link below for teaching slides and student slides.
https://sites.google.com/view/teachingthelatest/shape-and-space/position-and-direction
Thanks for sharing this Ben! I’ve added it to the lesson above in the “Teacher Work” section.
I would like to note that many of the 8-bit and 16-bit games (like Mrs. Pacman) had sprite layers for different sections of the animation. For example, Mrs. Pacman would get her own sprite layer, the background would have its own sprite layer, and so on. This means that in many or most cases, changes to an individual layer would actually be a rigid transformation of the entire plane (sprite layer) to another instance of itself with some minor changes made by calculations prior to the redraw.
That said, when animations change in addition to sprite layer transformations, this can change things a bit. but the general idea is more correct than you may have thought!
Thanks Josh. This lesson certainly simplifies things more than they actually are, and your explanation is appreciated.
Hi Robert
This looks fantastic, I can’t wait to try it with my class this week.
I made up an A3 worksheet to match Ben’s challenge, so I thought I should add to all of the wonderful sharing that’s happening here!
It has a copy of the maze with the coordinates so students can manually explore their options, and the points key. You’d only need to print x2 of page #2 as there’s more than enough little Ms Pacman and her reflection for all students to have duplicates in one class.
https://drive.google.com/file/d/1snEpwJA9q41TEEvP3DwsWCQMs-w0Sg5d/view?usp=sharing
Thanks again and all the best!
Thank you for sharing this, Leah. That’s very kind of you. We’re better together.