
With that as a reference, watch this video:
- How much shorter are 20 layers of staggered pipe stacks?
- How much shorter are n layers of staggered pipe stacks?
- What information do we need to figure this out?
- What assumptions are we making?
- How can we figure out the stacks’ height if we don’t know the pipes’ radius?
This problem uses a combination of Algebra and Geometry. In particular, students need to realize that the centers of three stacked pipe circles form an equilateral triangle. The sides of this triangle are two radii long. The question then turns to how to find the height of that triangle. That can be done in multiple ways including the Pythagorean Theorem or trigonometric ratios as it forms a 30/60/90 triangle.
The context also provides a great opportunity to use multiple representations to express their answers. In particular, each additional row adds √3r to the height of the staggered pipe stack. It is critical that students are able to articulate why and where that is. To give you an idea of what this might look like, below is an example of how students might explain the height of the staggered pipe stack.

Students will need to know information about the diameter of the pipes in the video. I measured the diameter at 5.6 cm. Here are two pictures to help them out:


I hope that students will create a function to find the answer to these questions. Here is the answer I got for n layers and I will use it to find the answer to 20 layers. Assuming same number of layers and pipes of the same diameter:
n = number of layers
r = pipe’s radius
height difference = height of non-staggered pipes – height of staggered pipes
h = 2rn – (r + (n-1)(√3r) + r)
h = 2rn – (2r + (n-1)(√3r))
h = 2rn – 2r – (n-1)(√3r))
h = 2r(n – 1) – (n-1)(√3r))
h = (n – 1)(2r – √3r)
This is a great opportunity to use Math Practice 2 and contextualize the answer. The (n-1) is one less than the total number of layers as demonstrated by the picture. However, what does the (2r – √3r)? It defines the amount of pipe that goes down and between the pipes. The image below illustrates the two r’s and the √3r that is taken away.
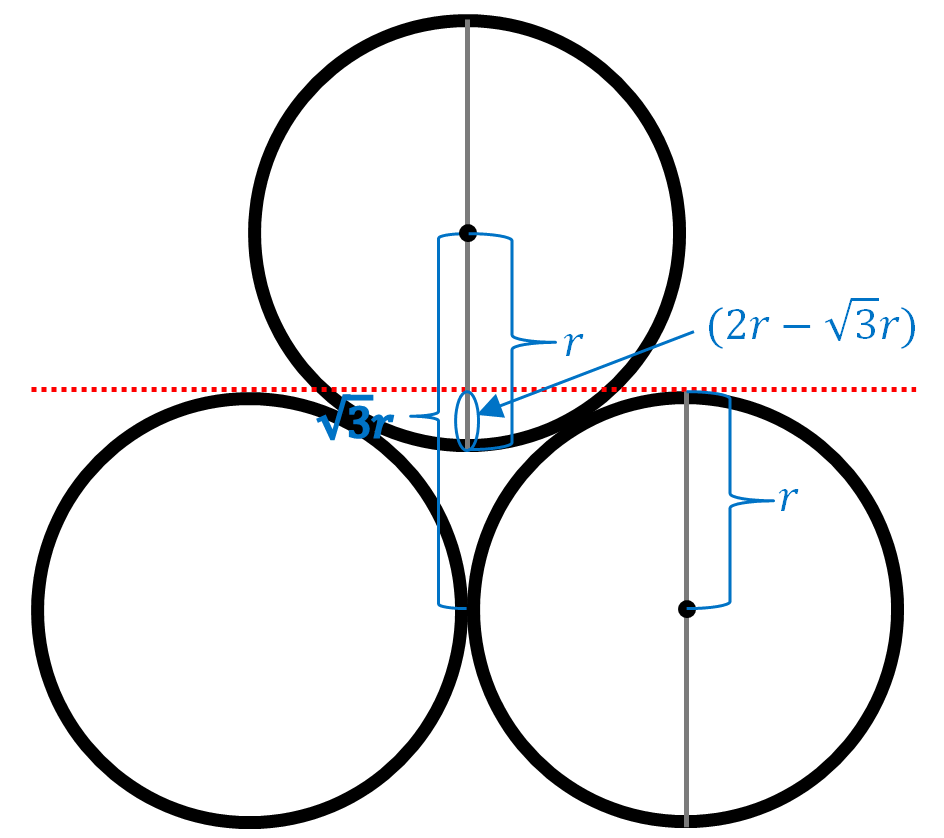
Taking it a little further you get the work below. So what does the ~0.27 represent? It represents the ~27% of the radius that goes down and between the pipes. Looking at the picture above, you can see that a little more than a fourth of the radius is below the red dotted line.
h = r(n – 1)(2 – √3)
h ≈ 0.27(r)(n-1)
I should mention that when I first did this problem, I had trouble interpreting what the ~0.27 represented. I thought it represented ~0.27 of the pipe’s height (or diameter). That would mean that about one fourth of the pipe dipped down and between the other pipes. That just didn’t seem reasonable. Thankfully my colleague Dalyn Miller-Geiser had the wonderful suggestion of trying it out with sections of a paper towel roll. Doing it that way, I realized that it was definitely not possible to be one fourth of the diameter but actually one fourth of the radius. That meant it was about one eighth of the pipe’s height which was much more reasonable. This is what it looked like.

Clearly they aren’t perfectly cylindrical, but they are a great manipulative to use if your students need them.
So, using this formula, 20 layers, and a diameter of 5.6 cm for the pipes I get:
h = r(n – 1)(2 – √3)
h = 2.8(20 – 1)(2 – √3) cm
h ≈ 14.255 cm
Now watch the video below that shows the answer to how much shorter staggered pipe stacks are at 20 layers.
Here is a closeup of the ruler:

As you can see, the theoretical answer of 14.255 cm was pretty close to the experimental answer I got which was near 14.6 cm. Sources of error may include:
- Bad measuring
- Bad ruler placement
- Pipes that are not stacked compactly
- Crooked stacks
Even with the small margin of error, the video help the students feel validated.
- CCSS 8.G.7 Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.
- CCSS A-CED.1 Create equations and inequalities in one variable and use them to solve problems. Include equations arising from linear and quadratic functions, and simple rational and exponential functions.
- CCSS A-CED.3 Represent constraints by equations or inequalities, and by systems of equations and/or inequalities, and interpret solutions as viable or nonviable options in a modeling context. For example, represent inequalities describing nutritional and cost constraints on combinations of different foods.
- CCSS A-CED.4 Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations. For example, rearrange Ohm’s law V = IR to highlight resistance R.
- CCSS A-SSE.1 Interpret expressions that represent a quantity in terms of its context.
- CCSS A-SSE.1a Interpret parts of an expression, such as terms, factors, and coefficients.
- CCSS A-SSE.1b Interpret complicated expressions by viewing one or more of their parts as a single entity. For example, interpret P(1+r)n as the product of P and a factor not depending on P.
- CCSS A-SSE.3 Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity represented by the expression.
- CCSS F-BF.1 Write a function that describes a relationship between two quantities.
- CCSS F-BF.1a Determine an explicit expression, a recursive process, or steps for calculation from a context.
- CCSS F-LE.2 Construct linear and exponential functions, including arithmetic and geometric sequences, given a graph, a description of a relationship, or two input-output pairs (include reading these from a table).
- CCSS F-LE.5 Interpret the parameters in a linear or exponential function in terms of a context.
- CCSS G-SRT.8 Use trigonometric ratios and the Pythagorean Theorem to solve right triangles in applied problems.
- CCSS G-MG.3 Apply geometric methods to solve design problems (e.g., designing an object or structure to satisfy physical constraints or minimize cost; working with typographic grid systems based on ratios).
- Image credit: dbvirago / 123RF Stock Photo



It would be interesting to extend to how much space is saved by staggering the pipes but keeping the same number of pipes being contained. Staggering loses one pipe contained every other layer. Would there even be a height savings once those other pipes are added to the staggered stack? Or maybe how many pipes wide would the bottom row have to be for there to be a height savings for m pipes?
That’s a really neat extension Jeffrey! I like it! Definitely let me know if you try it out and thanks for sharing.
Thank you for this lesson. I have a follow-up question. Your example assumes that the pipes are closely stacked with no gaps. What would the calculation be if the bottom layer of pipes were 1″ apart (not touching) How would you determine the height of a stack with only two layers
Thanks Ray. What strategies have you already tried?
What is really interesting, is that in your example, while there is a drop in height for the staggered stack ‘per layer’ the volume of pipe held is actually less. This means that due to the wasted space on the outside of every other layer your stack would actually be higher if you had the same amount of pipes.
There would need to be another adjustment to calculate when you would be saving height dependent on the width of the stack (how many pipes wide). I only bring this up as I am currently designing racks for a plumbing retail store and they want to maximize the amount of pipe they can fit in a given area. Having thin tall racks is obviously not the answer to their problem. Hmmm…. great food for thought.
Thanks Bob. You’re definitely focusing on a more practical implementation of this problem. In your situation, it sounds like maximizing the quantity of pipes is much more important than minimizing the height of the stack of pipes.
So if the height saved per layer is 27% of r, then it would be 13.5% of d, so you save a layer of height every 100/13.5=7.4 layers. In those 7.4 layers you have lost at most 7.4/2 pipes of capacity (you lose one pipe every other layer). Let where n is the number of pipes in the lowest (larger) level. Your best case scenario is that you get to add an extra layer of n with a worst case scenario being the n-1 case. So if n-1>7.4/2, or n>4.7, then it is more efficient to layer offset, otherwise stack normally. Right? This fits your case of n=3.
If I understand you correctly, you are using a proportional reasoning strategy. That is a very common way to approach it. The problem comes in with the layers and it’s hard to visualize in text. For example, if you find the height difference of 5 layers, and then do 4 of that, there will be gaps between the four sets of layers that are non-staggers, Depending on how many of those there are, the margin of error will increase.
I think this is a really great activity and I think students would enjoy it!
Hi Robert,
What a great task!
Do you have a way to assess the outcomes?
Do you use observation or more formal assessment such as a marking criteria or rubric?
If so, would you be willing to share it too?
Thanks Angela. You’ll like this blog post to answer your questions: https://robertkaplinsky.com/4-ways-assess-3-act-tasks/
I like this activity as it forces students to think of ways to solve. They may begin to wonder things and ask questions of each other and the teacher. For example as one participant has already mentioned, the amount of space for the same number of pipes as you lose one pipe in every other row with the staggered pipes. Students may wonder are you actually saving space if you need to keep the same number of pipes. These are the questions that I may right out as I put my student hat on while planning.
Great perspective, TaJuana. This is one of the most rigorous math problems I have on my website, and it certainly can get people noticing and wondering. Lots of approaches too (for example Pythagorean Theorem vs trig ratios). Thanks for checking in.