Download
The Situation
The Challenge(s)
- How many calories is one _____________?
- How many ___________ could you eat if you only wanted to eat exactly ________ calories? (one-step equation)
- How many ___________ could you eat if you only wanted to eat at most ________ calories? (one-step inequality)
- How many more _________ could you eat if you have already eaten ______ of them and want to only eat exactly _______ calories? (two-step equation)
- How many more _________ could you eat if you have already eaten ______ of them and want to eat at most _______ calories? (two-step inequality)
Question(s) To Ask
- What is a guess that is too low?
- What is a guess that is too high?
- What is your best guess?
Consider This
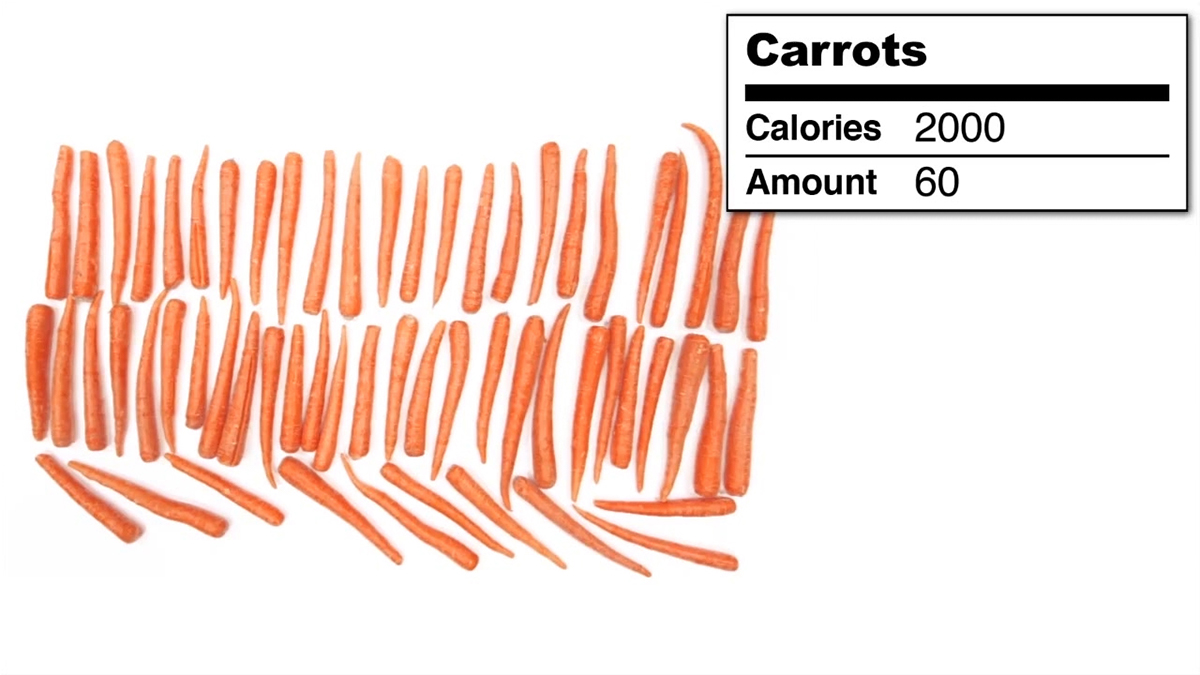
This problem uses a visual representation of what 2,000 calories looks like as a context for unit rates and solving one- and two-step equations / inequalities. As an example, using “Food 1” (under “What You’ll Need) below:
- How many calories is one bagel?
- How many bagels could you eat if you only wanted to consume 2500 calories?
- How many more bagels could you eat if you have already eaten 4 of them and want to only eat exactly 2200 calories?
- How many more bagels could you eat if you have already eaten 2 of them and want to eat at most 2100 calories?
You will notice that some foods do not neatly tally up to 2000 calories so you can assign different foods accordingly.
One last thing to consider when doing this problem was brought up by Lucam Chups and is shown below:
What You'll Need
- Food 1
- Food 2
- Food 3
- Food 4
- Food 5
- Food 6
- Food 7
- Food 8
- Food 9
- Food 10
- Food 11
- Food 12
- Food 13
- Food 14
- Food 15
- Food 16
- Food 17
- Food 18
- Food 19
- Food 20
- Food 21
- Food 22
- Food 23
- Food 24
Teacher Work
Check out Merryl Polak’s implementation of this lesson with her seventh grade students and her reflections on how it went.
Content Standard(s)
-
Various state nutrition standards including seventh and eighth grade California 1.6.N – Analyze the caloric and nutritional value of foods and beverages.
-
CCSS 6.EE.3 – Apply the properties of operations to generate equivalent expressions. For example, apply the distributive property to the expression 3 (2 + x) to produce the equivalent expression 6 + 3x; apply the distributive property to the expression 24x + 18y to produce the equivalent expression 6 (4x + 3y); apply properties of operations to y + y + y to produce the equivalent expression 3y.
-
CCSS 6.EE.4 – Identify when two expressions are equivalent (i.e., when the two expressions name the same number regardless of which value is substituted into them). For example, the expressions y + y + y and 3y are equivalent because they name the same number regardless of which number y stands for.
-
CCSS 6.EE.5 – Understand solving an equation or inequality as a process of answering a question: which values from a specified set, if any, make the equation or inequality true? Use substitution to determine whether a given number in a specified set makes an equation or inequality true.
-
CCSS 6.EE.6 – Use variables to represent numbers and write expressions when solving a real-world or mathematical problem; understand that a variable can represent an unknown number, or, depending on the purpose at hand, any number in a specified set.
-
CCSS 6.EE.7 – Solve real-world and mathematical problems by writing and solving equations of the form x + p = q and px =q for cases in which p, q and x are all nonnegative rational numbers.
-
CCSS 6.EE.8 – Write an inequality of the form x > c or x < c to represent a constraint or condition in a real-world or mathematical problem. Recognize that inequalities of the form x > c or x < c have infinitely many solutions; represent solutions of such inequalities on number line diagrams.
-
CCSS 6.RP.2 – Understand the concept of a unit rate a/b associated with a ratio a:b with b ≠ 0, and use rate language in the context of a ratio relationship. For example, “This recipe has a ratio of 3 cups of flour to 4 cups of sugar, so there is 3/4 cup of flour for each cup of sugar.” “We paid $75 for 15 hamburgers, which is a rate of $5 per hamburger.”1
- CCSS 6.RP.3 – Use ratio and rate reasoning to solve real-world and mathematical problems, e.g., by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations.
- CCSS 6.RP.3b – Solve unit rate problems including those involving unit pricing and constant speed. For example, if it took 7 hours to mow 4 lawns, then at that rate, how many lawns could be mowed in 35 hours? At what rate were lawns being mowed?
- CCSS 7.EE.1 – Apply properties of operations as strategies to add, subtract, factor, and expand linear expressions with rational coefficients.
-
CCSS 7.EE.4 – Use variables to represent quantities in a real-world or mathematical problem, and construct simple equations and inequalities to solve problems by reasoning about the quantities.
-
CCSS 7.EE.4a – Solve word problems leading to equations of the form px + q = r and p(x + q) = r, where p, q, and r are specific rational numbers. Solve equations of these forms fluently. Compare an algebraic solution to an arithmetic solution, identifying the sequence of the operations used in each approach. For example, the perimeter of a rectangle is 54 cm. Its length is 6 cm. What is its width?
-
CCSS 7.EE.4b – Solve word problems leading to inequalities of the form px + q > r or px + q < r, where p, q, and r are specific rational numbers. Graph the solution set of the inequality and interpret it in the context of the problem. For example: As a salesperson, you are paid $50 per week plus $3 per sale. This week you want your pay to be at least $100. Write an inequality for the number of sales you need to make, and describe the solutions
Source(s)
Download



























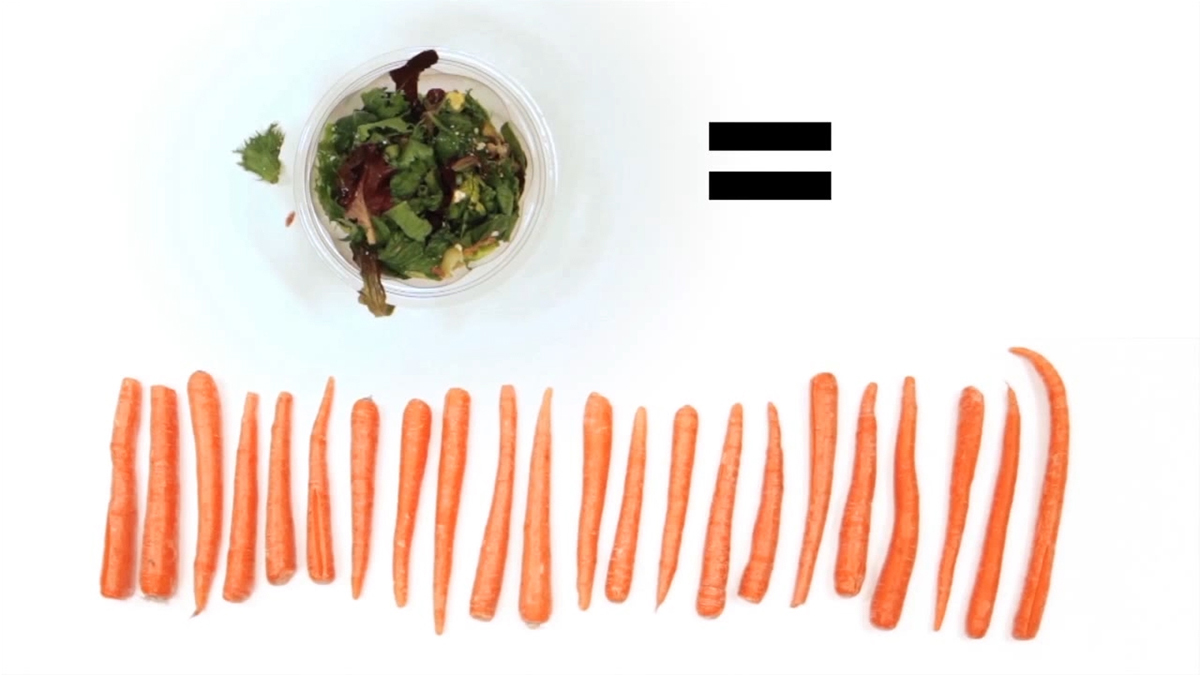
Please be cautious of students who may have disordered eating (anorexia, bullemia, binge eating disorder, EDNOS). This could be a very triggering lab that may damage their mental health.
Wow Kayla. Thanks for this heads up. This never crossed my mind but is certainly something for teachers to be aware of. Much appreciated.
My daughter’s swim coach just talked to them about nutritional planning. I can’t wait to share this awesome video and lesson. They are thinking along those lines anyway…food, folks, fun, swimming and math! The best of so many worlds. Thank you for expanding the way we think.
Isn’t it great when that happens. Obviously, as Kayla mentioned, there is more to nutrition than simply adding and subtracting calories, but it’s definitely a conversation point.
I apologize for going off topic, but we see the Mcdonald’s, Dunkin Donuts, Chipotle, Entemanns and Coke letters used in the opening of the video, but where do all the other letters come from?
Sorry Phillip. Not sure.
This lesson needs to be removed. Eating disorders are up 75%. Students shouldn’t have to be triggered in math class.
This lesson address many states’ standards including California 1.6.N – Analyze the caloric and nutritional value of foods and beverages.