Do We Have Enough Paint?

Your class wants to paint one side of the handball wall below.  You already have one full can of paint.

• How can we figure out if we have enough paint?
• Do we have enough paint?
• Do we have enough paint for a second coat?

These questions may be useful in helping students down the problem solving path:

• What information do we need to know to answer this question?
• Can you make a drawing or model to represent your answer?
• Where are the 7 feet in your drawing/model?
• Where are the 10 feet in your drawing/model?
• Where are the 70 square feet in your drawing/model?
• How long does each side of the square represent?
• Does anyone else have the same answer but another way to explain it?

This lesson was created together with five fantastic teachers from Downey Unified School District as part of a lesson study.  Our goal was to provide a context for students to conceptually understand area including the differences between linear and square units.  We initially began with the challenge question of “Do we have enough paint to paint the handball wall?”  What we found was that students answered with “yes” or “no” responses without really thinking about the question.  In the second lesson we decided to change the question so that students could not respond with a “yes” or “no” and were forced to respond with a more elaborate answer that they had to think about.

As students ponder whether they can figure out if they have enough paint, they eventually must realize that they need more information to come to a conclusion.  You can help them, if needed, by asking “What information do we need to know to answer this question?”  Eventually they will need to know the handball wall’s dimensions and the paint’s coverage area.

Below is the handball wall with superimposed dimensions.  Note that we never actually measured the wall’s dimensions and are using rough estimates.

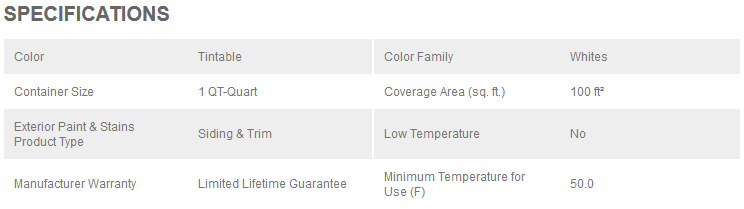
Here is a picture of the paint can with information about its coverage area.  We are assuming (unrealistically) that no paint is left in the can or wasted on the brush.  Note that you should be careful about how you talk about the paint.  It has the potential to be misleading for kids because paint is sold by the volume but we measure it in terms of what area it will cover.  So, saying something like “this paint can holds 100 square feet of paint” is misleading.  Really it should be “the paint in this can covers an area of 100 square feet.”

Once students have this information, let them explore the question.  Consider providing tools such as rulers, square tiles (pictured below), or other resources to help them make sense of the problem.  We also gave students a 7 inch by 10 inch rectangle printed (included in “Download files” button) on a paper to represent the wall, but that seemed to both help some students and create potential misunderstandings in others.

Keep in mind that while some students may immediately realize that you can multiply 7 feet and 10 feet to get 70 square feet, which is less than 100 square feet, this may be a superficial understanding.  For example, in the picture above, the student with the yellow tiles is making a 7 by 10 rectangle.  However, the student with the blue tiles is making an 8 by 12 rectangle.  What do they understand right now?

Challenge students with these questions and consider how the two students above might answer:

• Can you make a drawing or model to represent your answer?
• Where are the 7 feet in your drawing/model?
• Where are the 10 feet in your drawing/model?
• Where are the 70 square feet in your drawing/model?
• How long does each side of the square represent?

When discussing the results, make sure students understand where the 7 and 10 feet are (linear units) and where the 70 square feet of paint (square units) are.  To encourage deeper conversations, the question “Does anyone else have the same answer but another way to explain it?” may be useful.  Ultimately students should conclude that the wall requires 70 square feet of paint and since the paint we already have covers 100 square feet, we have enough.

The extension question asks whether we have enough to paint the wall with a second coat.  Students may need help understanding that this means painting it completely twice.  Since that would require 140 square feet of coverage, we do not have enough paint for a second coat.

Below are two low, medium, and high work samples for both the main challenge and the extension along with comments explaining how I classified it:

• Main challenge – Low (Correct answer but explanation is incoherent)

• Main challenge – Low (Correct answer but explanation is incoherent)

• Main challenge – Medium (Correct answer and decent explanation but missing some units)

• Main challenge – Medium (Correct answer and decent explanation but missing units)

• Main challenge – High (Correct answer and strong explanation)

• Main challenge – High (Correct answer and strong explanation)

• Extension – Low (Incorrect answer with incoherent explanation)

• Extension – Low (Correct answer with incoherent explanation)

• Extension – Lower Medium (Correct answer with incoherent explanation)

• Extension – Medium (Correct answer with explanation that is missing units and has calculation errors)

• Extension – High (Correct answer with strong explanation.  Unit usage could be slightly better)

• Extension – High (Correct answer with strong explanation)

• CCSS 3.MD.5 Recognize area as an attribute of plane figures and understand concepts of area measurement.
• CCSS 3.MD.5a A square with side length 1 unit, called “a unit square,” is said to have “one square unit” of area, and can be used to measure area.
• CCSS 3.MD.5b A plane figure which can be covered without gaps or overlaps by n unit squares is said to have an area of n square units.
• CCSS 3.MD.6 Measure areas by counting unit squares (square cm, square m, square in, square ft, and improvised units).
• CCSS 3.MD.7 Relate area to the operations of multiplication and addition.
• CCSS 3.MD.7a Find the area of a rectangle with whole-number side lengths by tiling it, and show that the area is the same as would be found by multiplying the side lengths.
• CCSS 3.MD.7b Multiply side lengths to find areas of rectangles with whole-number side lengths in the context of solving real world and mathematical problems, and represent whole-number products as rectangular areas in mathematical reasoning.
• CCSS 3.MD.7c Use tiling to show in a concrete case that the area of a rectangle with whole-number side lengths a and b + c is the sum of a × b and a × c. Use area models to represent the distributive property in mathematical reasoning.
• CCSS 3.MD.7d Recognize area as additive. Find areas of rectilinear figures by decomposing them into non-overlapping rectangles and adding the areas of the non-overlapping parts, applying this technique to solve real world problems.

• Home Depot