How Much Did Peterson Lose By Not Cashing His Check?

 
NFL cornerback Patrick Peterson received a $15,361,000 signing bonus as part of a five-year, $70 million contract extension.  However, he didn’t immediately cash the check.  When asked why, he said, “I just haven’t gotten around to it.”
 

• How much interest money did Peterson lose by not immediately cashing his check?

 

These questions may be useful in helping students down the problem solving path:

• What is a guess that is too low?
• What is a guess that is too high?
• What is a guess that you know is wrong?
• What is your best guess?
• What information do we need to figure this out?
• How much money would he have lost if he took 3 months to deposit the check?
• How much money would he have lost if he took n months to deposit the check?

 

This context makes for an interesting application of calculating interest.  Normally we don’t think much about the interest we lose out on from not immediately cashing a check, but when the check is for over $15,000,000, it becomes noteworthy.  To determine the amount of interest money Peterson lost, students will need to know:

• the original amount of money
• the amount of time that passed between the date the check was issued and the date the check was deposited.
• the interest rate for the money could have earned had it been deposited.

 

The image below is a screen shot from Bleacher Report that provides some of the necessary information.

 

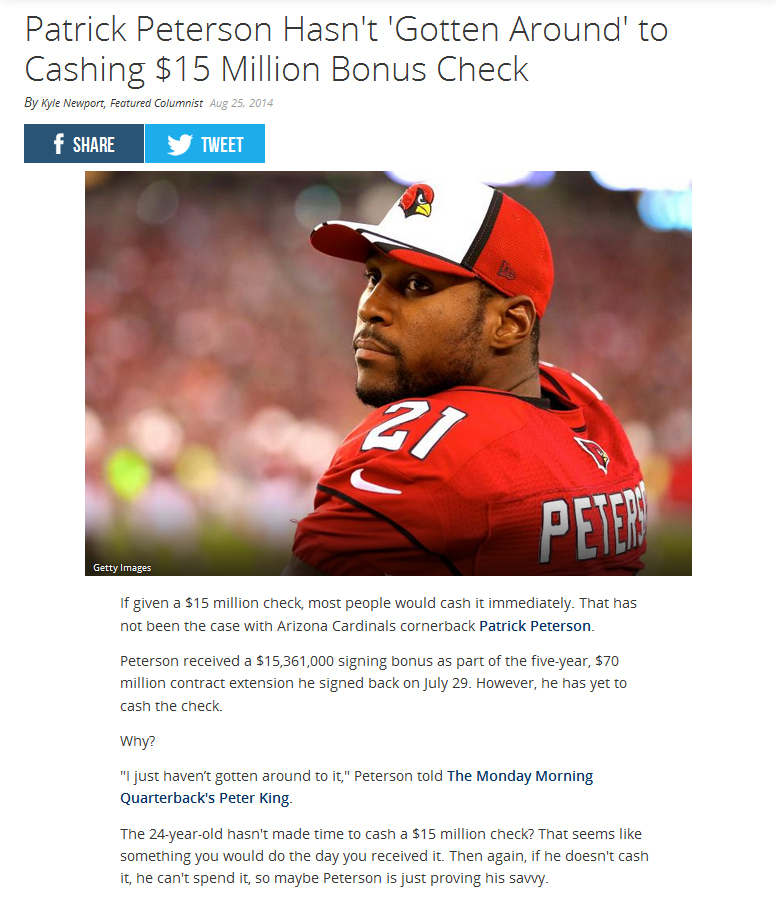
The check was written for $15,361,000 so that is the original amount of money.  Assuming that Peterson received the check on the date the contract was signed, he got it on July 29, 2014.  While we don’t know the exact date he cashed it, I believe that it was not cashed as of the day the story was written which was August 25, 2014.  There are 27 days from the date he received it to the date of the article.

 

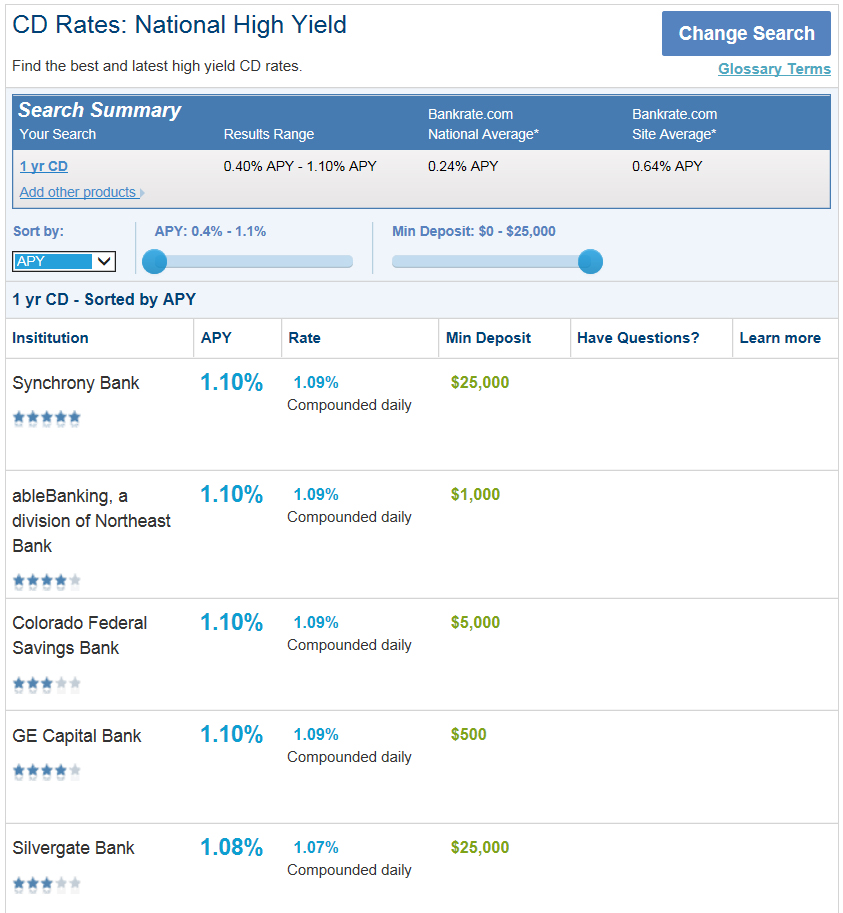
As for the interest rate, these were the rates available for certificates of deposit (CDs) in August 2014.  In general, CD interest rates are slightly higher than the rates earned from a savings or money market account.  They are usually lower than the rates you could earn through other means, such as stocks, but have little risk unless the bank goes out of business.  The best interest rates available were 1.1% compounded daily.

 

In terms of actually finding the amount of money Patrick Peterson lost by not depositing his check, I am using the formula of: A = p(1 + r/n) ^ (n * t) where p is the amount of principal, r is the rate, n is the # of times per year the amount is compounded, and t is the # of years.

• p = 15361000
• r = 1.1% or 0.011
• n = 365 for daily compounding
• t = 27/365 (fraction of the year it was compounded which is the # of days he waited to cash the check divided by 365 days per year)

 

This gives us a total of $15,373,504.12 which results in $12,504.12 in lost interest over the 27 days.  Now this amount does not include deductions for income tax but is still a staggering amount of money for 27 days of conservative interest.  If he had earned a more aggressive interest rate like 6%, the interest would have been over $68,000 for the same period of time!  I believe that if Patrick Peterson knew he could have earned enough money to buy a small car or go on a trip to anywhere in the world, he would have deposited the check sooner.

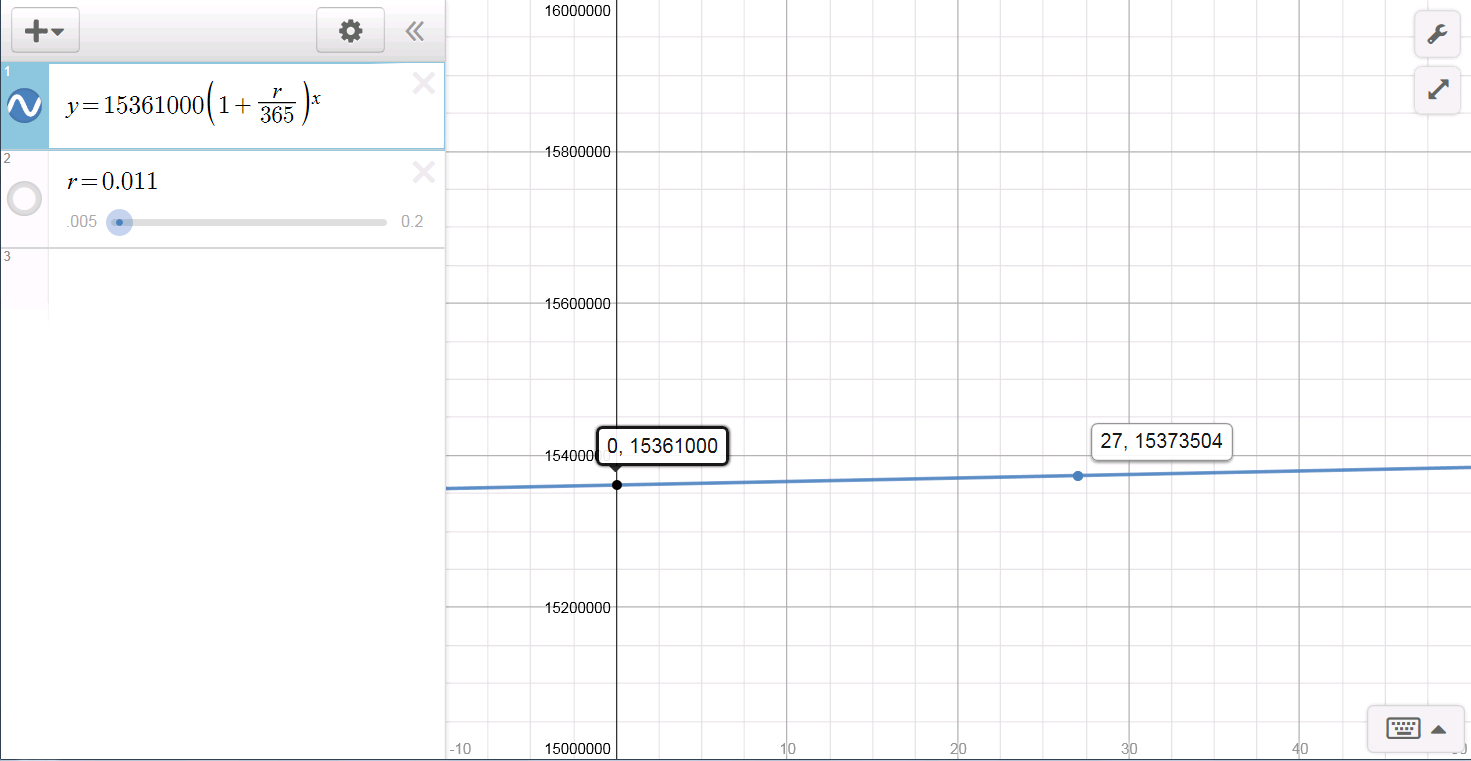
I have also made an interactive graphical version of this problem using Desmos with a slider for the rate.  It is fun to play around with the rate to see how things change.  The image below shows you a sneak preview with the amounts of money at day 0 and day 27.

 
Read about how Tina Palmer implemented this problem with her students.  She used the  Math Forum’s Powerful Problem Solvingstrategies to implement the problem to great success.
 

• CCSS 7.RP.3 Use proportional relationships to solve multistep ratio and percent problems. Examples: simple interest, tax, markups and markdowns, gratuities and commissions, fees, percent increase and decrease, percent error.
• CCSS N-RN.2 Rewrite expressions involving radicals and rational exponents using the properties of exponents.
• CCSS A-SSE.1 Interpret expressions that represent a quantity in terms of its context.^★
• CCSS A-SSE.3c Use the properties of exponents to transform expressions for exponential functions. For example the expression 1.15^t can be rewritten as (1.15^1/12)^12t ≈ 1.012^12t to reveal the approximate equivalent monthly interest rate if the annual rate is 15%.
• CCSS A-SSE.4 Derive the formula for the sum of a finite geometric series (when the common ratio is not 1), and use the formula to solve problems. For example, calculate mortgage payments.^★
• CCSS A-REI.11 Explain why the x-coordinates of the points where the graphs of the equations y = f(x) and y = g(x) intersect are the solutions of the equation f(x) = g(x); find the solutions approximately, e.g., using technology to graph the functions, make tables of values, or find successive approximations. Include cases where f(x) and/or g(x) are linear, polynomial, rational, absolute value, exponential, and logarithmic functions.^★
• CCSS F-IF.4 For a function that models a relationship between two quantities, interpret key features of graphs and tables in terms of the quantities, and sketch graphs showing key features given a verbal description of the relationship. Key features include: intercepts; intervals where the function is increasing, decreasing, positive, or negative; relative maximums and minimums; symmetries; end behavior; and periodicity.^★
• CCSS F-IF.7e Graph exponential and logarithmic functions, showing intercepts and end behavior, and trigonometric functions, showing period, midline, and amplitude.
• CCSS F-IF.8b Use the properties of exponents to interpret expressions for exponential functions. For example, identify percent rate of change in functions such as y = (1.02)t, y = (0.97)t, y = (1.01)12t, y = (1.2)t/10, and classify them as representing exponential growth or decay.
• CCSS F-BF.2 Write arithmetic and geometric sequences both recursively and with an explicit formula, use them to model situations, and translate between the two forms.^★
• CCSS F-LE.1c Recognize situations in which a quantity grows or decays by a constant percent rate per unit interval relative to another.
• CCSS F-LE.4 For exponential models, express as a logarithm the solution to ab^ct = d where a, c, and d are numbers and the base b is 2, 10, or e; evaluate the logarithm using technology.
• CCSS F-LE.5 Interpret the parameters in a linear or exponential function in terms of a context.

 

• Bleacher Report
• Bank Rate (rates as of August 2014)
• Desmos