Depth of Knowledge Matrix – 4th Grade

[Looking for other grade levels? The button below allows you to download all of them or you can look here.]
 
If you’ve been looking for a way to challenge your students that was simultaneously accessible for all students but still challenged your high flyers, then you’ll love the problems on my Open Middle Depth of Knowledge matrix. I’ll be releasing each grade level separately but if you want to see all of them now, you can download high quality, printable PDFs by clicking the button below.

It includes:

• Elementary & Secondary matrix (a selection from 8 grade levels)
• Elementary matrix (kindergarten through 5th)
• Secondary matrix (6th grade through calculus)
• 3rd, 4th, 5th, 6th, 7th, 8th, Algebra 1, Geometry, and Algebra 2 matrices (separate matrices for each grade level)

 

The pictures below give you a preview of what the front and back of the matrix looks like.  Each column explores one of eight topics: fractions on a number line, comparing fractions, adding mixed numbers, comparing decimals, adding multiples, multiplying differences, multi-digit division, and patterns.

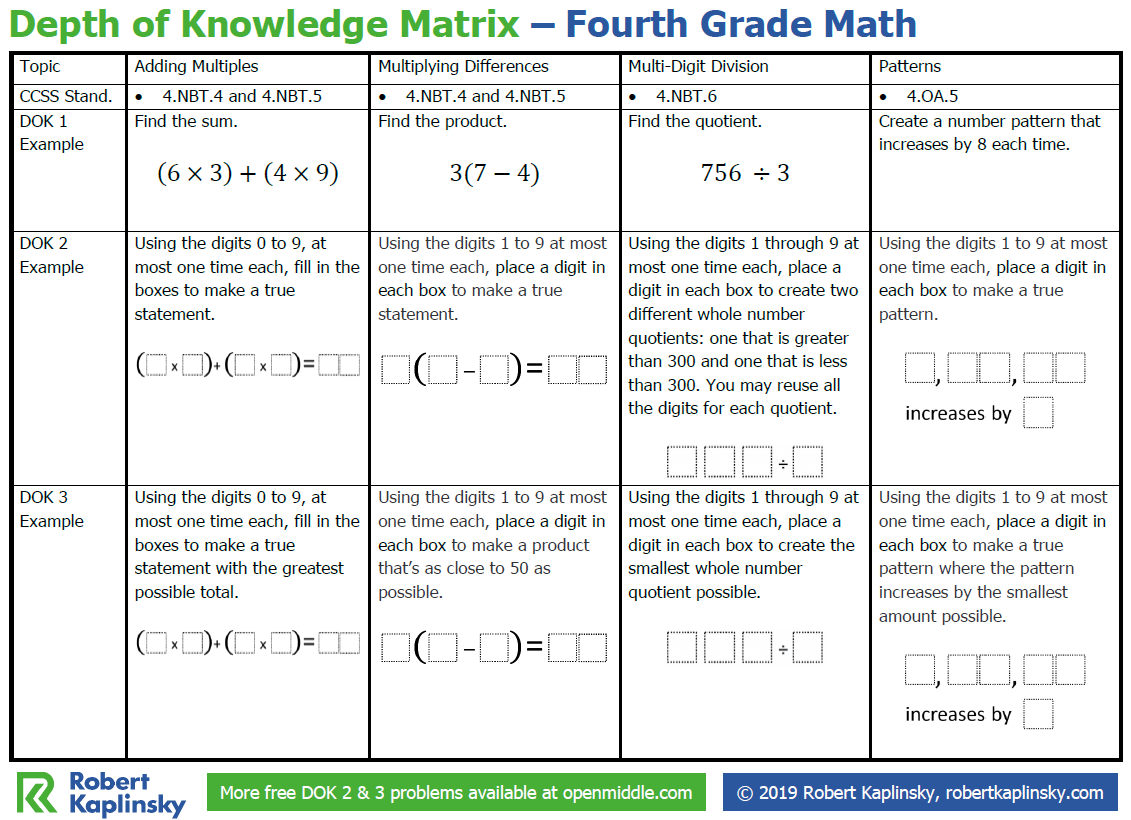
You’ll notice that the first problem in the column is traditional and familiar. It’s something you’d expect students in your class to eventually be able to figure out. Then look at the Open Middle problems at DOK 2 and DOK 3. You’ll notice that they’re on the same topic, yet are significantly more challenging. You may start to wonder whether or not your students can solve them, and what that may imply about how well they understand the concept.

 

 

 

If you like these Open Middle problems and want to see the answers (I’m still working on getting them uploaded) or want to find more DOK 2 and DOK 3 problems, check out openmiddle.com.  Open Middle is a collaborative website where all problems are free and new submissions are welcome.  The more problems people submit, the more problems we all have access to.

 

If you’re looking for more support with implementing Open Middle problems in your classroom, I’ve got three options for you to consider:

• I’ve recorded a free webinar with versions for elementary (K-5) and secondary (6-12) math teachers called Why We Should Reconsider Using Worksheets (And What We Should Be Doing Instead) where I make the case for less worksheets and more Open Middle problems like these.
• I’ve written a book called Open Middle Math: Problems That Unlock Student Thinking, Grades 6-12 that walks you the entire process of using problems like these including:
  • how to choose a problem
  • how to prepare for a lesson
  • how to facilitate classroom conversations
  • what to do when things don’t go as expected
  • how to make your own Open Middle problems

  It’s available now in paper or Amazon Kindle versions.

• I’ve created an online workshop called Empowered Problem Solving that I offer every fall and spring where I dive deep into how to implement these problems (and others like my real world lessons) so that you feel prepared to use them with your students.

 

Some of the problems in this matrix were created by other people and I want to say thanks for their contribution. Those problems include:

• The DOK 2 fractions on a number line problem inspired by Illustrative Mathematics.
• The DOK 2 multiplying decimals problem written by .
• The DOK 3 comparing fractions problem written by Peter Morris.
• The DOK 2 adding multiples problem written by my son, Owen Kaplinsky.
• The DOK 2 multiplying differences problem written by my son, Owen Kaplinsky.
• The DOK 3 multiplying differences problem written by my son, Owen Kaplinsky.
• The DOK 3 multi-digit division problem written by Ellen Metzger.

 

I’m sure that there will need to be tweaks to this matrix, so please let me know if you have any questions, concerns, or suggestions in the comments below.