The most straightforward method I have found for distinguishing between the first three levels of Webb’s Depth of Knowledge (DOK) is to take a single mathematical concept and provide a problem at each DOK level. Here are three examples that illustrate the differences well using:
- fractions on a number line
- perimeter and area
- surface area and volume
I recommend that you spend a couple of minutes trying out each problem before reading the analysis so that you can feel the difference between the problems in terms of stress, critical thinking, and effort.
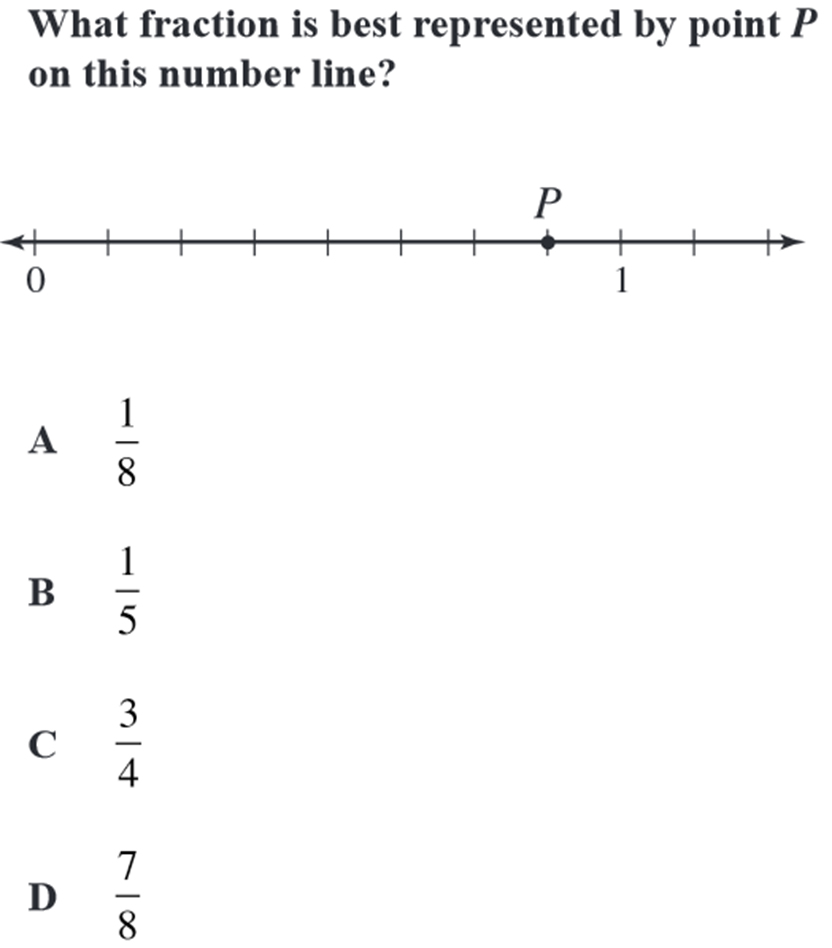
Source: California Standards Test Released Test Questions
DOK 2

Source: Open Middle (inspired by Illustrative Mathematics)
DOK 3

Source: Open Middle
Analysis
Let’s consider the difference between the three problems. The DOK 1 problem is very commonplace. Both zero and one have already been defined so the student needs to notice that the line is divided into eighths and count over seven of them to find seven eighths.
With the DOK 2 problem the previous strategy will no longer work. The one is not defined nor are any fourths. The student has to realize that she can define a one by finding where 3/3 is located and then divide the space between zero and one into fourths. To be clear, this problem is on the exact same topic as the previous problem, but requires deeper knowledge of the topic.
Finally, consider the DOK 3 problem. This is significantly more challenging than either of the others. Two factors that help categorize this problem as a DOK 3 include the strategy and critical thinking needed to find the answer (for example, where do you place the 7 and 9 to make them least problematic) as well as the fact that there are multiple correct answers. There is also significant conceptual understanding built into this problem if you want to minimize the amount of trial and error needed. It is unlikely that anyone solves the DOK 3 on the first attempt while the DOK 1 and DOK 2 problems are much more reasonably solved the first time.
What is the perimeter of a rectangle with that measures 8 units by 4 units?
DOK 2
List the dimensions of a rectangle with a perimeter of 24 units.
Source: Open Middle (via Dan Meyer)
Of all the rectangles with a perimeter of 24 units, which one has the most area?
Source: Open Middle
Analysis
Assuming the students have learned about perimeter of rectangles, the DOK 1 problem is rather trivial. Add up all the sides’ length and you have the perimeter.
The DOK 2 problem is slightly more challenging. As this blog post shows so well, some students have not considered that there may be more than one rectangle that has the same perimeter length.
The DOK 3 problem may not appear to be challenging to an adult, but it can be to students (I have some student work samples to share in my next post). Note that for this problem, you have two basic approaches to solve it:
- Continually guess and check until you find a solution that you are unable to beat.
- Use conceptual understanding of perimeter and area to realize that a square has the largest ratio of area to perimeter for any rectangle.
What is the surface area of a rectangular prism that measures 8 units by 4 units by 3 units?
DOK 2
List the dimensions of a rectangular prism with a surface area of 20 square units.
Source: Open Middle
DOK 3
Of all the rectangular prisms with a surface area of 20 square units, which one has the most volume?
Source: Open Middle
Analysis
If you tried these three problems, I am sure you realized how quickly the challenge increased from DOK 1 to DOK 2 and even further with DOK 3. Assuming students are experienced with using the formula for the surface area of a rectangle, the DOK 1 is trivial.
However even with that knowledge and experience, finding an answer, any answer, to the DOK 2 is not initially obvious. Without the conceptual understanding that the rectangular prism with the largest ratio of volume to surface area is a cube, you will be guessing and checking for days on the DOK 2 and DOK 3 problems.
If you think that this may be an unfair or unrealistic problem, please check out the Smarter Balanced Assessment Consortium’s (SBAC) Practice Test performance task for Grade 6 mathematics. I have included a downloadable version of that problem here. If you look through the performance task, you will notice that the final problem in this task is essentially the same as the DOK 3 problem above. These problems are hard for math teachers, let alone students, to do and they will be assessed by Common Core State Standards’ tests.
Can you think of any other topics that have good examples of DOK 1, 2, and 3 problems? What ways do you use to distinguish between the DOK levels?

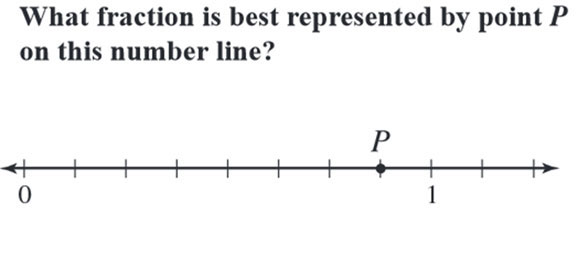
Thank you for this explanation. Depth of Knowledge can be difficult to identify. I recently used the second fraction number line with a group of students. It was incredibly difficult for them. They understood that 3/3 is the same as 1 whole, but they wanted to place it at the end of the number line. For them, this problem was more challenging that the following one that’s a DOK 3. While my understanding of DOK is growing, it’s easy to fall into the trap of thinking that just because a problem is hard, the DOK level isn’t necessarily a 3 or 4.
Agreed. With DOK I think it is certainly a situation of the process being more valuable than the product. Just experimenting with the problems at various DOK levels is better than not using them at all. I am also more concerned with two levels apart than one. For example, if someone thinks that a DOK 1 is a DOK 3 or vice-versa, that is a conversation worth having.