How I Integrate Depth of Knowledge Into Mathematics

I recently shared how I came to realize Webb’s Depth of Knowledge’s (DOK) importance and why I believe that it is critical to integrate these types of problems into our curriculum.  I also expanded into how to distinguish between the DOK levels using specific examples that covered fractions on a number line, perimeter and area, and surface area and volume.  Now I want to build upon those posts by sharing my successes and challenges with implementing these problems and provide resources for doing them with your own students.

I’ll be honest with you, it was a humbling experience that was not pretty and refreshingly reminded me that I have much to learn.  I was fortunate to have the opportunity to teach five periods of math to 7th and 8th graders towards the end of the 2013-2014 school year. I used this time to try out some of the problems I had created but not yet implemented. I came in hoping to get student work samples for this problem:
 

Source: Open Middle

 

If you spend two minutes on that problem, you will realize that it is far from trivial.  It is DOK 3 and is really challenging for adults as well as students.  I gave the problems to students and after they had been working on it for a few minutes, I realized that I had a big problem at hand.  Students’ understanding of subtracting mixed numbers was so low that they couldn’t even complete a DOK 1 problem.  Additionally, their ability to persevere through the struggle was miniscule.  A couple of minutes later I made the call to abandon the problem and try a different one.
 
Next I tried this problem:
 

Source: Open Middle

 

Well this did not go any better. Not only was their order of operations knowledge very rusty but I hadn’t thought it through enough to realize that a calculator was absolutely necessary to solve it. This problem was also abandoned a few minutes later. If you subscribe to a growth mindset and believe in the power of mistakes, then you could say that I was learning quite a bit during this period of time.

I was desperate to find something, anything, that they could be successful with. I had tried two problems that incorporated 4th grade and 5th grade standards, respectively, and had no luck with these 8th graders.  Next I decided to try a 3rd grade standard which was the DOK 3 problem on perimeter and area I mentioned in the previous post.  That problem is:

Of all the rectangles with a perimeter of 24 units, which one has the most area?

Source: Open Middle

 

I will tangent from this story to introduce a worksheet I created (after previous struggles with implementing higher depth of knowledge problems) but had never used.  I hoped it would help students persevere through problem that required deeper thinking. It is called the Open Middle Worksheet (click on the link to check it out).  Three key features of the worksheet are:

• six separate sections for each of six attempts
• points earned for attempt and explanation, not correct answer
• a section for students to reflect on their previous attempt and record how they will adjust their strategy on their next attempt.

 

When I came to class this day, I introduced the worksheet to students and told them, “I am sorry if you get the problem right on the first try because you won’t earn a lot of points. I really hope you make at least a few mistakes so you can get enough points from your attempts.” I wanted to set the expectation that mistakes were a valuable part of the learning process. This is often neglected in mathematics. Consider how in English, no one expects to write a final draft of anything on their first try. The expectation is that there will be an undetermined number of rough drafts and, after many revisions, a final draft. With math, students have the expectation that teachers want a final draft the very first time.

Well, I was right and wrong about students’ ability to solve the problem. I was wrong in assuming that this problem would be easy for them. Students initially did not know how to figure out the answer to the problem. In fact, many of them had trouble drawing any rectangle with a perimeter of 24 units. What I was right about was the growth that the students’ showed in one period and how the many incorrect attempts ultimately led to the right answer.

 

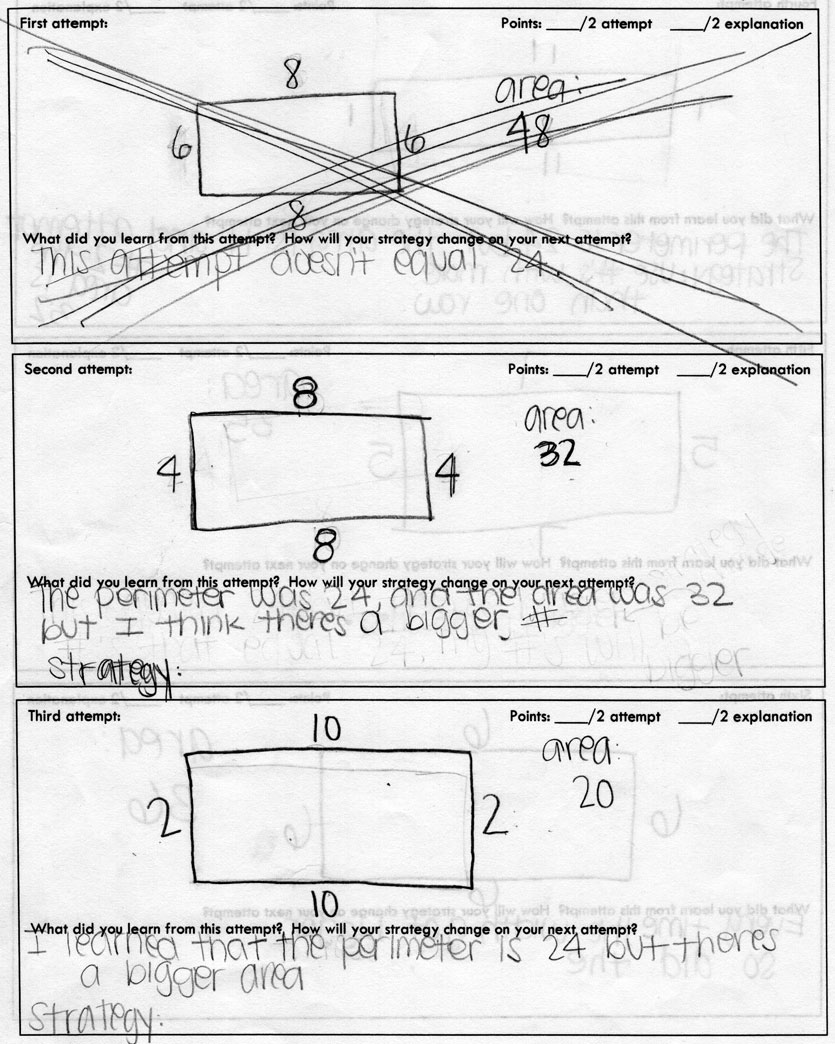
Look at this first work sample below:
 

Front

Back

 

This is one of my favorite student work samples ever.  It starts out so horribly and ends with success.  In the first attempt, the 8th grader couldn’t even draw a rectangle with a perimeter of 24 units! The next attempt achieved a perimeter of 24 units and used guess and check to land in the right ballpark. In attempt three, the student starts using the strategy of increasing the side length to have a larger area. The student notes that this strategy actually resulted in a smaller area. Undeterred, the student tries an even bigger side length and finds the area to be smaller still.

At this point we had a class conversation about what area actually means. Students had little understanding of the square units they were dealing with. We actually drew out the individual square units on a 1 x 11 and 2 x 10 rectangle. They realized the idea that there needed to be more of a balance between the number of columns and rows.

On the student’s next two attempts, it is clearer that this conceptual understanding is kicking in. Finally the student finds the correct answer. To me, this is a really happy moment in teaching. In a series of 5 attempts a student grows from not being able to solve a DOK 1 perimeter problem to solving a DOK 3 perimeter problem. I had students reflect on their growth via their attempts and they were proud of what they accomplished.

 

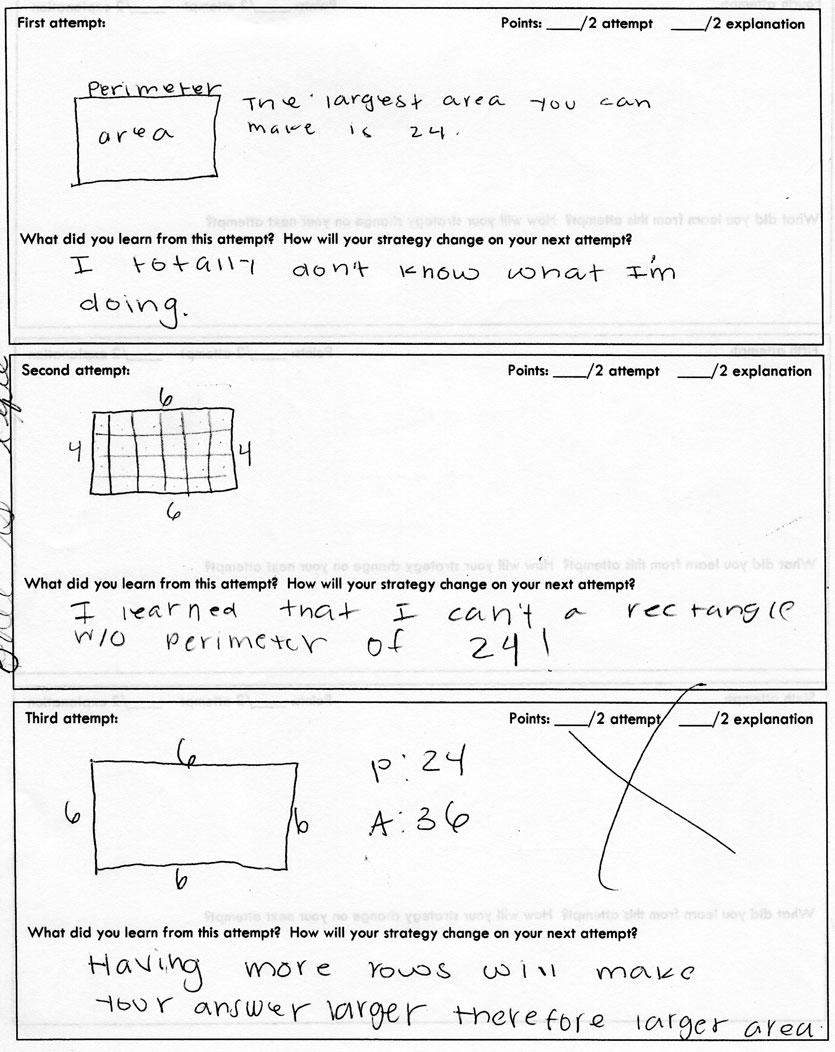
Take a look at these other students’ work:
 

Front

Back

 
Front

 
Front

Back

 
Front

 
Front

Back

 

I believe that there is a place for these problems in math class. I am not saying that they are easy to implement because I continually struggle with getting students to persevere through them. I think that setting the right mindset is critical to success and would love to hear about your own successes and challenges in the comments.

 

Finally, I want to close with a resource you can use and contribute to that has a growing collection of these problems. The website Open Middle, a collaboration between Nanette Johnson, Bryan Anderson, and I, has many DOK 2 and DOK 3 problems at every grade level. We are constantly updating the site with new problems and have a link for you to submit your own problem to add to the collection. The name “Open Middle” was coined by Dan Meyer and is useful to describe the beginning, middle, and end of problems. Open Middle problems are defined by having:

• a “closed beginning” meaning that they all start with the same initial problem.
• a “closed end” meaning that they all end with the same answer.
• an “open middle” meaning that there are multiple ways to approach and ultimately solve the problem.

 

Check out Open Middle, share it with your friends, and please submit new problems that you think are a good fit. By collaborating together, we all grow stronger.