I recently attended a full day workshop with Jo Boaler where she shared a different way of thinking about convincing someone from Thinking Mathematically by J. Mason, L. Burton, and K. Stacey. In the book, she identified three levels of convincing:
- Convince yourself
- Convince a friend
- Convince a skeptic
I immediately realized that this would improve the way I had previously articulated CCSS Math Practice 3:
My favorite way to explain the core of #CCSS Math Practice 3 is “Convince me that you’re right or convince me that I’m wrong.”
— Robert Kaplinsky (@robertkaplinsky) November 12, 2015
That being said, something about it didn’t feel right. Specifically, what does a skeptic mean? Is it someone who has not made a decision and needs to be convinced or is it someone who is actively debating you? Is a skeptic the same as a cynic? I felt like “skeptic” needed to be refined, but I didn’t yet know how, so I started hashing it out with friends and colleagues. Melissa Canham suggested the context of a trial, which has been incredibly useful.
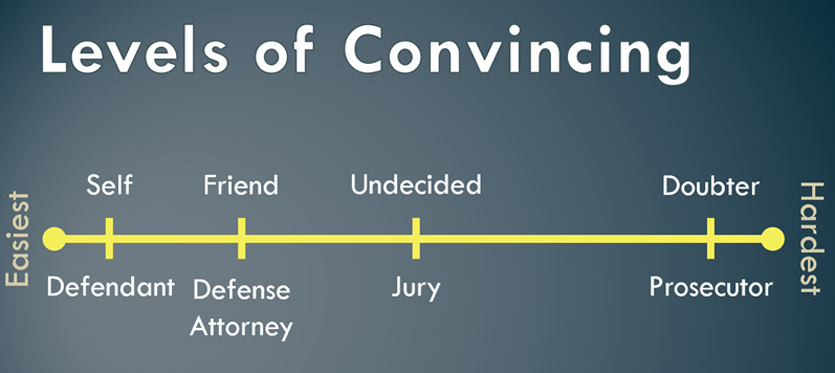
Imagine that you are being sued and are the defendant in a trial. You have to convince others of your innocence, and some will be harder to convince than other. If there was a spectrum that measured how easy or hard it would be to convince others of your innocence, convincing yourself that you are innocent would be the easiest, so it would go far to the left on this spectrum.

The next easiest person to convince would be your defense attorney. It’s her job to get you acquitted and she really wants to believe in your innocence. So, while convincing her will not be as easy as convincing yourself, it still will be relatively easy.

Next comes the jury. Theoretically, the jury presumes innocence and is unbiased. They are looking for evidence so that they can reach a conclusion and want someone to make an evidence-based argument. Therefore, they are neither easy nor hard to convince and go right in the middle.
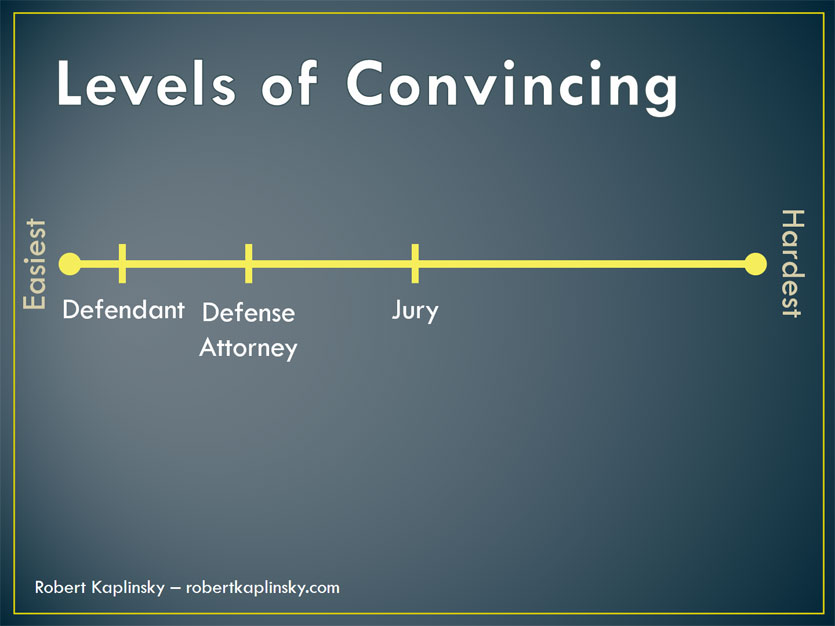
Finally comes the prosecution. They believe that you are guilty and are going to do everything they can to prove it. Not only will they not be easily swayed by what you say, they will actively point out holes in your argument. Accordingly, they go far towards the hardest to convince side of the spectrum.
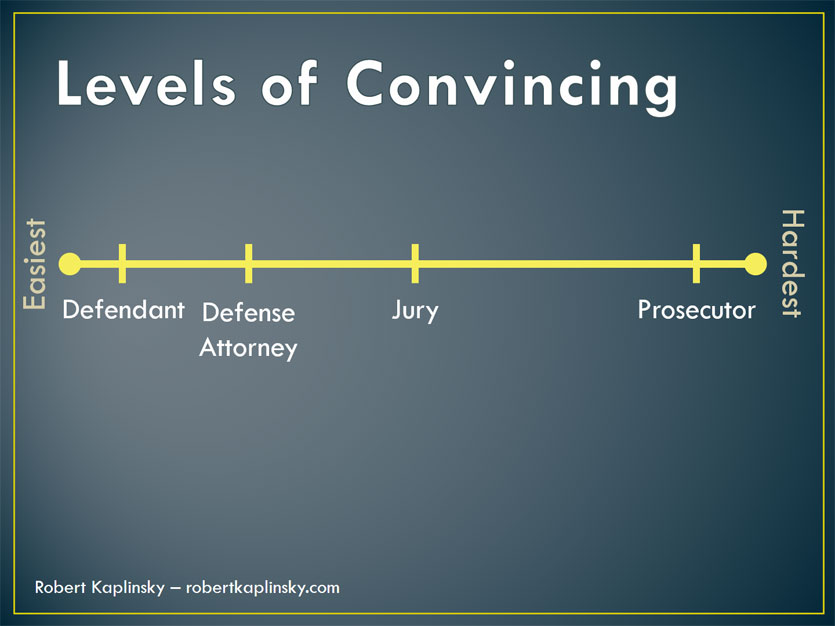
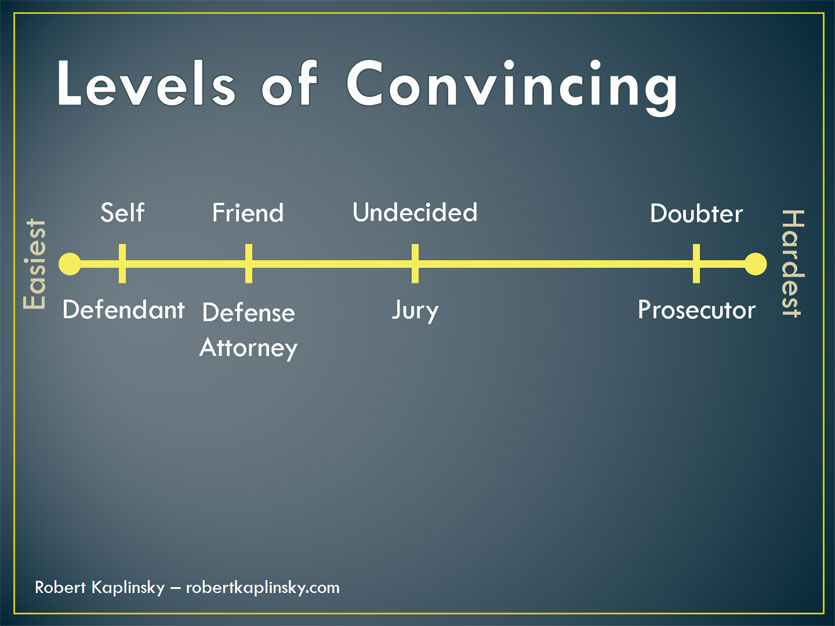
With this context in mind, who then is the skeptic? Is it the jury? Is it the prosecution? Is it both? I don’t feel that the term “skeptic” is precise enough, and so I suggest replacing skeptic with “undecided” and “doubter”. This gives us the grouping below.
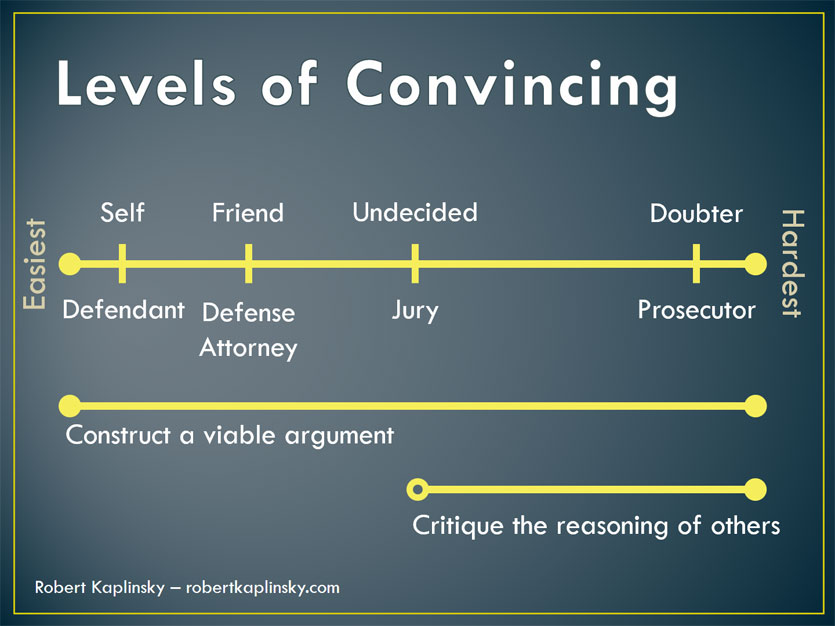
In sharing this idea with Nanette Johnson, she suggested that if you overlay “construct a viable argument” and “critique the reasoning of others” from CCSS Math Practice 3 they would line up as shown in the image below. Note the open circle at “undecided” for “critique the reasoning of others”. Undecided people do not have an argument to critique. However once they’ve settled on a different viable argument, then you will have to critique their reasoning to convince them.
Think about what this metaphor looks like in a classroom context. A student (the defendant) solves a complex problem and then explains her reasoning to the partner (defense attorney) she had been working with. Her partner agrees with her reasoning, and the teacher has the pair of students share their findings with the rest of the class. Some students in the class may have not found a solution to the problem (the jury), and after listening to the students’ reasoning, they are convinced. However, a few other students used a different method to solve the problem and reached a different conclusion (the prosecution). They believe that they are correct and will try their best to emphasize the merits of their methods and critique any others. They may ultimately change their minds, but it won’t be easy.
The jury context may be useful in helping students visualize an audience they have to convince. Too often students equate explaining their reasoning with simply describing the steps they took. Students may not realize that describing their steps is not the same as explaining their reasoning, but they do realize that it wouldn’t convince a doubter, undecided, or possibly even a friend.
What do you think?

I am going to use these visuals to help create a point of reference for my students. This is a great strategy that I can set up in my AVID class, math class and life lesson.
Thanks Daniel. Please share back with how it goes.
I love the visuals…I think the kids will ‘get’ this! I’ll try it soon in my classroom!
Linda Mac
Me too. I am going to include these visuals so that they can delve deeper into their Mathematical thinking!
I like the visuals – however with my k-5 kids I think this would be a little tough to explain.
Brilliant! I bet kids really relate to this. I imagine it crossing over into other areas.
Thanks Anaa. I’d certainly expect it to cross over into other areas as well.
I really like the visuals and it makes a lot of sense to compare it to the court system. I am wondering how we might describe it to younger students that don’t understand the parts of a trial?
Hmm. That’s a good question. I don’t know but if you think of a different context, please share.
Think school setting for little guys. I’d say self, best friend, teacher, principal.
I will be using this over the next week. I’ll let you know what happens with my 2nd-6th grade students! -Rena
Thanks for sharing this. I am going to try using this as a framework for when students are discussing issues in a socratic seminar, so they think about the depth to which they are explaining their point of view and their reasons to support this. It will also enable them to choose from a bank of sentence starters to help guide the way they speak in order to clearly express their thinking.
Excellent. I’d love to read about how it goes.
I find it curious that your courtroom scenario has no judge. Like the jury the judge should begin the process as undecided, perhaps leaning in the defendant’s favor because of the presumption of innocence. The judge is also unique in this situation as the expert arbiter of the law. But a judge still needs to refrain from influencing the jury. The obvious correlation here is to the teacher whose role is to listen carefully to the arguments, orchestrate the classroom procedings, apply rules of law or content knowledge when necessary, and allow the students to come to agreement on the correct solution rather than revealing it to them.
Well Wayne, after reading your comment, I also find it curious. That’s a great addition to the metaphor. The judge is not specifically someone who you convince, but certainly plays a role in facilitating a productive conversation. Thanks for making me think about this!
I am a retired judge. The judge serves as the 13th juror and arbriter of the facts. If the judge agrees with the findings of the jury, the judge accepts the jury’s verdict and enters their verdict and consents to their findings. But if the judge disagrees with the jury’s verdict the judge sets aside the jury’s findings and enters the judge’s verdict not withstanding the jury’s findings (Commonly referred to in legal circles as JNOV – Judgment notwithstanding the verdict, also called judgment non obstante veredicto).
Thanks for this professional insight. I didn’t know that.
Perfect representation of MP3 and matching! It really makes more sense with your visualization.
I do coteach once in a while, but usually coaching. I will share it with my teachers that I am working with. I didn’t share with them yet:)
I believe they will analyze your metaphor!
Thanks Al. Let me know if they have any suggestions for improving it.
I would like to know how you would (use (or have used) this idea and how it could change student responses
Hey Paul. I basically share this same story with them. Then, with that context, I ask them if they think they would have been able to convince a jury or someone who is undecided. It may not be reasonable to convince a doubter, but that is a goal to aim for.
That prompt for them to reflect on their level of convincing is usually helpful.
Thanks for the visual and its explanantion. I could see the parallels in my daughter’s dress shopping. She found one she liked. Her friends were quick to agree. Her mother (undecided) came around, but me, the father (definite skeptic) found holes (figuratively and some literal) in the dress and its perfection. That will be my “putting it in context they understand” example.
This is genius! The dress context is a perfect way to illustrate this idea to students. Students often find themselves trying to convince parents they “need” all kinds of stuff (smart phones, later curfew, etc)
Said like only a father could. Thank you! This context will supplement the court context and help my students.
This is exactly what I needed!!! I had already planned on using a lot more writing and visualizing in math this year. I will also have a cluster of G/T students this year. Having the students explain their thinking, with so many different levels of understanding within the same class, was something I was still pondering. You’ve helped me so much, once again, get the root of what kids need to learn about REASONING.
Great to read Melodi. I’m glad this metaphor has been useful for you.
Thank you for this share. We are trying to improve student communication in our school and school board so this came at a perfect time. I think the metaphor will help students understand the different levels of convincing. I will be translating this to French 🙂
Wonderful Tricia. Maybe you could reply back to this and share a link to your final product so others can download it? Thanks!
I have been using the courtroom metaphor for years as I teach proofs in high school Geometry. I love this visual and can’t wait to discuss with my students. Thank you!
Awesome. Hope it helps.
Like the model which aligns with our communication standards. Wonder how to move non verbal students gracefully to the right?
I guess it depends on what you mean by “non verbal”. Does that mean students who literally don’t have the ability to orally communicate? They could use written language. Does it mean students whose native language is not English and they are learning English as their second language? They might benefit from sentence stems. Does it mean students who are shy or introverted? They might value more individual think time, time to write in a notebook first, or time to talk in small groups.
This is exactly what I was thinking. I have students who are English Learners (new comers) and I was trying to figure out what sentence stems would be helpful to explain their thinking. Today in one of my lessons, I said that not only do they need to explain their steps, but they had to tell me/write why they decided to do that. I gave them these stems “My first step was to _________ because ____________. My second step was to __________ because ___________ .” So, after looking at your visual, I am convinced that this is not enough. However, am I on the right track?
I’m not totally sure Mara. Maybe you could talk with them (your students) and ask what they would like and go from there?
Many TV shows/movies include court scenes so many secondary students would be familiar with it. What I like about this metaphor, is that often it takes a variety of evidence to win an argument in court (at least on TV 🙂 ) Were you able to convince them by using more than 1 strategy? Would a visual help the jury see the connection. Was the language you use concise and easy to understand. Is your solution path convincing and easy to follow? What might a doubter be thinking so that you could prepare to counter their argument? So easy to weave in other math practices. Looking forward to sharing this colleagues!
Great Amy. It’s been my experience that even if kids don’t have a lot of experience with courts, they can still understand this metaphor.
I teach math intervention to littles (1st-3rd grade). I have used a similar metaphor with my kids but using my large family as the example. I have lots of cousins and growing up, we all thought we were Grandma’s favorite… so when we would argue over an issue (“Whose fault is it the lamp broke?”) , Grandma was the jury (mostly impartial), the sibling/cousins who took our side (“the uh-uh’s”) and the opposing cousin(s) (“the nu-uhs”), the skeptic. Pawpaw was the executioner – he would just “whup us all!” Oh. Wait. You didn’t have an executioner! ;0
Ha! I didn’t see that last twist in the story coming. Pretty funny. Thanks for sharing.
First of all, this is lovely. I love the recognition of different levels of convincing, and the visual representation. That said, I have two critiques to offer:
1) Friends can disagree; in fact, it’s very good to have friends who disagree with you and who can show you where you’ve made a mistake. Since I don’t want to promote doubt as a sign of unfriendliness, I want to replace “friend” in your graphic with an antonym of “doubter”, but the first ones I found–chump, dupe, and sucker–don’t sound very good. “Believer” has other connotations that work against us. “Sympathizer” and “accomplice” bump up the grade level more than I’d like, and still don’t hit the bull’s eye. Do you have other ideas?
2) I think it’s important to critique arguments even when we agree with their conclusions. This helps us spot flaws in our thinking and make improvements–or, if the reasoning is sound, may help us recognize places to reuse the argument structure (SMP 8).
These are both great points, Brad. I don’t have alternatives that are much better. I’ll think about it more.
Love this!!!! I’m going to share this with my algebra class tomorrow. We were just reviewing graphing inequalities for domain and range, and the open circle will fit straight into what we were learning for math, as well as provide a springboard for expectations for how we can be better learners. Thank you Robert!!!! I’m a new teacher and soaking up everything like a sponge!
Awesome Katrina. Glad it’s working for you.
I love the metaphor! My students will respond well; and I will also be including the judge on the continuum. Additionally, as I teach high ability math students, I am often faced with the amount of careless errors due to quick mental math. For the last decade, I have them: “Show me evidence of their thinking. If they solved an equation in their mind, then it must be written on the paper….if they imagined an image in their mind, then it must be drawn on the paper.” I find this works well.
Thanks Karen. One thing I’ve been thinking about a lot lately is why we think about groups of students as being “high ability”. Like how did that label come to be and what biases are a part of that. For example, I’ve often found that sometimes we use “high” and “low” to measure how good of a math robot kids are. If we instead changed how we taught, we might find that students perform differently than we expect and that our groupings are more a reflection of how math is taught in the US.
Thank you for raising this point! One of my jobs as a coach is working with the “high” group in a 5th grade class. While these students all excel at calculation and routine tasks, some are uncomfortable—even actively resistant—when I ask them to justify. I asked them why they felt that way, and one of them said that “once you know the rules, that’s all the math.”
Encouraging children to think meaningfully and innovatively requires us to redefine what it means to be good at math (and hopefully eliminate myths of ability in the process).
I am guilty as charged of using terms such as “high ability” and am actively working on changing my mindset around this. Ironically, I am an example of this flaw! When I was in school, I would NEVER win a game of Around the World in math {where 2 students compete on quickly solving a math fact – the student who gives the fact the fastest and/or loudest wins and moves on to the next student}. I knew my math facts cold; but I froze at being on the spot with all of the students and the teacher focused on the 2 of us. I could get out the facts, but was almost always ‘beat’ in being the fastest to move the answer from my brain to my mouth. To this day, I hate that game and refuse to use it. Slower does not equal low ability and faster does not equal higher ability.
It reminds me of this quote from Maya Angelou: “I did then what I knew how to do. Now that I know better, I do better.”
This is an excellent example to get students understanding what we mean when we tell them to “justify” their answers and explain why their solution works. I will work with the Math Team at my school site, and share these visuals to support our students when they are in the process of explaining their final solution and/or justifying their math work.
Great. Glad you find this helpful for your work.
Thank you so much! This is exactly what I needed!
I have a question; What is the meaning of “Students may not realize that describing their steps is not the same as explaining their reasoning, but they do realize that it wouldn’t convince a doubter, undecided, or possibly even a friend”? Can you please explain it more clearly?
Hi Setare. So if I asked a student to explain why the did a step, they might say something like, “First I added, then I subtracted, then I…” or they might say “Well I realized that there were 10 people that needed a ride and that they definitely could not fit in one car so…”
Saying the steps won’t be likely lead to convincing someone about your reasoning while sharing your thought process in context (like with the car rides) might. Hope that helps.
I appreciate your help understanding this.
Hi,
I am a special educator working with third grade. I work in the classrooms and also teach small groups. Getting students to talk to each other about their math and to explain their reasoning has been really tricky.
I want them to see that the math is for THEM, not for me, and I want them to want to figure out solutions because they’re curious as opposed to compliant.
I like this post and can imagine explaining this to high schoolers or maybe even middle schoolers. What about elementary students? Do you have suggestions for language or visuals to help younger students (grades 2-4) wrap their heads around this?
Any advice would be greatly appreciated!!!! Thank you!
Hmm. I am not sure. I wonder if you tried this, whether they’d get it. I remember reading “You Be The Jury” books pretty close to 4th grade.