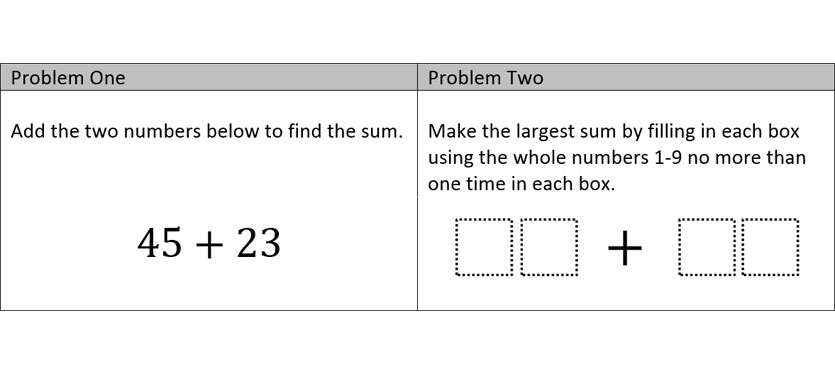
Consider the two problems on adding two-digit numbers shown below that are of varying Depth of Knowledge (DOK) levels:

When I gave both of these problems to my then second-grade son (who is fortunately a mini-math geek like his dad), he quickly conquered Problem One with it providing no real challenge. When I showed him Problem Two, he got 98 + 76. This is a great first answer, but it’s wrong.
He knew which four numbers to use but the problem exposed a hole in his understanding of place value and gave me a great opportunity to ask him questions like, “What does the 9 represent? What does the 8 represent? How does having more tens or ones change the sum?”
I’d make the case that the problem on the left is DOK 1 while the problem on the right is DOK 3 (more info here). Recently though, I got some pushback that forced me to think of a new way to articulate the difference between them.
This person made the case to me that while Problem One may not be rigorous, if a student uses a more advanced strategy, you could have a deep conversation about it. Specifically the person said:
“While a problem such as 45+23 may seem like a DOK 1 problem, if a student explains their solution strategy as ‘I combined the tens and then the ones and added these together as 40 + 20 = 60; 5+3 = 8; 60 + 8 = 68’ [what DOK level would that be?]”
Admittedly, at first I struggled to find a response. I knew that there was a significant difference between them, but I couldn’t articulate it. Then it hit me.
What I realized was that instead of measuring a problem by how deep the thinking could go, what if we measured it by how it avoided the potential for shallow thinking? Take another look at the two problems again, but now think about the least amount of brainpower you would need to solve each one.

Problem One could be solved almost without thinking. You could do this robotically while having a conversation and not miss a beat.
Problem Two is another story. There is no robotic thinking going on here. You could potentially do a significant amount of guess and check, but otherwise you have to strategically think about which numbers you want to use and where you want to put them. There is no realistic way around that.
As such, Problem One has high potential for shallow thinking while Problem Two has low potential for shallow thinking. So, perhaps DOK could be considered a measure of deep, rigorous thinking as much as the avoidance of shallow thinking?
What do you think? What am I right about and what am I missing the mark on?

I agree about the difference of potential of the two questions, but it also raises the importance of what else – beyond the task/question itself – that can elicit deeper levels of thinking and understanding. As you’ve said, DOK is complex, so it’s difficult to reduce to a system of classifying problems. Problem 1 in one classroom may turn out to be a much richer problem than Problem 2 in another classroom, because of the classroom culture and question prompts. But potential-wise, yes, there is a clear difference.
Thanks Marc. Yes, I think everyone agrees with you that great conversations can result from most problems. My realization is primarily your last sentence, that problem 2 clearly has a higher floor in terms of depth of knowledge.
Well, IMO this comes down to something my HS dept has talked about a great deal: the DOK of the response of the student and whether it matches that requested in the problem. The reality is in the second question a student could also just guess, maybe checking the sum or not – either way they may or may not be doIng deep thinking. This is why it is hard sometimes to classify a multiple choice, check all that apply or similar question at a higher DOK because you don’t know if they guessed when in reality it may actually be a more rigorous question. Discourse, the opportunity for feedback, starting an academic fight among students, requiring them to convince someone else, or some other structure is usually required to make sure the student response reaches the level intended in the problem. I agree that certain problems would provide better opportunities for more rigorous thinking, but getting students to persevere and engage in that may take more.
This has been very thought-provoking. Thanks for sharing your thoughts.
I would add that just because a student answered “I combined the tens and then the ones and added these together as 40 + 20 = 60; 5+3 = 8; 60 + 8 = 68” doesn’t mean question one is automatically higher DoK or even the student’s response is. One has to ask “What was that student taught? How was that student taught? How has s/he practiced?” If that class has done tons of problems this way, automatizing this process, then what appears to be deeper thinking is actually DoK 1. The same is true when a class practices taking key phrases in a word problem and building a model and solving the problem. When the student then demonstrates on an assessment that s/he can mimic that process and do the same type of problem following that recipe, then that problem has been reduced to a lower level, arguably a DoK 1.
On the other hand if question one asked the student to find two or three ways to evaluate the expression and compare/contrast those methods, then the student would most likely have to think deeper and express better understanding of numbers — unless s/he was given or practiced scripted answers to those questions. This is could also be achieved by engaging in mathematical thinking and discourse with peers.
This makes me reflect on not only WHAT I teach, but HOW I teach it!
Thanks for your perspective Phillip. It sounds like we are both focusing on different aspects depth of knowledge. Before I get into that, I first want to address a comment you made. You wrote:
“The reality is in the second question a student could also just guess, maybe checking the sum or not – either way they may or may not be doing deep thinking.”
I see it differently than that. With Problem 2, there are at least 3,000 different combinations for this problem if someone was “just guess[ing]”. That would take quite a long time and before long, students would inevitably start thinking about more strategic ways to approach it. With Problem 1, there is one path and you don’t have to think strategically at all.
Your other point is a very interesting distinction that I haven’t spent enough time thinking about: when we talk about depth of knowledge, what are we measuring? Is it the depth of the content knowledge required to solve the problem (what I’ve been assuming) or the depth of the conversation including students’ ability to articulate their strategy (what I believe you are suggesting).
I think both are valuable, but my emphasis has admittedly been on the content knowledge as I believe that most problems could have deep conversations but not all problems emphasize deep content knowledge. Here’s a link to more examples of how I classify them: http://robertkaplinsky.com/tool-to-distinguish-between-depth-of-knowledge-levels/
What do you think? What am I still missing?
In the first scenario, the student would/should have expressed their answer by adding tens first and then the ones. (It doesn’t matter which happens first.) So we have the strategy of using partial sums. If you understand that strategy, the problem is a no brainer. But, if you are learning to choose an appropriate strategy and that is your explanation . . . it becomes a “test” of your skill/strategy knowledge. I understand using strategies to explain the answer to the problem, but it is still only one or two methods and the answer is either correct or it isn’t. If I’m wanting to assess deep thinking, I use something that has multiple entry points and several strategy options and at least one or two solutions.
As an extension… how do you feel about the premise that test items should not be surprises? Theoretically, if students have been exposed to a type of question before and memorized how to “answer” it would that make all non-surprize test questions DOK 1 regardless of the appearance of the question?
I’ll partially agree! I’m not sure I’m willing to say in absolute it makes it automatically DoK 1. However I will totally advocate that it lowers the problem’s original DoK level.
This debate has occurred at a number of my schools in a number of ways. I am pretty firmly of the belief that assessments need to have some question that is a ‘surprise’, some opportunity to see students thinking in response to a novel situation. I have always had some subset of colleagues that pretty strongly disagrees with this claim.
Hi Kasey, Phillip and Jim. I think it is important to bring clarity to what aspect of a problem is familiar. For example, is it not a surprise because students have already practiced problems on this:
– concept?
– DOK level?
– context?
I think it’s also important to bring clarity to what the assessment’s purpose is? Are you formatively trying to determine where students’ skills are at so you can adjust instruction? Are you summatively trying to measure whether students have achieved a specific proficiency level?
Depending on how you answer these question, it will affect how my reply. For example, I could see putting a DOK 2 problem on a formative assessment, even if you’ve never done one before. This might come as a surprise to students as it is difficult, but that information would be useful in determining whether or not to spend more time on a certain lesson. Conversely, I would not recommend putting a DOK 2 problem on a summative assessment if you’ve never used one because it isn’t fair to measure a student’s proficiency on something that was never taught.
So, kind of a long response to a shorter question. What do you think?
This brings up a really interesting question — is DOK determined by the question or the student’s response? It seems that most of the definitions I can find say that DOK has to do with the level of thinking “required” or “necessary” in the task — but then that really makes me wonder, Robert…if you can just guess and check through problem two, does it really “require” more thinking than a potentially memorized procedure in question 1? I suppose the second question requires you to know if you’ve guessed and checked all the combinations of 4 digits, and really…who would check 3024 (I think?) different ways to see if they really had the highest answer. All to say, I think your idea of a comparison of shallowness is interesting. It gets closer to Smith & Steins four levels of tasks (memorization, procedures without connection, procedures with connections, and ‘doing mathematics’), which I am more fond of than DOK. (And it sounds like this is what your original pushback was about.) The first question has the potential to be in any of the first three categories, based on how a student responds (although probably least likely to be simply memorized…I don’t know why you would have this as a known fact, but I suppose you could), but has no possibility of the last — “doing mathematics”. The second question has a higher likelihood of being the latter two, with a small possibility of procedures without connections (as in the case of a systematic guess and check). To me, the possibility of students truly being able to “do mathematics” within a task/question or “procedures with connections” make for tasks/questions most worthy of our time. I haven’t been convinced of a reason for tasks that are ‘procedures without connections,’ and I contend that ‘memorization’ isn’t truly mathematics … its simply a function of your brain, and one we know wears thin with age, disease and disorders.
Thanks for pushing my thinking on this. I think I’ll mull it over some more.
Thanks Audrey. I haven’t heard much about Smith & Stein’s work, but I’ll be sure to look into it more. Regarding problem 2, you and Phillip both mentioned students potentially approaching it as guess and check. I just don’t see that happening. I also got 3,024 (9x8x7x6) possibilities. Before they get to 10th guess, students are certainly going to start thinking for faster or more efficient ways to solve the problem. Therein comes the strategic thinking.
Similarly to what I replied to Phillip, I think that both problems have the potential for great student explanations, but both problems do NOT have the potential for strategic thinking, or as you mentioned “doing mathematics.”
Thanks for pushing my thinking as well. I’ve put Smith & Stein’s work on my read list and will make sure to learn more about it.
Along those lines, I’d ask to what degree is DOK dependent on age/experience of the learner? I have an 8 yr old and a 13 yr old. VERY different audiences, right? What my 13 yr old can do almost without thinking, my 8 yr old really needs to ponder. I think about my students. If I gave the open prompt to my Geometry students, their response would be very different than if I gave it to my AP Calculus BC kiddos.
Hi Jim. Honestly, I am not certain about this. Here’s my best thinking right now…
Anyone doing a DOK 3 problem of the sort we share on Open Middle needs to have a fundamental understanding of the concept. For example, if you don’t know how to add decimals, then this problem is inaccessible (http://www.openmiddle.com/adding-decimals-to-make-them-as-close-to-one-as-possible/).
So, assuming this basic understanding, I’d still argue that this problem is DOK 3 for you 13 year old, geometry student, AP Calc BC student, or adult. Try it out and see what I mean.
I have found that what “experience” means matters too. For example, I have found that experience with the type of strategic thinking used in solving some of these DOK 3 problems is more important than experience in, say, just adding decimals.
That being said, I do get your point and will think about this more.
I really think this also is a natural way to differentiate. If it’s the standard to get students adding and subtracting fluently within 1,000 (3rd grade) then some students will guess and check but they are also getting a lot of practice adding and subtracting numbers (which is really what they need anyway). I think this is okay because it is meeting the students where they are, once they have the practice they can also start to look at the numbers differently and devise a strategic plan to solve the problem. However those students who are more fluent can spend the time starting to think strategically.
So I am seeing a connection/extension here. 45 +23 (as you described adding the tens and the ones) made me decompose the numbers 45 + 23 = (40 + 5) + (20 +3) = (40 + 20) + (5 + 3) = 60 +8.
Structurally, I was able to move from “guess & check” would have done that a year ago to recognizing that the digits 9 & 8 had to be in the tens place (90 + 80) and the (7 + 6) in the ones place and it does not matter if it is 97+86 or 96+87.
I have had the privilege of working directly with Smith & Stein about the cognitive demand of tasks (written & enacted). Terrific and spot on. Many times we overlook the mathematical opportunities in the arithmetic I learned only with algorithms.
Yeah Valerie. It’s not to say that there isn’t deep thinking that can come from 45 + 23, but with the other problem I’ve suggested, you can see that shallow thinking via guess and check would take a long time and would be really hard to confirm that you ever found the greatest sum (unless you guessed almost every possibility).
I find the assessment criterion for “Investigations” used by International Baccalaureate MYP Math to be very effective for assessing Open-Middle style of problems. I use it as a formative assessment of course. The point is that the language in my “Open-Middle rubrics” comes from the IB Investigation criteria. I think it kind of addresses what your talking about. I sometimes scaffold the problems so that there are specific problems tailored to demonstrating each of these levels. Here’s the language in my rubric.
Level 1:
Applies problem-solving techniques to recognize simple patterns.
States predictions based on simple patterns that may not be consistent with findings.
Level 2:
Applies problem-solving techniques to discover simple patterns.
Attempts to describe relationships or general rules consistent with findings.
Level 3:
Applies problem-solving techniques to discover complex patterns.
Adequately describes patterns as relationships or general rules consistent with findings.
Level 4:
Applies problem-solving techniques to discover complex patterns.
Describes patterns as relationships or general rules consistent with findings.
Verifies and justifies these relationships or rules.
Interesting. I’ll have to think about this, because I wonder if all problems lend themselves towards all levels of thinking. I appreciate you sharing it.
Two things come to mind. First, on twitter people were recently talking about complexity and suggesting the notion that its relative to the learner. I think that really applies to these problems. For a student just learning multi digit addition. The problem on the left is complex and discussion worthy. Things progress and the same student now conceptually understands the operation to a reasonable extent and finding activities that embed practice within a larger problem become more important.
The classic example of this for me: is investigating the Farey sequence which forces you to continually do fraction comparisons and operations but in the service of a larger idea.
Secondly, here’s a plug for broadening the definition of open middle beyond create a problem with boxes that requires you to find a combination of digits and solve some constraint. These type problems are fine and useful but there also exist tons of differently structured problems that don’t use these “rules” and lead to different insights. Sometimes the narrower definition seems to be only one people think of anymore.
Thanks for pushing my thinking Benjamin. I appreciate you trying to broaden this. I’m still trying to figure out how complexity works in relation to a learner. Part of me thinks that the learner is not part of the equation and the other part thinks that’s a naive view I will later change.
My understanding about depth of knowledge is that it is the nature of the problem. It has nothing to do with how the knowledge is approached.
Perhaps all you need to add to Problem 2 to invoke DOK are the words, “JUSTIFY that you have created the largest sum…”
It’s not my intention to say that having students justify their thinking is bad. In fact, you can ask students to justify their thinking with either problem. What I am trying to point out is that the mathematics by itself can require different levels of thinking as well.
There are exercises and there are problems. the first one is an example of an exercise. Even though it might be hard for some students to perform this exercise, it provides nothing but to “build” a muscle. The second one is a problem. In this case one is creating a playbook for a game. You can not follow a procedure to solve a problem. You need to understand the structure of mathematics (like; how are numbers formed, magnitude of numbers, what does it mean to add numbers, what does greatest sum mean. how do I get the greatest sum with a given constraints, etc…), and generalize that structure to derive a solution.
Interesting take, Armine. I see what you mean, though I don’t think teachers would universally define exercise and problem as you have. I’m glad that you see the difference though.