I recently surveyed fellow math educators on Twitter and Facebook about whether they would be more interested in hearing about:

  1. how problem-based lessons connects to the Standards for Mathematical Practice
  2. how to incorporate problem-based lessons into a unit

As you can see below, Option 2: on blending problem-based lesson with a unit won by a landslide.

Twitter
Facebook

Prior to this feedback, I was planning on doing option 1 in an upcoming presentation, but I quickly tossed that idea aside.  So, I went about trying to find a way to articulate how I incorporate problem-based learning into a unit and have two ways to show you as well as an additional one to avoid.

Background

Before I jump in to the options, I need to provide some context.  First, I’m going to use an eighth grade standard on volume for my example.  The standard says:

8.G.9 – Know the formulas for the volumes of cones, cylinders, and spheres and use them to solve real-world and mathematical problems.

 

Let’s assume that we are making a unit around this standard and will spend roughly one third of the time covering the volume of cylinders, another third on cones, and another third on spheres.  That would lead to a unit layout that looks something like this image below.

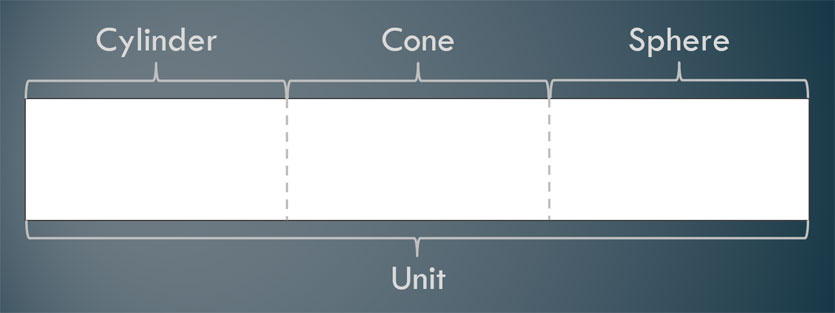
Next, we need to make sure that students have rigorous understandings.  The authors of the Common Core State Standards define rigor as having three aspects:

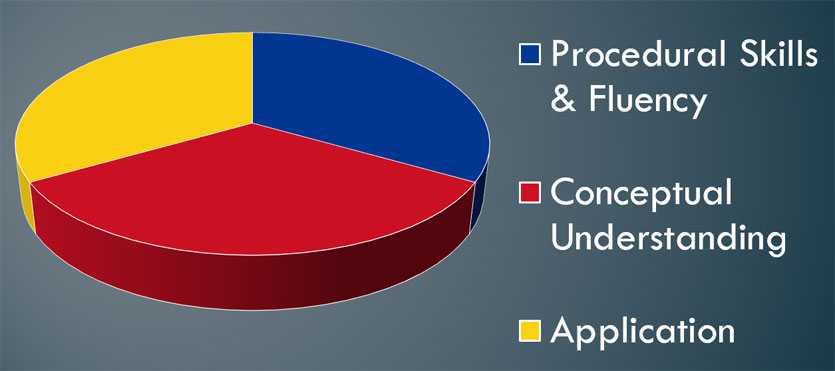
  • procedural skills and fluency (know how to do math operations)
  • conceptual understanding (know why the math operations work)
  • application (know when and where you would use them)

The descriptions in the parenthesis are my crude breakdowns of each part.  Note that to me, application is interchangeable with 3-act tasks, problem-based lessons, and other mathematical modeling problems.

So that we are all on the same page, here are examples of what each of these aspects might look like for the eighth grade volume standard we are using:

The authors specifically mention that “educators will need to pursue, with equal intensity” each of these aspects.  The phrase “equal intensity” does not mean equal days.  Instead it is closer to students having equally strong ability levels.

That leads us to a breakdown like the image below shows.

So, our unit needs to include all three of these components to ensure that students have rigorous understandings.  I wish I could say that this was the way I always taught.  Unfortunately it wasn’t.  When I first started teaching, this image below shows what my units looked like.

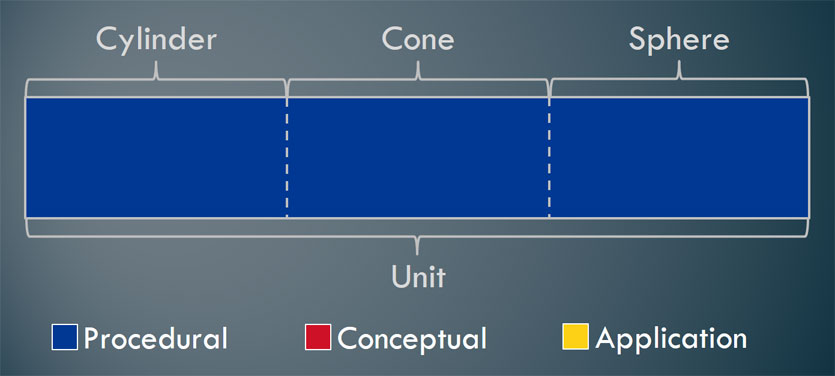
It’s important to put the image above in context.  When I graduated from UCLA with a B.S. in mathematics, I felt like I knew quite a bit about math.  What I came to realize over the years that followed was that, at best, I was a good math robot who could solve problems but really didn’t understand how or why it worked.  For example, I could use a formula to find the volume of a cone, but I had no clue where it came from.  How deep was my understanding really?  And if I didn’t understand that myself, how well could I help a student learn it?

Also, prior to the Common Core State Standards, most state tests focused solely on procedural skills.  As the saying goes, “What’s assessed is what’s taught.”  I spent little time building students’ conceptual understanding or giving them opportunities to apply what they know.  So, when I taught students, I focused almost exclusively on procedural skills and fluency.

Eventually I started integrating conceptual understanding in my units as I learned it myself.  For example, many people know how to divide one fraction by another fraction but far fewer can explain why you change the division sign to multiplication and use the reciprocal of the second fraction.  It takes time to learn why you do that… and you can’t integrate that in if you don’t understand it either.  This slowly led to units that looked more like the image below.

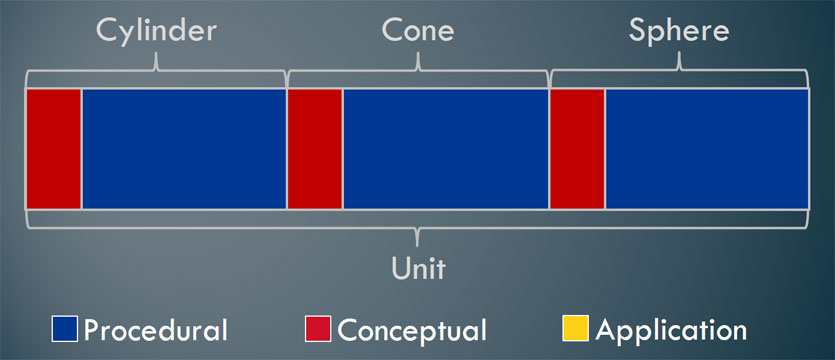
I should note that these images are not drawn to scale.  So, I am not implying that you should be spending 3 or 4 times more energy on procedural skills and fluency.  This will ultimately vary based on students’ abilities.

Now students were getting exposure to procedural skills and conceptual understanding… and this leads us to the main question: how do you integrate problem-based learning?

Option One: Do It At The End Of A Unit

It seems intuitive to do a problem-based lesson at the end of a unit.  After all, one might rationalize that students can’t be expected to apply the math they know to solve a problem if they haven’t learned it yet!  I totally get that point of view, especially as I did this very thing for many years.  That would lead to a unit looking something like this image below (again, not drawn to scale).

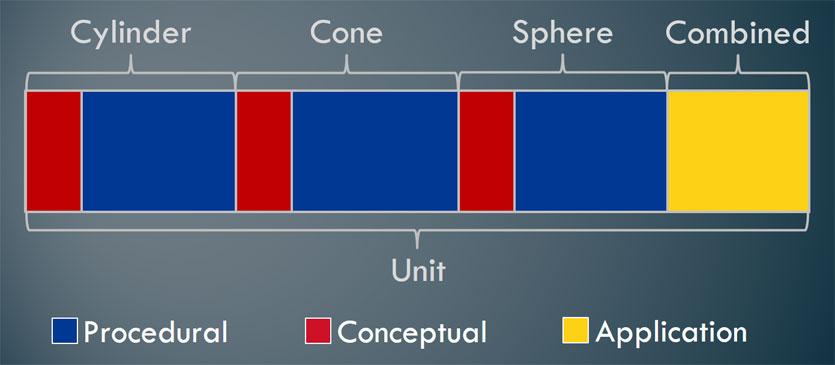
This is certainly better than not doing application problems at all.  However, after all the time that will be spent on the application problem, wouldn’t it be nice to be able to use the context throughout the unit?  That leads us to the next option.

Option Two: Do It Everywhere

Wouldn’t it be great if we could use a problem-based lesson in such a way that students would benefit from it throughout the entire unit?  Fortunately we can, so let’s talk about how to do it.  I’m going to reference my sinkhole problem here, so if you’re not familiar with it, quickly skim it before reading on.

Imagine that on the very first day of a unit, you introduce students to the sinkhole problem.  Clearly they should not be able to solve it.  After all, if they already have the skills to solve it, then why are we teaching this unit?  So, by introducing it to them, they get engaged in a context that the find interesting.  They realize that it is something they want to figure out but currently don’t have the skills to do so.  As Dan Meyer cleverly describes it, introducing the problem here gives students a headache that only mathematics will be able to cure.

So, somewhere in the middle of this first day you get to a stopping point where you have a context you can use throughout the unit and students realize that they want to figure this out but currently cannot.  So, you pause the sinkhole problem and move on to build students conceptual understanding of the first shape.  I picked cylinder but it could have been any of the shapes.

As you build students’ conceptual understanding, you can refer to the sinkhole as a cylinder and talk about what information you would need to know to fill it.  This will lead to building and reinforcing students’ procedural skills as well.  Ultimately, students will have developed enough knowledge about cylindrical volume that you can now revisit the sinkhole problem and try to solve it like the hole’s shape was a cylinder.

The image below (which is not drawn to scale) depicts this process.

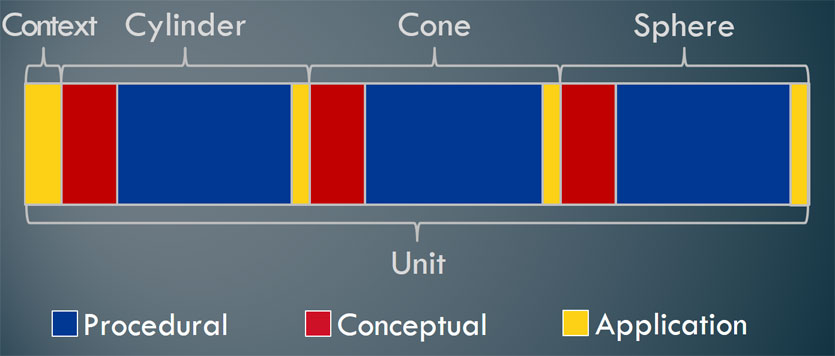
Interestingly, the sinkhole’s shape is not perfectly cylindrical (nor is it a perfect cone or semi-sphere).  So, once students can solve the sinkhole problem using a cylindrical model, next move on to cones and then repeat the process once more with spheres.  Each time through this cycle, students will develop deeper understandings for how to approach the problem.

 

At the end of the unit, depending on remaining time, you have at least three options:

  • as the shape isn’t quite a perfect cylinder, cone, or sphere, you can ask students to combine the mathematical models to make an even more precise model
  • you could give students another problem-based lesson that uses the same standard like this one on a gumball machine
  • you could move on to the next unit

 

Some wonderful outcomes from choosing this option include:

  • You almost never get asked, “When am I ever going to use this?” as students know what they are working towards from the very beginning.
  • A seemingly abstract concept becomes more concrete.
  • The process is a great litmus test. It was something students wanted to figure out, couldn’t figure out, and finally were able to figure out. If they still couldn’t, then you know you’ve still got some work to do.

 

This is my preferred option and I use it whenever possible.  It takes a lot more planning but it is so worth the investment of time.

Option Three: Do It After Standardized Testing

Finally we come to the option to avoid at all costs.  I’d laugh at the idea of doing problem-based lessons only after standardized testing… except that is precisely what I did for many years.  The truth of the matter is that mathematics teachers in the United States have waaaay too much to teach in a single year and it’s easy to feel overwhelmed.

This forces teachers to make tough choices, and a sacred cow that is frequently slaughtered is the problem-based lesson.  Teachers might say, “I know it’s important but I just don’t have time now.  I’ll fit it in at the end of the year after standardized testing when I have more flexibility.”  Again, I get this because I’ve been there.

With more perspective now, I realize that this is not a good choice.  Yes, there is not enough time, but this is not the thing to cut. In fact, doing these problems as I suggest in Option Two may wind up saving you time as students will have deeper understandings and require less remediation.

Conclusion

While doing problem-based lessons somewhere (or even anywhere!) is better than not doing it at all, some options are certainly better than others.  Have conversations with your colleagues about how you can make time for these lessons so that students develop more rigorous understandings.

Please let me know what you think in the comments.  Did I miss another option that you use?  What is unrealistic about what I’m saying?  I look forward to learning from you.

32 Comments

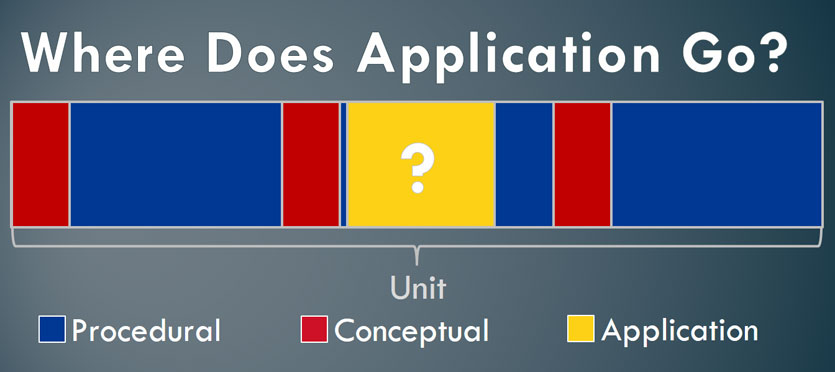
  1. Thanks for this visualization, Robert!
    Many teachers I talk to ask how lessons geared around “application” or “conceptual” narrow into “procedural” by the end of the period. This small scope often leads to quickly funnelling toward the procedural and doesn’t honour the other two categories.
    Widening the scope allows us to treat the unit as the coherent component of analysis. Some days will focus entirely on one of the three, but key is providing opportunities for all of them by unit’s end.
    You used the metaphor of diet; don’t eat everything at every meal, but should get all requirements over time.
    I like the idea to start, but then got wondering, what would I binge on to wreck my diet? What is my math education dessert? Maybe this is the attitude that causes undue tension in mathematics circles. Some see “application” and “conceptual” as a dessert of sorts–not necessary, but a nice treat. This is a refreshing post because it assumes that all three are key to a healthy mathematics diet.

    Reply

    • Thanks Nat. Great points. Your second to last line really resonates with me: “Some see ‘application’ and ‘conceptual’ as a dessert of sorts–not necessary, but a nice treat.” I agree that this is the view of some, because that is exactly how I used to view it (“Let’s teach them how to do the mathematics and if we have time we can teach them why it works or where they would ever use it.”).

      With more perspective, I see that this view was short sighted.

      Reply

  3. Unit structure is so important. Thank you for such a thoughtful post on it! We’re trying to define what math might/should look like on a typical day and Andrew Stadel’s Ignite at NCTM Annual has been helpful. But, maybe we need to back up even further and examine what a unit should look like – then we can better define how our time might look during a week and then a day.

    You wrote “However, after all the time that will be spent on the application problem, wouldn’t it be nice to be able to use the context throughout the unit? That leads us to the next option.” This seems true to me – being able to refer back to that context throughout the unit would be powerful. I also like the idea of starting with a rich task because within the task, the focus concepts become apparent – starting with a rich task lends itself to developing and defining concepts.

    Reply

    • Thanks Chris. It sounds like you had many of the same thoughts that were bouncing around in my head too. Yes, using that context over and over again is really helpful.

      Reply
  4. Pingback: Two Ways To Integrate Problem-Based Learning In...

  6. I was felt identified with you. In the past, I solely taught procedural skills. Now I have taught these plus conceptual. And “tomorrow” I will want to teach application skills. My plan is to follow your advice here with my upcomming next course (february). The idea is a “little step further”: no units. Just problems and theory we need to solve (in many ways) the problems. So if algebra and proportionality reasoning are used to solve problem A, then “explain” those.

    A big thanks,

    Reply

  7. Love the visual for the 3 aspects of rigor. I, too, struggled for years on how and when to incorporate application/pbl into my lesson plans. My question is in regards to assessment. Do you consider the application piece (3-act task, for example) to be the assessment of the unit or not?

    Reply

    • Sorry I missed your question for so long, Caroline. No, I don’t consider the application piece to be the assessment. It’s just another component… and perhaps the most important… like it’s great to know why something works and be efficient at doing it, but we need to give kids practice actually applying it.

      You might include application in the assessment, but it’s not something you just put in the assessment. It’d be like having a driving test to get your license without ever letting kids practice driving.

      Reply

  8. I know I’m going off on a little tangent, but I think a couple of years ago was the first time I learned and understood the relationship between the volume of a cylinder, cone and sphere. When I used the traditional formula for the volume of a sphere, 4/3(pi)r^3, I could never remember it because it didn’t connect to anything, it was just another thing to memorize.
    But then I: 1) Started using the equation V=Bh (okay, many years ago), and 2) Saw the videos that related a sphere with a cylinder and a cone with a cylinder. I thought about a tennis ball in a container, and could imagine the space being the remaining â…“ of the volume. So now I think of the volumes as cylinder: Bh, cone: â…“ Bh, and sphere: â…” Bh, with h=d=2r. Everything fits together and it makes so much sense! And it’s easy to see how to go from V= â…” Bh to V=4/3(pi)r^3, so students can choose which equation they want to use. (But I really want them to see why 2/3Bh is something they won’t forget – and it seems like they forget the cubed in the traditional equation, and revert back to pi(r)squared because that’s what they’re used to with finding area.)
    Thanks for your blog and letting me take this tangent as a comment!

    Reply

  9. Wow Robert,

    I’m only beginning this journey, and love this to bits, but am somewhat still confused as to how all these things can fit in a unit. I’m in Australia and like you it’s always packed with content. Each day our unit would include a new skill. And each unit feels like it has 12 or so skills, taking up all of 3 weeks. Our school is also low socio-economic in background so kids already struggle.

    I am going to give this a go, and am hoping that the “sinkhole” at the start will drive their desire for knowledge and give them a desire to learn the concepts quickly.

    They will find it hard to wait for the solution. They’ll want it that day. I guess this is the bait to string them along…

    Do your let the kids tackle the problem based task generally within one lesson once they’re ready, or do they span across several lessons, one puzzle piece at a time?

    Thanks,
    Really loved this one.
    xx

    Reply

    • Thanks Renee. Lots of great questions and reflections… and lots of it depends as answers. Here are some thoughts:
      – I have seen teachers go through topics and save time at the end to review before a test. I wonder if instead of using that time to review, if the time had been spent at the beginning by building in the context and desire from a problem-based lesson, if it would have minimized the need for reviewing and either didn’t add much time or even reduced the overall time needed because of less intervention time.

      – While in the image, I made it look like you come back to the lesson at the end of the unit, truthfully you can come back to it whenever. For example, sometime before the end of the unit, students may realize that they have the skills they needed earlier. At that point, you can go back to the problem-based lesson. It’s up to you.

      – As to letting them tackle the problem in one lesson or across several lessons, again, this is a “it depends”. For example, the sinkhole problem really lends itself to multiple approaches and merits coming back to. Other lessons, like my In-N-Out burger problem don’t really need so much coming back to and can often get completed in a period or two.

      Hope that helps!

      Reply

  10. I will have to share this sinkhole problem with our geometry teacher, she will love it! I think this blog is perfect timing as I begin to think about planning my spring semester. It’s easy this late in the semester to get tired and fall into the rut of procedural-procedural-procedural. This was just a nice reminder. I always do this really well towards the beginning of each semester but towards the end I slip a bit. Thanks!

    Reply

  11. This was so helpful in how to integrate these problems into a unit. I really liked the “flow” options in regards to the 8th grade standards on volume. It all links together so logically! I would love hearing how teachers have used this same line of thought in planning out other units of study to seamlessly integrate these problem-based lessons.

    Reply

  12. We will be revising our scope and sequences soon. I was already planning to make the three pillars of rigor an explicit part of our scope and sequence. Thanks for posting this as it speaks to exactly what was rolling around in my mind. I think it just became mandatory reading before beginning our work 🙂 Thanks again.

    Reply

  13. “For example, many people know how to divide one fraction by another fraction but far fewer can explain why you change the division sign to multiplication and use the reciprocal of the second fraction. ”

    We were having this exact conversation the other day at a math pd. Now, where’s the link to your blog post about the conceptual understanding of this concept?!? LOL.

    Reply

    • Hahaha. Believe me Rebecca, I need to be *attending* the PD for building conceptual understanding. There are many things I know how to do without actually understanding.

      Reply

  14. I love so much about this, Robert. My only wish is that the diagrams were drawn more to what you feel should be scale. I fear that educator who miss your “not drawn to scale” notes will visually look at the images and assume that procedural work should be done more than the other two. Personally, I would prefer to see that be the smallest portion of the visual image.

    Reply

    • Your point is heard, Erika. I’ve definitely gotten that feedback before. I think that part of what makes this challenging is that the variability in all of this. Like I could potentially make a diagram for this standard, but even then it would depend on everything from what knowledge students have coming in to the how comfortable students were with what they learned.

      I certainly hope people see this as a conversation starter regarding the need to incorporate all three components and not some sort of definitive guide to how much time to spend on each method.

      Reply

  15. I love this and would love to share with my elementary teachers (3-5). Would you have an example for these grade levels?

    Reply

  16. Lovely post, Robert. Your paragraph on graduating with a degree but only aware of calculational orientation for problem solving perfectly illustrates how we grew up learning mathematics in the US. I like your exemplified shift to conceptual orientation and the ways you can embed “making sense of the math” throughout a lesson, not just after after procedural or conceptual understanding has taken place. We definitely do not all learn the same, but foundations for reasoning is something we need to foster.

    Reply

Leave a Reply

Your email address will not be published. Required fields are marked *

Post comment