Several years ago I had a profound moment that led me to completely rethink what it meant to understand mathematics. I was still in the classroom and had been working with 6th graders on adding and subtracting mixed numbers. My formative assessments and observations showed that most students were proficient, and I felt pleased.
To end the unit I gave students an application of subtracting fractions using the context of a freeway sign with fractional distances. Specifically I gave students the picture below (which is the first picture in this lesson) and asked them “How far apart are the exits for Junction 90 and Jefferson Blvd?”

I clearly expected students to do well with this problem, but as I walked around checking students’ progress I realized that something strange was going on. I saw answers like:
- 1/3
- 1 1/3
- 3 3/4
Relatively few students got 1/4. When I asked a student why she got 1 1/3, she said, “It is 1 1/3 because 1 1/3 is between 1 1/2 and 1 1/4.” I felt like it must have been April Fool’s day with the joke on me. I didn’t know what had happened. Was I wrong thinking that students were proficient… or worse… could this minor little context have thrown students off so significantly?
I needed to know for sure, so the next day I came to class and asked students what I considered to be the same problem with no context at all. I just wrote 1 1/2 – 1 1/4 on the board and asked them for the answer. Again, the results shocked me. The vast majority of my students got the correct answer of 1/4. I didn’t know how to reconcile the results of the two problems and this is when I started asking myself “What does it mean to understand mathematics?”
In the days that followed I reflected upon what happened and I decided that my students primarily had procedural skill and fluency but very limited conceptual understanding or the ability to apply mathematics. I realized that for my students to “understand mathematics” they would have to have a more balanced understanding that included all three. This experience provided the foundation for why I value using real-world applications whenever possible. They provide a context for building the conceptual understanding and procedural skill needed for rigorous mathematical understandings.
Now out of the classroom, I work alongside teachers and my goal is to help them realize why the Common Core State Standards state that “educators will need to pursue, with equal intensity, three aspects of rigor in the major work of each grade: conceptual understanding, procedural skill and fluency, and applications.”
To accomplish this I recently recorded myself working one-on-one with sixth graders completing the same problem that had been so meaningful to my professional growth. I wasn’t sure if I could duplicate the results I had experienced years earlier but my plan was to begin each interview by asking the student about the freeway sign and then, regardless of how he or she answered, ask him or her to do 1 1/2 – 1 1/4.
Watch the first video below and note that I sped up time when he was working to make the video shorter.
Is this student demonstrating a rigorous mathematical understanding? Does he have:
- Procedural skill and fluency
- Conceptual understanding
- The ability to apply mathematics
To me it appeared that he had none of these mathematical understandings. Now watch the follow up question with the same student. Again I sped up time when he was working to make the video shorter.
Like I experienced in my classroom, to my surprise he got it right and it appears that this student does have procedural skill but could not navigate around a minor context to actually apply what he knows. He has limited conceptual understanding to fall back on. Clearly this one student is not representative of all students; however it has been my experience that students with superficial mathematical understandings exist in most classes.
Here is another student’s experience with the two problems. Note that I did not speed up the video so you could see the time he spent thinking.
How do you reconcile what you just saw? On the one hand you have a student who found the freeway problem so challenging that he sat for over thirty seconds thinking about how to solve the problem before giving up and stating, “Dang. This is hard.” Then he proceeded to solve the same problem procedurally and explained his process in a reasonably thorough manner. If you had only seen him solve the fraction problem, would you think he could solve the freeway problem? Does he have the rigorous mathematical understanding required by the Common Core State Standards?
Something also worth considering is how subtracting mixed numbers has been and will be assessed. The problem below is from the California Standards Test released test questions. Would these two students get this problem correct? Will this question determine whether they have a rigorous mathematical understanding?
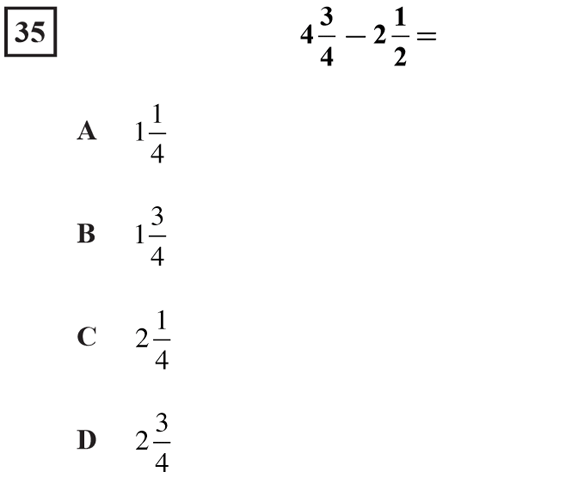
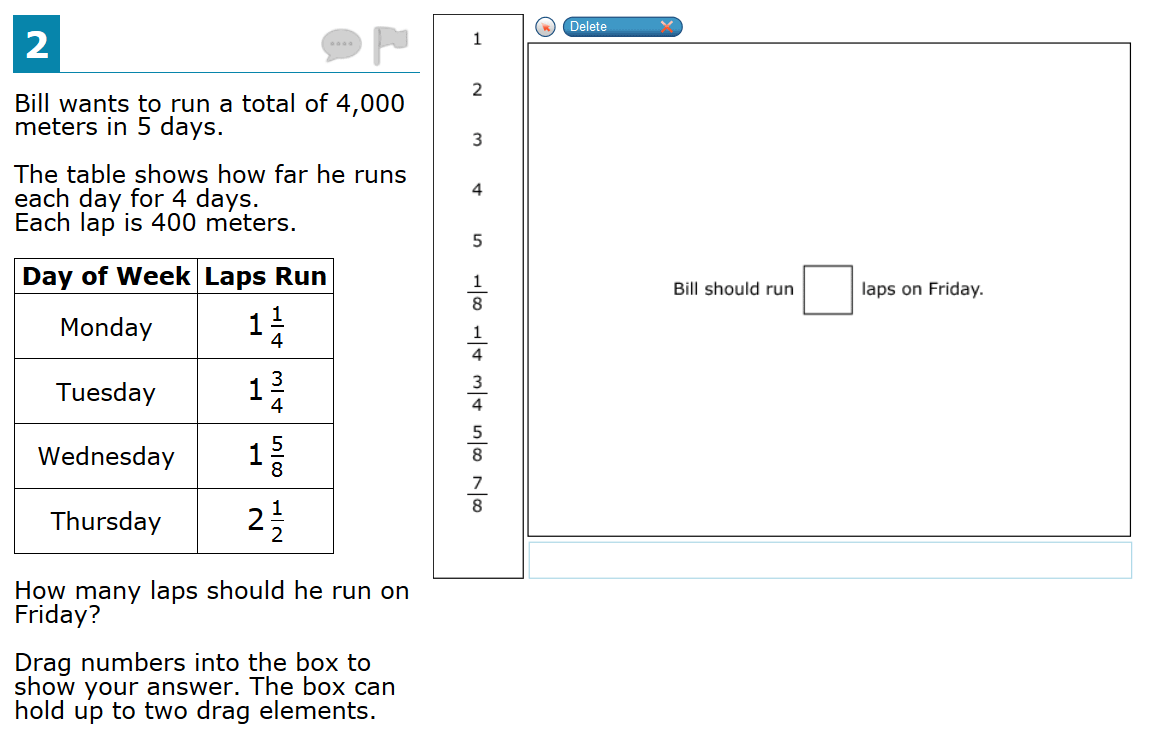
This problem is from the new Smarter Balanced Practice Test for Grade 5 (Question #2). Would these two students get this problem correct? Will this question determine whether they have a rigorous mathematical understanding?
It is critical that we give students opportunities to develop rigorous mathematical understandings. Procedural skill is still an essential piece but it is just as important as developing their conceptual understanding and the ability to apply mathematics. Often times we teach students how to do mathematics with the belief that they will be able to apply it when the moment comes. Clearly that is not always the case.
Let’s get people talking about this. The more math educators are aware of this issue, the better equipped they will be at addressing it. To help in this cause, I am providing the student videos for you to download and use with your colleagues.


Wow. You definitely showed here that procedural fluency has little, if any, transfer over to the real context of “how far apart are the junctions.” You’re right, we want to believe that kids will apply what they learn in chapter 4 section 5 to a real-life situation when they see it, but the reality is learning skills in isolation may very well result in vacant lots of thinking.
Thank you for sharing this important reminder, Robert.
Thank you Fawn. It was my hope to show that procedural knowledge doesn’t always transfer over to application.
I completely appreciate this post. This is a really good example of procedural versus applied mathematics. I especially like you closing argument about “giving students opportunities to develop rigorous mathematical understandings.”
If I may, let’s consider the context of the highway question and the Smarter Balance question. I only mention this because my students recently reminded me on my end-of-the-year survey to use more applicable contexts. One girl said, “I really don’t care how many cups it takes to stack to your height.” Fair enough.
That said, will a fifth grader (possibly English Learner) really be interested in the distance between freeway exits? Does that mean anything to them? They don’t drive nor are they even close to the driving age. Would a fifth grader be tasked with knowing the distance while driving in the car with an adult? They’ll most likely perceive that as the adult’s job. Not all kids have Christopher Danielson as their dad, right? I think the highway question is a great question for high school students. Same with the Smarter Balance question, why would a fifth grader really care about Bill running and the amount of laps? I bet most fifth graders don’t have exercise plans or personal trainers. I’m being honest here because I was that kid. I still am. I would be the kid who says, “Who cares about Bill and his laps? He should figure it out.”
I’m not trying to take anything away from your work here. Trust me, this conversation needs to happen between math teachers and departments. I love that you posted this. I’m curious how the students would respond to something they could better connect fractions with. I’m not entirely sure what that might be, but maybe something in History like:
5.2.3. Performance Standard:
Trace the routes of the major land explorers of the United States, the distances traveled by explorers, and the Atlantic trade routes that linked Africa, the West Indies, the British colonies, and Europe.
You’ve raised a really important challenge to teachers. Thanks for doing this. After this year, I realize I went a little too far away from procedural understanding and really focused on applied and conceptual. Thanks for reminding me to work toward that happy medium of all three.
The work is amazing Robert.
Andrew’s point is one I constantly struggle with – when we design tasks do we think about the students’ perspective? For instance, I see so many textbooks with contextual examples about golf when teaching negative numbers. Who cares about being under par?
With that in mind, we need to look at research and talk to our students about their interests when designing tasks – not to mention engage them in the design.
Eric,
I totally agree with you about negative numbers and real world applications. In addition to golf being unrelatable, we have no negative temperatures in Southern California and no negative elevations either. I have actually found one reasonable context for negative numbers that I plan to turn into a lesson when I have time, but even that is a stretch.
You could use other parts of California that should be familiar to the SoCal kid, HAHA. FYI: Negative temps may occur in the mountains of California (Yosemite, Mammoth, and Lake Tahoe are not that far from SoCal), land height under the sea could be thought of as negative, Death Valley is below sea level, how far under the surface of water is the surfer/shark, …
I suppose everything has a context. My question is do we teach kids about context or do we always have to grab something already in their contextual view (as many have suggested in the thread)? It seems context comes from reading comprehension and maybe that is the real issue and not the math at all? Once upon a time when I was just like a millennial, (35 years ago), the studies at the time pointed out that the correlation between math success and reading comprehension was a holy grail of instruction. To me the kids don’t understand context because they don’t know how to read (signs, billboards, text, etc.). I think asking the questions about what the sign means before even presenting a math problem is certainly a key point others have already said in this thread (ie: teach context first or at least give them a chance to discover the context).
This is a bit complex to respond to. In real life, when you are unfamiliar with a context, you ask questions. I got solar panels on my home. I didn’t know anything about solar panels so I asked MANY questions. The problems happen when people are unfamiliar with the context and cannot ask questions or don’t realize the can ask question (or feel comfortable doing so).
Could you share the context for negative numbers you are referencing here?
Thank you!
I tend to introduce negative numbers with my younger students as money you owe someone. You go to the mall (if they still do) and you want to buy which costs $45 but you only have $10. You convince your friend to lend you $35. Now you have and you owe them $35. That’s a balance of -$35. Seems to make sense mathematically to my young mathematicians.
My first year teaching, I referenced a silo filled with grain and the urban high school students had no idea of what a silo was. Being aware of culturally biased concepts is something to consider as well.
Andrew and Eric,
Your points are very valid, and like Eric said, “one I constantly struggle with.” The Common Core State Standards frequently mention “real world” applications but what is the real world anyway? For example, I have a few lessons that involve store discounts and choosing the best coupon that are very real world. However, markups and discounts are a 7th grade standard and at that age, figuring out which coupon is the best is not part of their real world.
I strive to create lessons that are as close to what students at that grade level actually experience. Clearly that won’t always be the case and the only choice I see is to build students’ background knowledge to include other contexts as well.
Thank you both for your thoughtful comments.
I’m constantly challenged with this too. The fact that we recognize this challenge and continue working toward resolution is key. I agree that some applications aren’t “real-world” for students and you couldn’t have said it better:
“I strive to create lessons that are as close to what students at that grade level actually experience. Clearly that won’t always be the case and the only choice I see is to build students’ background knowledge to include other contexts as well.”
Building that background knowledge has really given me mileage in the classroom with students. Keep up the great work!
I am a little late to this thread, but I understand the dilemma between ‘real-world’ and making it meaningful to 11 year-old students. I try to make word problems that are relatable (making goodie bags for a party, floor plans for their dream room, etc.).
However, I also find it valuable to keep the golf problem as well. I didn’t grow up in a “sports” family and I knew nothing about golf until taking it for a gym class in college! I am still not a fan of the game. However, learning about topics, such as sports, provides students with some background knowledge that they might not learn about from home. I have found that when I ask “does anyone play golf?”, I sometimes have students who are avid players and share their love of the game. It can help make connections with and between students that are unexpected.
I wondered the exact same thing about the context of this problem for 5th graders, but I do think that it can easily be connected to things they have experienced with a brief intro of instances that they have traveled somewhere with their parents. Although the students may not be applying math to this particular situation yet, it may just change what they notice or think about the next time they are traveling with their parents, and it is most certainly an applicable life skill that they will use someday.
Great post. Can’t wait to share it with my teachers. I am always talking to them about the need to go beyond procedural knowledge and to teach students how to think!
Thank you for sharing this work. It’s so easy to get caught up in teaching the “how” and forgetting to let students figure out the “when” and “why.” What really made me cringe is that the first student doesn’t seem to have second thoughts about his answer…he’s not making any meaning of the context OR the numbers.
All good points Kate. I also think of the three parts of Rigor like you describe:
– Procedural skill and fluency is the “how” math works
– Conceptual understanding is the “why” math works
– Application is the “where” math is used.
Yes, the first student does a great job of showing what the Standards for Mathematical Practice DON’T look like, especially MP1.
Wow! This really opened my eyes… What seems like an obvious application of the skill shown is clearly not at all obvious to students. Thanks for making me think…
Thanks Mary. When I created this problem, I also thought it was an “obvious application.” Then I wondered how obvious it was. Clearly, as people who have seen this video point out to me, this student is not a driver and may not have had to think about the sign. However I have also given this problem to a 2nd grader who still sits in the back seat of the car and she got it correct with no help.
Definitely something worth reflecting on.
Good to know that a second grader understood it.
That is very interesting to watch. Thank you for posting.
I like the highway problem, but think the context is actually quite challenging. Thinking in terms of how much distance is left to go is much harder than thinking about how much distance has been covered – I see this struggle every year with algebra I students. In this problem you have to think about two “how much left to go” distances. I would not be at all surprised if many students struggled with this given whole numbers.
The Smarter Balanced problem is easier in some ways. In the highway sign problem the mind is thinking about how far you have already driven & the total length of the trip even though that is neither relevant nor available information. In the Smarter Balanced problem I have the whole story. The total amount is going to be 10 laps. So far I have run such and such laps. It is not a procedural question, but much less abstract than the highway question.
Finally, the first student does not seem to have the procedural side completely nailed down. Looked like he did 5/4 x 6/4 = 30/4 = 7.5.
l hodge. Funny that you should say “I would not be at all surprised if many students struggled with this given whole numbers.” I didn’t mention this in my post but the next day, in addition to asking students to do 1 1/2 – 1 1/4, I also gave them the same freeway problem but changed the distances from 1 1/4 and 1 1/2 to 3 and 5. To my even bigger surprise, some students told me that the exits were 8 miles apart! So, you are very right that the context is a challenge… and one we should expose them to.
I also agree that the SBAC problem is easier. I wasn’t able to find any other subtracting mixed number problem from them or on Illustrative Mathematics so this was the best I could do. My main goal was to show the increased rigor between the outgoing California Standards Test and the incoming CCSS assessment.
Another good point about the first student’s procedural knowledge. In my mind, the main issue was that he did not know what operation to use with the two fractions. He correctly converted them to improper fractions, did multiplication, and then got that procedure wrong. He did well with subtraction though.
Thanks!
Great post. I wonder though whether the problem might be whether your students understood what the numbers on the highway signs mean. (They are, after all, 6th graders and probably never drove!)
It looked like the students understood that you had to do something with the fractions 1+1/4 and 1+1/2, because they were on the lines you had pointed to, but because they didn’t understand what those fractions actually stood for, they didn’t know what that something was.
The street sign itself is not a physical analog to the problem. Without understanding what the street signs mean, you won’t be able to derive the right mental image. Had you helped by shown them a variation of the below diagram, would they have understood the problem better?
Current Location JCT 90
Current Location Jefferson Blv
Would they be able to solve the problem then?
Lisa, you bring up a really good point. If I could do these videos again, I would have begun by asking the student to explain what they knew about the picture of the freeway sign. That would have helped isolate lack of understanding the context as the problem.
I think that’s a great approach, Robert?
“What do you notice?”
“What do you wonder?”
Fantastic demonstration of difference of procedural and real world. But , the understanding of context (as Lisa first put it) was my first thought also.
I certainly did not know (or care) about distances to junction exits at that age. though I was strong in maths. Could students your graphically display the info (even to scale) using a line with 3 points. ? If they can do that they can solve the problem. Without it i don’t think maths knowledge is the problem per se.
Vikas, (Training to be a maths teacher, UK)
Oh my! This post needs to be shared with every math teacher in every school everywhere!! 🙂 Along with the thoughtful comments.
I will be teaching 6th grade math for the 1st time next year and am so nervous about doing a good job with them.
Thanks for this post which was definitely an eye opener!
Shannon
http://www.irunreadteach.wordpress.com
Hi Shannon. Thanks for the kind words. Good luck with 6th grade next year and let me know if you need help finding resources.
Hi Vikas,
Thank you for your feedback. Clearly it would have been helpful to first ask the students if they understood the context. Your point about what being able to graphically display the info is valid, but part of the issue is being able to decontextualize the application to know that creating an abstract, linear representation is a strategy that may help.
Also, your point about what students are interested in and aware of is very valid. As Eric Milou and Andrew Stadel pointed out, finding the balance between real world context and grade level standards is an endless challenge.
Thank you and good luck with your training. Your ability to reflect and analyze situations will serve you well.
Hi Robert,
May I share your website and show these videos in a DOE webinar I’m putting together for teachers? I’m the elementary math specialist for the GA dept. of ed, and these videos demonstrate a number of useful ideas (tee hee).
Thanks,
Turtle
Sure you may show them. Hope your webinar goes well.
It went well. The webinar team loved the videos. Our MS and HS teams are going to use them in their webinars now. Nice work. Thanks for sharing.
Came from HN. I do wonder if the problem isn’t related to the notation on the highway sign. I would love to see the class experiment repeated where the image is photoshopped so distances show up like ‘regular’ fractions (ie no / slash but horizontal line)
Hi John. I can’t say with complete certainty but I believe that students understood that the numbers were fractions that represented distances. In retrospect, it would have been a good question to ask as a follow up.
Thanks Robert for your thought-provoking lessons and for the forum you provide. We’ve been exploring the highway sign lesson in our fourth grade classes. We had them draw a picture of what the road would look like, scaling 1 mile to the length of a 1 unit fraction tile. The biggest issue was understanding that the exits were measured from the sign. Once they got the hang ofi it they were able to use the 1/2 and 1/4 tiles to accurately space the exits. Then we had them turn the road into a number line and place the exits there. We also investigated what the road would look like if a mile was scaled to one inch.
Their pictures were interesting. Some had the exit roads crossing the highway and we needed to add traffic lights. Some roads exited left and others right. We talked about why the information was important for drivers and gave them toy cars to drive along their roads. We found other examples of signs and let them continue to work on the activity.
I think it will be interesting to have them create their own signs, with exits not limited to quarters.
Joe, thanks for sharing this excellent suggestion. I am glad you found an opportunity to address this misconception and help students make sense of what they were learning. It sounds like the students really benefited.
Your sheep, dog, and shepherd video was great to watch. I was sure I knew those students in the video as my own. Thank you for posting these educational videos.
I read some of the comments below and agree that the freeway problem was perhaps, a little too much to ask a student to conceptualize withouth some prior knowledge.
Perhaps changing it to the following:
In a school race, the rules were to run until the teacher blew the whistle, at which time all students had to stop. When the whistle blew, Jose had run 1 1/2 miles and Maria had run
1 1/4 miles. How far apart were Jose and Maria from each other when they stopped?
Just an idea that I will definitely put to the test with my 6th Graders now that my school/district is embarking on the CCSS.
Thanks Victoria. Yes, I definitely made an assumption that the problem’s context was negligible. I would hope that at the very least, introducing this problem would allow for a discussion on what information the sign is actually conveying. That didn’t happen in the video but it could happen in the classroom.
Let me know how your idea goes.
Robert,
I had the opportunity to attend your workshop in Fort Zumwalt. Part of your presentation included a video showing students who were asked to answer the highway question. Your video showed several student responses to both the highway problem and then, you followed it with a video showing student responses to the basic fraction problem. I was wondering if that video is located anywhere on your site? ( as I would like to share it with my department as “proof” as to why we must make more connections in our math classrooms),
Hi Stacey,
Maybe I am misunderstanding your question but doesn’t this post contain the videos you are looking for?
Great post! Thank you for these thoughts and reminders! This is my goal in teaching mathematics and it’s so helpful to remember as we come to the end of the year!
You are welcome Ashley. Hope your year ends strong.
Great stuff here Robert. I like the video that really nails home the point. This reminds me of my students adding 1 feet 6 inches to itself or 1 feet 6 inches times 2 and coming up with 3.2. Which leads to an opportunity for students to explain what error was made. I hate to say it, but common sense is not so common anymore, but our job as teachers is to let the students that understand it explain it to the class and their peers and facilitate those discussions.
Thanks Martin. My hope was that this video would make it easier to demonstrate that reality.
I’m a bit surprised that anyone would be surprised by these results. This is the very crux of what is missing from US mathematics education: the realization that we’re creating countless numbers of kids who think that to do math is to mindlessly compute without any thought given to why we would ever do a particular computation outside of a worksheet in school. How many of us have heard how many times from how many kids, “I know how to do the math; it’s just these word/story problems I don’t get”?
You wonder how it is conceivable that so many students have (seemingly) never been in a car on a road with signs like those in this lesson at which time they wondered, “How far from Exit 11A to Exit 11B?” Maybe it has to do with the number of kids who never look up from their electronics when they’re passengers (my son being a classic case in point; he’s finally paying the price now that he’s driving without me to navigate). But I suspect that it’s just an extension of a long-standing problem that has its major roots in our entire school culture in general and our math classroom culture in particular.
Thanks Michael. Admittedly, it is more obvious now, but when it took place about 7 years ago, it certainly was not. Definitely have more perspective with experience.
Thank you for your insights. Your lesson and video are fantastic and I look forward to sharing them with my colleagues. This lesson is a great progression into the 6th grade content with absolute value. I appreciate you sharing your thoughts!
I really appreciate the kind words Jill. My goal for this blog is to provide resources that I would have found useful moments earlier when I had no clue this issue existed or was needed.
I know this was posted 3 years ago, but….aren’t we supposed to prepare kids for the “real world” they will eventually inhabit too? My kids want to know how to figure out how to get around when they are old enough to drive. They want to know how grown ups do their work. I agree that putting things into contexts that are directly applicable to current situations is valuable, but so is explaining that some parts of math are really useful tools for us to navigate our lives when we don’t have parents anymore. That’s part of the goal of education in my mind. Also, sometimes our contexts seem contrived (I don’t care how many cups makes your height example), but what if we knew what the original questions was that fractions answered? What challenge was arising in history that required people to split numbers apart? Can they see how it might be really hard to live without fractions? What would we not be able to do anymore? So how does someone just “make up” this idea of fractions? That’s called mathematics! And I hope we share more of that with students too. 🙂
Thanks Shelley. I think where we all agree is that we want students to make sense of whatever mathematics they do and to see mathematics as a tool they can use to answer their questions. Certainly whatever one child holds to be “real world” or “relevant” will be different to another. Thanks for adding to the conversation.
Thanks for sharing this article / lesson, as that has been a big focus during my math class. Can my students transfer their procedural and conceptual understanding to a real life problem. Therefore after reading this, I did something similar with my class. The results were interesting. Not only to see those children who gave up as soon as they saw a written problem (even though they do these regularly in class), it identified the child that couldn’t do any, and then the child that could do the written but not the procedural problem. So a whole mixture of results for me to think about, however, for the majority, i think my students don’t understand the actual concept well enough to transfer that to solving a real world problem. I shared this information with them so they can see why it is so important to be able to apply their math knowledge. They found the results interesting. Thanks for sharing another great lesson.
I’m glad this gave you a useful context to use with your students. The main idea, as you realize, is not that these particular problems are so special, but the general idea that we want to use contexts and problems with students that are more likely to bring out misconceptions in a manner that we can deal with them.
Do students at this age realize that the freeway signs are telling you how far you are away from each exit? I could imagine that some students pay attention to those signs while driving on the freeway, but I could also imagine many students having never even thought about what those signs mean. I could also imagine many students, who rely on public transportation, rarely ever even being a passenger in a car on the freeway. So I am curious if that was explained to the students before giving the question, or if they were meant to deduce that information.
I see you addressed this in a previous comment. Thank you.
No problem.
I appreciate your videos! My co-worker and I recently showed the shepherd problem to all of our teachers in grades k-5. It was very powerful to show them what methods like C.U.B.E are doing to our students. We even had some teachers go back and make their own problems up to see what students would do. It was very eye-opening for them!!!!!! (And it gave the why we need to change)
Thanks Alice. I think that there can never be enough examples of WHY we need to change. There are plenty of resources to tell us WHAT to do and HOW to do it. Never enough though about WHY. Glad you found this valuable.
This might be a great example to discuss – the I Wonder and I Notice and then do some work on the clothesline. Perhaps using whole numbers first and then changing the problem to fractions and perhaps decimals. I used to tell my high school students, “The rules don’t change, just the numbers do.” Moving through the different numbers on a clothesline may help with the ‘why’ before using their procedure on an application problem.
We also need to do our K/NTK.
That is our knows and our need to knows.
I have also found that my students have difficulties when they are given any problem that has fractions in it. This is because they do not have a solid foundation in fractions.
Really have to help them to get over this problem.
Suggestions are welcome.
There is an opportunity to peek at absolute value here. Student A is wrestling with going past zero into negative fractions, but distance is always positive. This might freeze many students at first. Lots of room to open this question up & make connections. Good low floor high ceiling group activity. Thanks for posting!
Yeah, these problems are good at opening up Pandora’s box and point out all the opportunities.
Fractions seems to be the most troublesome topic for most students. It is even very difficult for some adults, I once worked with some student teachers and lo and behold you probably will not believe this but these student teachers were when they were adding fractions were adding the numerators together and then putting the answer over the sum of the denominators. So if these are the folks teaching our very young learners then no wonder these students suffer so much,
Having nightmares when asked to do anything on fractions,
My question how can we eliminate this fraction phobia
I believe that one step is helping people see it as more than just randomly banging numbers together and develop conceptual understanding. I can empathize with all teachers in that it’s so challenging to be teaching students in ways we were not taught or didn’t understand.
Math is really something more than banging numbers. For someone to understand math concepts they need to understand that math is not just about numbers. When characterized with real life situations becomes challenging and explain itself in a more meaningful way.
Excellent post! I strongly believe that the objective of education is no other than showing the World to our students. It doesn’t matter if we need a complete lesson to talk about highway signs, miles, fraction “shapes” (By the way, I hate mixed numbers, as the notation disagrees with the algebraic one). Students may not pay attention to the signs, until they know what they are, thanks to the math lesson.
We are working with polygons (Parallelograms, Rhombi, Rectangles, Squares). My students can solve multistep equations and they know a square has 4 equal sides. I am amazed how I can give students a diagram of a square with binomials at opposite sides defining length of the side, and some do not know that you set the two expressions equal to each other to solve for the variable, and later substitute it into the binomial to find the length of the side.
I totally did NOT understand that until I had been teaching for many years. I know from personal experience that it can be easier to be a robot than to actually understand why it works.
Great post. I am often overwhelmed by the work that continues each year with a new group of students. I am grateful that classes like these are making the rounds so we can all work together to change things for our students. Thank you!!!!
I like the thought that there needs to be a balance between procedural skills, fact fluency and conceptual understanding. This type of articulation is very good in reaching out to teachers and helping us learn together on how to teach math.
I also like that balance. It comes straight from the Common Core State Standards and has been useful for me in understanding how we make deep learnings.
Thank you for sharing this post! It is mind boggling on one hand that students cannot do this road sign problem. Yet it is totally understandable on the other hand because students are not given contextual problems to solve often enough in day to day classroom settings. This so clearly explains what I observe in my role as a math coach, students can calculate but not necessarily reason when they solve problems. Part of the issue is that curriculum is loaded with math problems that lay out sets of numbers to be calculated. Getting to your point, that if students can correctly perform calculations, they are proficient in their procedural understanding. We as educators need to stop thinking that procedural aptitude equates to conceptual understanding.
My goal for sharing this has been to encourage the kind of self-reflection you described. There’s a whole lot we have to dig in to so we can move forward and prevent this from happening.
Hi Robert,
I hope this can be useful.
I teach in a Professional Institute (from 14 to 18 yo students) in a bad socio-economic environment, and most of my students have lots of problems with math and my first goal is to show them how could it be full of beauty and then, of course, to teach them how to use it in everyday life.
Note that in my country you can’t find a street sign like that: we never use fractions to indicate distances (maybe because drivers could never understand them…) but there is another problem: at school, when we write 1 1/4 we always use to mean 1 “times” 1/4 and if we want to mean 1+1/4 we have to write it expressly. Instead, when we are talking about time we often say 2 “and” 3/4 to mean 2 hours “plus” 45 minutes, but only in that circumstances. Many times in everyday life math is used in a mixed way, partly in math language and partly in italian language, and this leads sometimes to misunderstandings, but not always, as we’ll see.
That being stated, I tried to give your application to my students, in one class talking about distances and in another one talking about hours (“we’ll meet at “una e un quarto” and we’ll leave at “una e tre quarti”. How long shall we spend together?”). In the first case I had to wait about 10 minutes for the answer and about 60% got the wrong one, in the second one the majority of them answered in few seconds and only about the 5% couldn’t solve the problem. Curious.
Finally it was very interesting working with them on how math is used in our everyday life and on how to avoid… crossed wires.
Thank for your work, and sorry for my “not-enough-practiced” english 🙂
Carlo
This is really interesting. I hadn’t thought about how fractions were represented differently in other languages. I love opportunities to get kids thinking though and questioning what they think they know (and for that matter what we think we know as their teachers). I appreciate you writing up this reflection.
P.S. Your English is basically perfect and FAAAAAAR better than my Italian. I wouldn’t have realized it wasn’t your first language if you didn’t say so.
I like to find a balance between relatable word problems and ‘real-life’ that they may or may not know already (such as the street signs. This example is a great way to introduce students to the skill of reading street signs and direct teaching how to put into context the application of the skill.
I have had this happen where students can’t put the procedural problem into the context of a word problem. The next day, I give them the procedural problem, which most get correct. Then I review the real-life problem with them. In this case, I would have suggested that they draw a picture of the situation to help them see that they could use a number line to solve the problem. It is difficult at times, but I like learning from these situations myself and let the students know that they are teaching me as well.
Thanks Michele. I know that this experience really helped me see a gap that I didn’t know was there. I was much more sure about it being important to close, and much less sure about how exactly to close it.
Thank you Robert for sharing this post with us, it made me think about how can I really show my students the use of Math in their daily lives, I teach first graders and I´ve been trying to expose them to daily live situation problems in which they can apply what they´ve learnt, but your post made me think that next year I´ll try to make them come up with problems where they can actually use what they´re learning, I will probably start with something easy additions and subtractions so they can get use to it. Maybe if I manage to make that a routine in our Math class they will be able to solve problems easily applying what they learn in class.
Dan Meyer shares a metaphor that I’ve found to be particularly useful in centering myself for what you described. He says that if math is the aspirin, then what is the headache? For example, why would we ever count by fives or tens? How useless is that?
Well give someone a pile of pennies and ask them to count them and watch them keep losing track. Then making groups of fives and tens seems like the aspirin to the headache.
Finding those headaches and giving them to students is often very rewarding.
I am tutoring my grandson who has learning disabilities. The question what is the purpose of math knowledge for a person like him is always on my mind. Your highway example is exactly what i am talking about. For him the goal it is not the “manipulation of fractions” as a skill, it is the understanding of what kind of manipulation he needs to perform. How to perform the needed manipulation is an easier intellectual task.
I absolutely get this. It’s not just computation but also knowing what to compute and why.
I was a student who was very good at the procedural fluency, but I had not conceptual understanding in many areas. I learned this when I was teaching! I have had some minimal training for teaching conceptually at the lower elementary level, but was unsure of what that would look like at the upper levels. This is helping to be a great resource, and to get out of my own way of how I used to teach high school math (procedurally.) I can’t wait to share with some colleagues and encourage them to step out of their comfort zone to do what is best for our kids!
Realizing that gap and then working to do something about it is huge. I would go as far as saying that anyone who thinks they have no gaps likely either doesn’t understand the math deep enough to know what they don’t know or they’re lying to themselves.
It’s one of those things where the more you know, the more you realize that you don’t know it all.
What an amazing resource! This definitely gives me a clearer picture between students’ procedural versus conceptual knowledge. I learned that we have to work on students conceptual knowledge and this is something we need to begin exercising in the early grades so they can relate the math to world experiences!
I’m glad this was helpful. Thanks!
I’m curious if the students would have been able to answer the question if the context was something they could relate to. Grade 5 students aren’t drivers. The highway signs are not something they have had to make sense of yet. And with no units on the sign, they didn’t have a clue that the numbers represented distances. If you asked them the same question about two distances that they could see in the classroom, I wonder if more students would have been able to find an appropriate answer.
These are the right things to be curious about. Usually I’m more aware that there is a problem and less clear about why the problem exists or how to fix it. I would absolutely look into each of your wonderings and experiment with them.
I think that wondering helps. Maybe this helps us understand our students thinking better: Just as there is a distinction between complex and complicated, maybe there is a distinction between understanding that this is a math problem vs. translating this into a math problem.