How Many Laps Is A 5k Race?

 
You are training to run in a 5k (5000 meter) race and want to practice by running laps around a local park.
 

• How many laps around the park do you have to run to go 5k?

 

These questions may be useful in helping students down the problem solving path:

• How far are you running?
• How can we figure out how long the park sides are?
• What information do we need to know to determine the park sides’ lengths?
• What tools will we need to do this?

After students have come up with the number of laps in decimal form:

• What does the whole number represent?
• What does the decimal part represent?
• What distance does that decimal part represent?
• How can we determine starting and stopping points to complete exactly five kilometers?

 

Students may not be familiar with what a “5k” race is, so they may need to ask about and learn that it is 5 kilometers or 5,000 meters long.

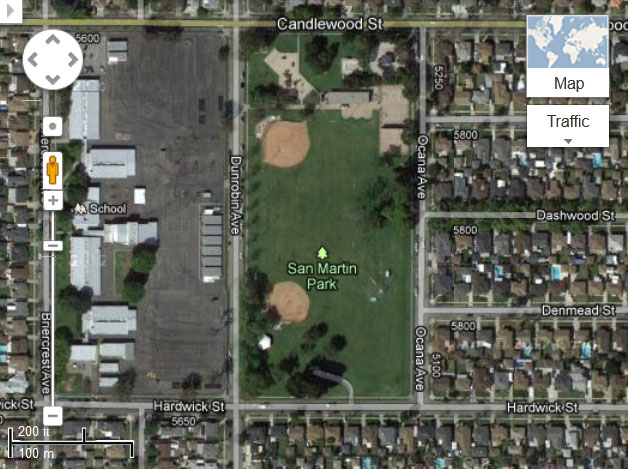
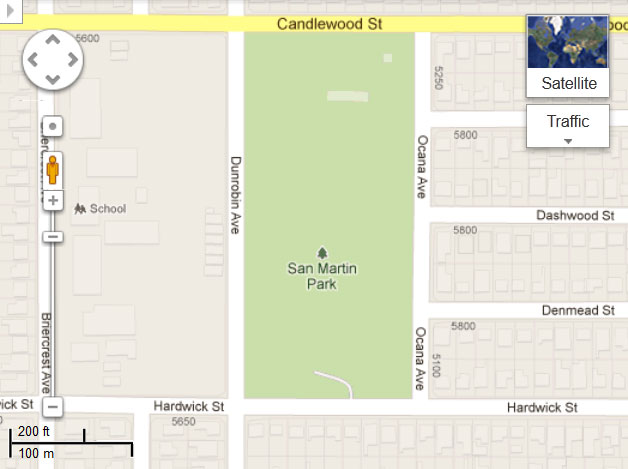
Two maps have been provided: satellite map and road map

The park is not exactly rectangular so you can adjust the problem’s difficulty by assuming that it is and/or allowing students to round their measurements.

When I calculated the park’s dimension using a ruler and a printed copy of the road map with scale, my measurements were:

• Dunrobin Avenue about 304.1 m
• Candlewood Street about 140.8 m
• Ocana Avenue about 304.1 m
• Hardwick Street about 138.8 m

Accordingly, based on my measurements, one lap is 887.8 m.  Dividing 5000 m by 887.8 m, gives you an approximate answer of 5.63 laps.

At this point, I would encourage students to explain what “5.63” represents.  Some students may not know if it is 5.63 km, 5.63 m, or 5.63 laps.  Once the units are understood, it is definitely worth exploring what the “5” and “.63” represent.  Students should be able to explain that the 5 represents five complete laps.  The 0.63 is more complicated.  Students may state that it is 0.63 laps, but in the context of the problem, where would the runner have to start and stop to have run 0.63 laps?

There is more than one way to determine where the starting and stopping points would be (and it partially depends on what assumptions were made earlier about side lengths).

• One strategy is to convert 0.63 laps back to meters by multiplying by the length of a lap or 887.8 m.  This gives about 559.31 m.  Students can then subtract alternating street lengths until they have less meters left than they can subtract.  So, if the race starts at Candlewood St and Dunrobin Ave and heads towards Hardwick St, 559.31 m – 304.1 m leaves 255.21 m.  Continuing down Hardwick St. to Ocana Ave takes off another 138.8 m leaving 116.41 m.
• Another strategy (which works if opposite sides are equal lengths) is to realize that half a lap is 0.5, so 0.63 – 0.5 leaves 0.13 laps.  Converting 0.13 laps back to meters gives about 115.41 m.  Note that it is one meter less than the other measurement because I assumed opposite sides are equal lenghts and as a result, the length of Hardwick Street was averaged to be one meter longer at 139.8 m.

We are still not done yet because while we know we need to run 5 complete laps and 1 half lap, we also need to run about 116.41 m more.  If we run this portion along a short side, we will need to go approximately 84% of the way.  If we run this portion along a long side, we will need to go approximately 38% of the way.

There are many great opportunities for math discussions with this lesson.  Good luck!
 

• Satellite Map

• Road Map

• CCSS 4.MD.3 Apply the area and perimeter formulas for rectangles in real world and mathematical problems. For example, find the width of a rectangular room given the area of the flooring and the length, by viewing the area formula as a multiplication equation with an unknown factor.

 

• Google Maps
• Nike Inc.