Is Gas Cheaper With Cash Or Credit Card?

 
Some gas stations charge lower prices for customers who pay with cash instead of credit cards.  Some credit cards give a cash back rebate for purchasing gas.
 

• Is gas cheaper with cash or credit card?

 

These questions may be useful in helping students down the problem solving path:

• How much do you save by paying for gas with cash?
• How is the amount of the cash back rebate determined?

 

The picture below shows a gas station with separate prices for “Cash / 76 Card” or “Credit / Debit” card.  Ask students, “How much do you save by paying for gas with cash?”  You want to establish that initially, it appears that paying with cash will save you money.  Students most likely will say “10 cents”.  This is a good opportunity to practice Math Practice 6 and make sure they “are careful about specifying units of measure.”  Specifically, unless you are buying exactly one gallon, you will save more or less than 10 cents.  If students use precise language, they should state that they would save “10 cents per gallon”.

For the purposes of this activity, we will compare the total cost of paying with cash versus paying with a credit card that gives a percentage of the purchase price back as a rebate.  Students may come in with some knowledge about how credit card cash back rebates work.  To bring this information to light (and address any potential student misunderstandings ) be sure to ask them, “How is the amount of the cash back rebate determined?”

Acknowledge what students say but state that the credit card(s) we will be discussing come(s) from American Express and show them the first image below:

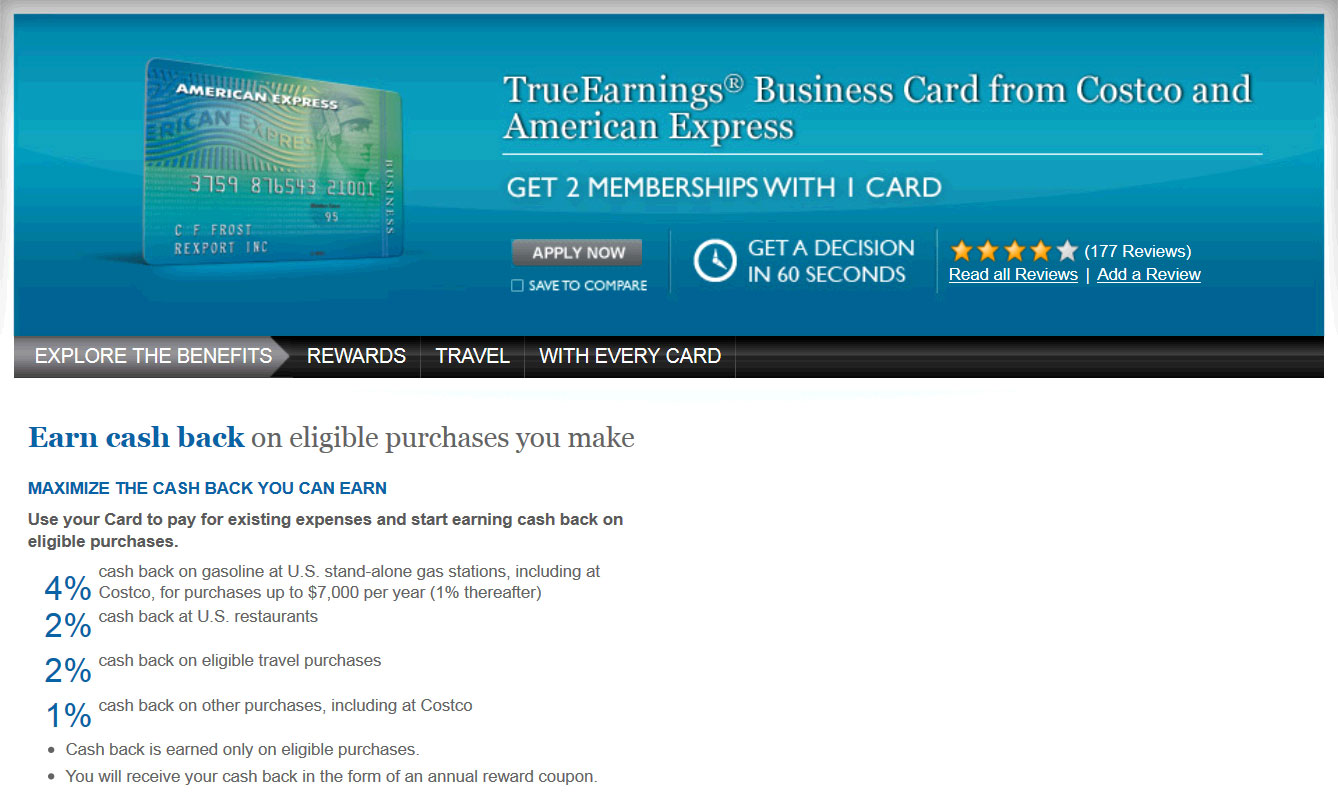
Give students time to read the page and determine how the rebate program works.  They should notice that customers who use this card will receive “4% cash back on gasoline at U.S. stand-alone gas stations, including at Costco, for purchases up to $7000 per year (1% thereafter)”.  At this point, share with students that we will assume that we will spend less than $7,000 per year and therefore always earn 4% cash back instead of 1%.

At this point, students should have enough information to answer “The Challenge” question.  Is gas cheaper with cash or this credit card?  Here are the calculations:

So, using a credit card that offers 4% cash back on gasoline purchases saves us more than the 10 cents per gallon we save from paying with cash and it is therefore cheaper to pay with credit card.  Note that the calculations have been rounded to the nearest cent.

As an extension, here is a slightly different version of the problem with the non-Business version of the card that only offers 3% cash back (for the first $4,000 in gas purchases).  Would this card still save you enough money to use it instead of paying cash?

Here are the calculations:

So, using a credit card that offers 3% cash back on gasoline purchases still saves us more than the 10 cents per gallon we save from paying with cash and it is therefore cheaper to pay with credit card.  Note that the calculations have been rounded to the nearest cent.

Here is a list of all the assumptions I noticed I was making during this lesson:

• You pay off your balances in full each month and don’t accrue interest or monthly service fees.
• There is no annual fee.
• You have a Costco account already.
• You are spending less than $7,000/$4,000 per year on gas (though it would be an interesting extension problem to determine if that is a reasonable assumption as well as how the 1% thereafter would affect the overall savings)
• We are ignoring that we don’t get the rebate back until the end of the credit card year and treating it like it was instantaneous cash back.
• We have the cash available to pay with cash if we wanted to (so not having that much money in my wallet is not an issue).

 

Thanks to Mathalicious (another great source for real-world problem based lessons) for finding the photo below.  Will this be an obvious choice for your students?

 

• CCSS 7.RP.3 Use proportional relationships to solve multistep ratio and percent problems. Examples: simple interest, tax, markups and markdowns, gratuities and commissions, fees, percent increase and decrease, percent error.

 

• American Express TrueEarnings Card
• American Express TrueEarnings Business Card
• Mathalicious