How Can We Make Stronger Passwords?

 

• How effective is each password requirement in making a password take longer to hack using brute force?
• What is the longest amount of time it would take a computer to hack your password?
• What recommendations would you make regarding password requirements so that they are as secure as possible?

 

These questions may be useful in helping students down the problem solving path:

• What kinds of characters can you use for a password?
• What is a guess for how long it would take a computer to hack your password that is too low?
• What is a guess for how long it would take a computer to hack your password that is too high?
• What is your best guess?

 

As shown in the video, one common type of password hacking (or cracking) is called “brute force” and involves using a computer to try every single possible combination of characters until it enters the correct one.  For example, if a password was one character long and could only be an English lowercase letter, then there would only be 26 possible passwords (“a” through “z”).  If a hacker tried each of them, he or she would be guaranteed to figure out the password by the 26th attempt.  As the video mention, “the more complex the password, the longer it’s going to take to crack.”

Where the math gets interesting is figuring out what password requirements make them more “complex,” or more specifically, are most effective in increasing the total number of possible passwords a hacker has to try.  For example, if you took the previous scenario and now allowed lowercase and uppercase English letters, there are now 52 possible passwords (“a” through “z” and “A” through “Z”).  However if you instead required passwords to be two lowercase letters long, there would now be 676 (26^2) passwords “aa”, “ab”, “ac” through “zy” “zz”).  That is because there are 26 passwords that begin with “a”, 26 more passwords that begin with “b”, etc. all the way through “z”.

Potential password requirements include:

• May use lowercase characters
• May use uppercase characters
• May use characters from other languages (for this lesson, we will not allow this)
• May use numbers (0 through 9)
• May use symbols (for this lesson, we will limit it to the following 8 symbols !@#$%^&*)
• Minimum and maximum number of characters

 

You may want to begin with students working as a whole class to agree on a certain set of password requirements and then calculate the total number of potential passwords based on those requirements.  There are a number of methods available to figure out the total number of potential passwords.  A tree map is very effective at developing conceptual understanding when there are very, very few possible characters.  Permutation formulas will work as well.  Eventually they will lead to a generalized formula to figure out the number of potential passwords similar to:

(number of possible characters) ^ (number of characters in the password)

 

For example, if a password has 8 characters and lowercase, uppercase, and numbers are the only characters allowed, the total number of potential passwords would be:

(26 lowercase characters + 26 uppercase characters + 10 numbers) ^ 8 characters in the password

(26+26+10)^8 = 62^8 = 218,340,105,584,896 ≈ 218 trillion potential passwords

 

Perhaps it goes without saying, but this is not the time to have students calculate the totals by hand.  The time spent calculating totals by hand will reduce the time students have to consider how the requirements affect the total number of potential passwords.  Once there is understanding and agreement as to how to calculate the total number of potential passwords, let students play around with the different password requirements to see how they affect the total number of potential passwords.  For example:

• think of a strong password they have heard of and calculate how many other passwords have the same requirements.  Note that the student does not need to share the actual password, just the requirements.  For example, he or she can state that it has # characters, has lowercase letters, no uppercase letters, and numbers.
• do the same for a classmate’s password requirements and verify that they got the same results.
• calculate the total number of potential passwords based on the password requirements they use for one of their own passwords.

 

At this point, students may have a false belief that the seemingly large total number of potential passwords implies that the passwords are secure.  So, have them guess how long they think it would take for a computer to guess their own password.  You may need to ask them for low and high guesses if they have trouble coming up with an answer, allowing them to say, “My low guess is at least a year and my high guess is a century.”

Where the lesson starts to get very real is when you show them the article (click on the “Download files” button towards the bottom) about how quickly computers can check passwords.  The image below shows the first page of the article with a computer that can “cycle through as many as 350 billion guesses per second.”  That adds a serious dose of reality because while 218 trillion potential passwords seemed like a lot, at 350 billions guesses per second it can be hacked in less than 11 minutes.

 

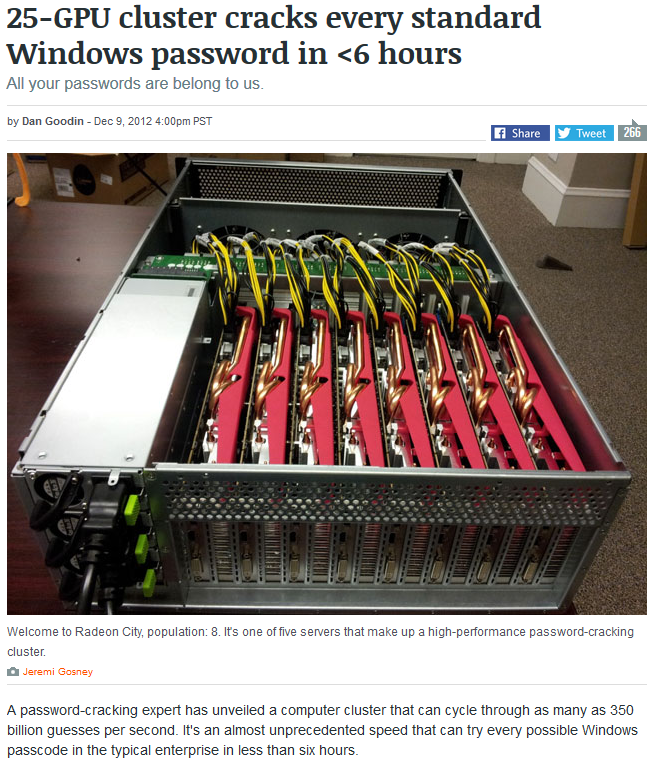
Have them now calculate the amount of time it would take to guess a password with the requirements they came up with earlier.  Depending on what they chose, they may be surprised that many of them can be guessed in less than an hour.  Give them additional time to adjust their password requirements.  Eventually they should come to the conclusion that the single most important factor in making a password more complex is the password’s length.  For example, the password “ThisIsMyLongPassword” has 20 characters and uses only lowercase and uppercase letters.  Accordingly, to calculate the total number of potential passwords that have the same requirements, you get 52^20.  There are approximately 2 x 10^34 passwords with those requirements and it would take 1.8 quadrillion years to crack it via brute force on that computer.

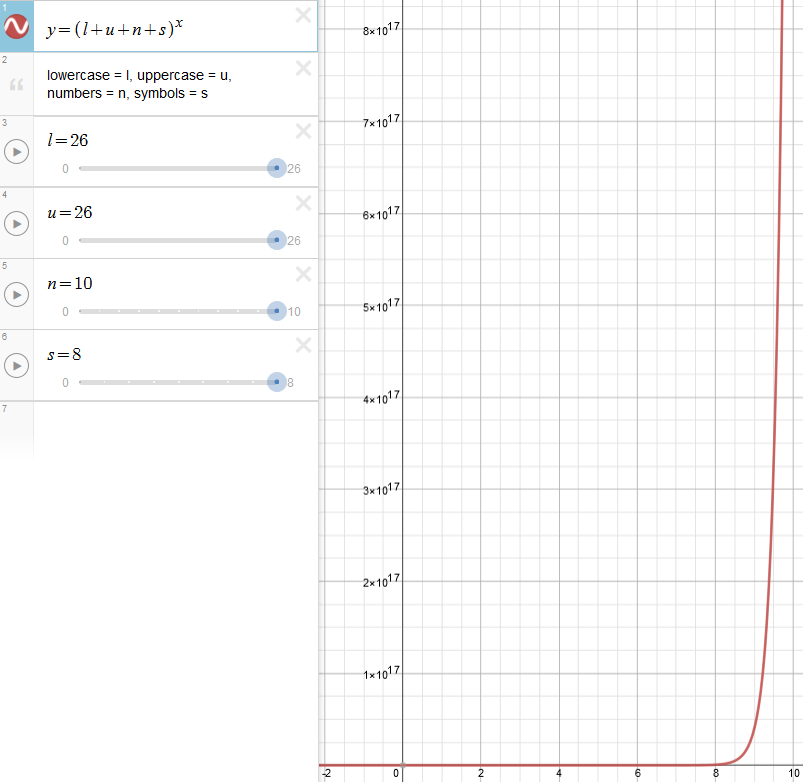
This Desmos graph has adjustable sliders to shows a visual representation of how the total number of potential passwords change based on four requirements:

• lowecase letters (26 potential characters)
• uppercase letters (26 potential characters)
• numbers (10 potential characters)
• symbols (8 potential characters for this example)

 

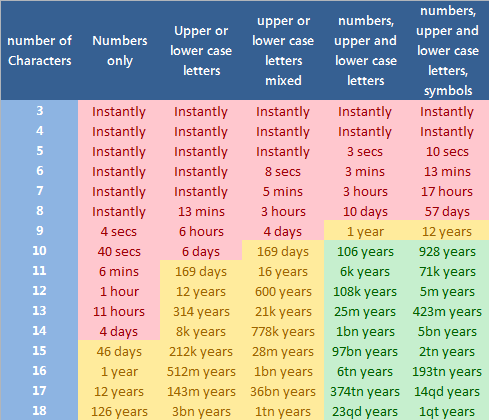
The chart below uses data from computer speeds in 2022 and makes a nice visual to help people see which factors matter more.

 

It might be interesting to compare the data above to a similar chart using data from computer speeds in 2010 so you can see how much times have changed with increased computing power.

 

It is worthwhile to note why this type of hacking is not more common in real life:

• Many websites limit the number of times you can enter incorrect passwords before the account is locked.  Not all websites do this and the Apple celebrity photo hacking is an example where no limits on incorrect passwords combined with weak passwords were the problem.  The article states, “Presumably, hackers breached the accounts of celebrities by writing brute-force software programs to attempt many passwords for email addresses.”  Clearly their passwords were not strong enough.
• Many websites have other software that detects an abnormally high volume of website traffic and shuts access down.
• Hacking anything that is not already on your computer (such as a password protected file) requires information to go back and forth online, which takes time.

 

Finally, one sobering fact is that the article on the password guessing computer was written in 2012.  You can be certain that it won’t be long before 350 billion passwords per second is considered slow.
 

• CCSS 7.SP.8 – Find probabilities of compound events using organized lists, tables, tree diagrams, and simulation.
• CCSS 8.EE.1 – Know and apply the properties of integer exponents to generate equivalent numerical expressions. For example, 3² × 3^-5 = 3^-3 = 1/3³ = 1/27.
• CCSS S-MD.7 – Analyze decisions and strategies using probability concepts (e.g., product testing, medical testing, pulling a hockey goalie at the end of a game).
• CCSS S-CP.5 – Recognize and explain the concepts of conditional probability and independence in everyday language and everyday situations. For example, compare the chance of having lung cancer if you are a smoker with the chance of being a smoker if you have lung cancer.
• CCSS S-CP.9 – Use permutations and combinations to compute probabilities of compound events and solve problems.

 

• Chris Robinson
• Chris Haralson – “How To: Crack a Password-Protected Zip File”
• Desmos
• Password Security Chart