- Which payment option saves you the most money?
- How can we figure out how much it will cost for a whole year if we pay monthly?
- What information do we need to know to figure this out?
At the secondary level this could be done as linear equations or systems of equations. Graphs for each theme park have been provided. Some things to note:
- The x-axis measures the number of months
- The y-axis measures the total amount paid in dollars
- Each pass has its own color (i.e., Disneyland Premium is red and Disneyland Deluxe is purple).
- I have listed two linear equations for each pass (except Universal Studios Hollywood’s Buy a Day which has no monthly payment option): one for the single annual payment and one for the monthly payments.
- The single annual payment is represented by a solid line because you have paid the same at every moment of the year.
- The monthly payment plan is represented by individual points. Technically it is a continuous step function (as opposed to a discrete function) because instead of going up linearly, the total amount paid stays exactly the same over the course of the month until it jumps up when the next monthly payment is paid, repeating the process throughout the year. However when I graphed it as a step function, it was very hard to read. So, I left it as individual points.
Some potential confusion areas to be aware of:
- Students may try to compare the different tiers of plans to each other. For example, they may compare the Disneyland Premium pass against the Disneyland Deluxe pass. We are only comparing how much each plan costs when paying annually versus monthly.
- Students, especially younger ones, may be challenged by determining what information in a chart is important. For example, in the Disneyland example below, do the number of days you can use the pass or the discounts you get affect the results? Students might think they do.
Disneyland
Disneyland has four plans to choose from: Premium, Deluxe, Southern California, and Southern California Select with pricing listed below.
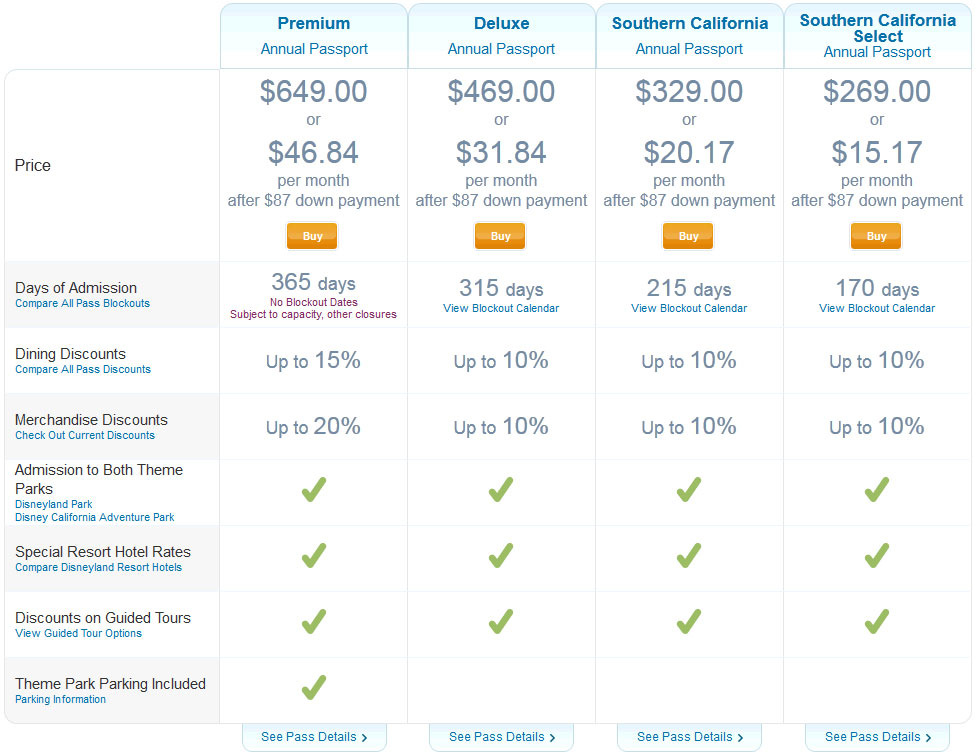
Since there are twelve monthly payments, the total cost for monthly payments will be:
total cost = 12 * monthly payment + down payment
The chart below (which is easier to read if you click on it) gives the full breakdown.
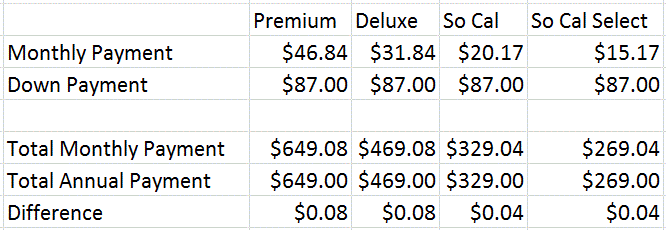
For the Premium and Deluxe passes, you save $0.08 by paying annually. For the Southern California and Southern California Select passes, you save $0.04 by paying annually. This difference is obviously very small, and students could potentially argue two ways. Students may say that paying annually saves the most money (4 or 8 cents), however that is less than the amount someone would earn by keeping the money they would have used for an annual payment in a bank account that collects interest. So, as long as the students have a good justification, I would accept either answer.
If students graph the payment options, it should come out looking something like the graph below.
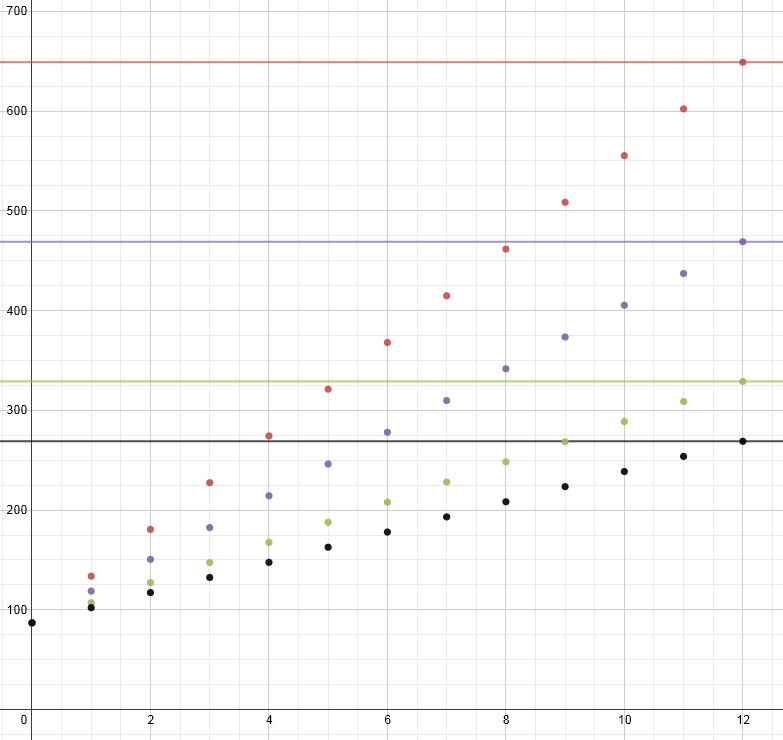
Here are some of the ideas I hope would come out from a discussion about this graph:
- All the monthly payments have a common y-intercept at (0,80) because you have to make an initial down payment of $80 before the first month begins.
- Their slopes differ because the monthly payment amounts are different.
- By month 12, the monthly and annual payment options appear to intersect because their values differ by pennies.
Universal Studios – Hollywood
Universal Studios in Hollywood has three plans to choose from: Premium Star, No Black-Out, and Buy a Day with pricing listed below.
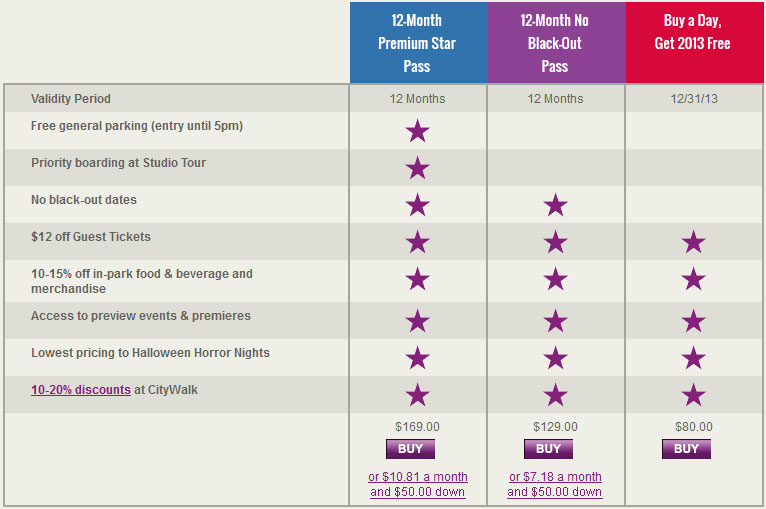
Full disclosure – I have modified the above image to make it fit better online. It said “one low down payment of $50 while spreading the remainder of your total over the next 11 months” below the chart so I moved some of that information into the chart.
Since there are eleven monthly payments, the total cost for monthly payments will be:
total cost = 11 * monthly payment + down payment
The chart below (which is easier to read if you click on it) lists the total costs for the annual versus monthly payments.
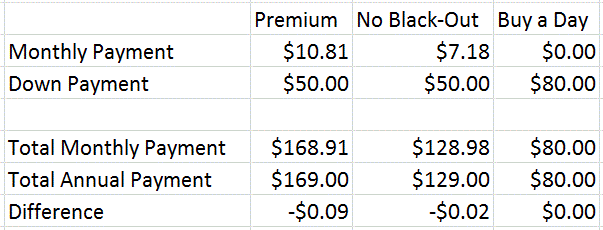
For the Premium and No Black-Out passes, you actually lose $0.09 and $0.02 by paying annually. So for those two passes, you save the most money by paying monthly. For the Buy a Day pass, that is a pass where if you pay $80 for one day, you get the rest of the year free. As such, it is essentially an $80 annual pass with no monthly payment option.
If students graph the payment options, it should come out looking something like the graph below.
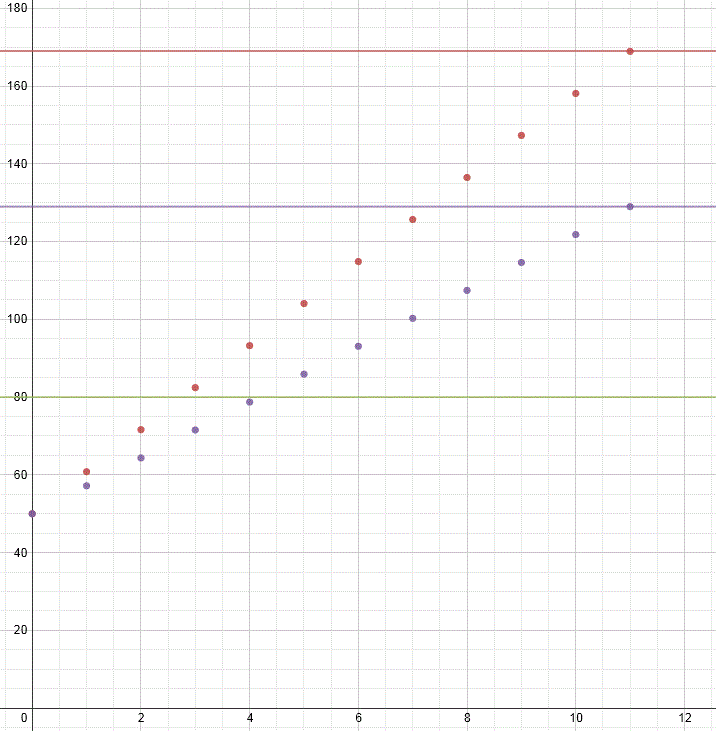
Here are some of the ideas I hope would come out from a discussion about this graph:
- All the monthly payments have a common y-intercept at (0,50) because you have to make an initial down payment of $50 before the first month begins.
- Their slopes differ because the monthly payment amounts are different.
- By month 11, the monthly and annual payment options appear to intersect because their values differ by pennies.
- There is no payment in month 12 because your down payment counted as your initial payment.
Universal Studios – Orlando
Universal Studios in Orlando has three plans to choose from: Power, Preferred, and Premier with pricing listed below.
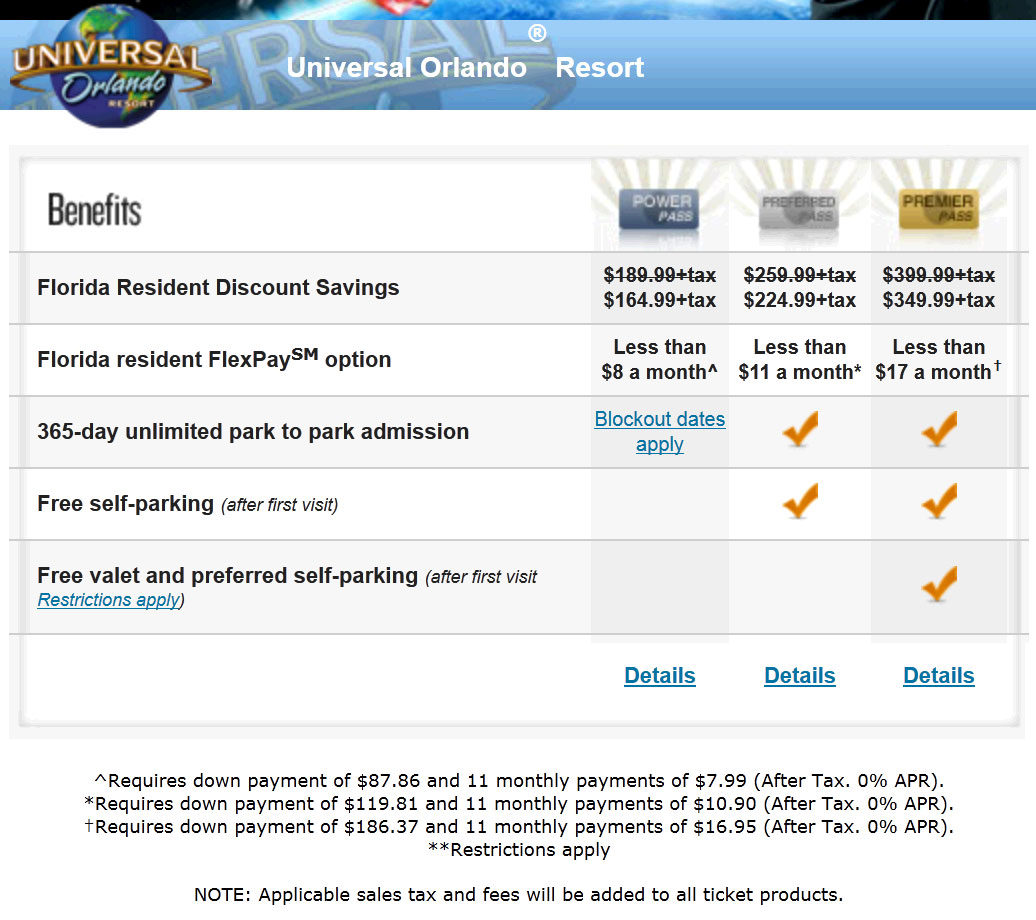
Full disclosure – I have modified the above image to make it fit better online. There were many rows in the table that had additional pass benefits. It made the table too long so I erased them.
Since there are eleven monthly payments, the total cost for monthly payments will be:
total cost = 11 * monthly payment + down payment
The chart below lists the total costs for the annual versus monthly payments.
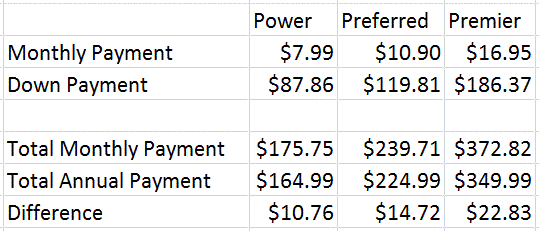
The Power, Preferred and Premier passes cost $10.76, $14.72, and $22.83 more, respectively, if you pay monthly instead of annually. As such, paying annually saves you the most money.
If students graph the payment options, it should come out looking something like the graph below.
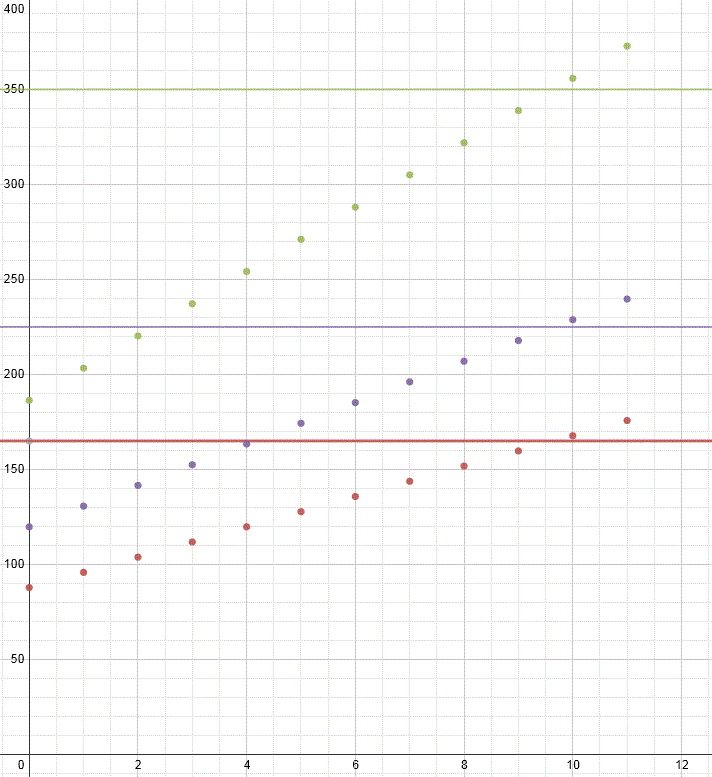
Here are some of the ideas I hope would come out from a discussion about this graph:
- None of the monthly payments have a common y-intercept because their initial down payments are all different.
- Their slopes differ because the monthly payment amounts are different.
- By month 10, the monthly payment is now more than the annual payment.
- There is no payment in month 12 because your down payment counted as your initial payment.
- CCSS 5.NBT.7 Add, subtract, multiply, and divide decimals to hundredths, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method and explain the reasoning used.
- CCSS 8.EE.8c Solve real-world and mathematical problems leading to two linear equations in two variables. For example, given coordinates for two pairs of points, determine whether the line through the first pair of points intersects the line through the second pair.
- CCSS A-CED.3 Represent constraints by equations or inequalities, and by systems of equations and/or inequalities, and interpret solutions as viable or nonviable options in a modeling context. For example, represent inequalities describing nutritional and cost constraints on combinations of different foods.
- CCSS A-REI.11 Explain why the x-coordinates of the points where the graphs of the equations y = f(x) and y = g(x) intersect are the solutions of the equation f(x) = g(x); find the solutions approximately, e.g., using technology to graph the functions, make tables of values, or find successive approximations. Include cases where f(x) and/or g(x) are linear, polynomial, rational, absolute value, exponential, and logarithmic functions.
- CCSS F-BF.1 Write a function that describes a relationship between two quantities.
- CCSS F-IF.4 For a function that models a relationship between two quantities, interpret key features of graphs and tables in terms of the quantities, and sketch graphs showing key features given a verbal description of the relationship. Key features include: intercepts; intervals where the function is increasing, decreasing, positive, or negative; relative maximums and minimums; symmetries; end behavior; and periodicity.
- CCSS F-IF.5 Relate the domain of a function to its graph and, where applicable, to the quantitative relationship it describes. For example, if the function h(n) gives the number of person-hours it takes to assemble n engines in a factory, then the positive integers would be an appropriate domain for the function.
- CCSS F-IF.6 Calculate and interpret the average rate of change of a function (presented symbolically or as a table) over a specified interval. Estimate the rate of change from a graph.
- Disneyland
- Universal Studios – Hollywood
- Universal Studios – Orlando
- Desmos online graphing calculator



2 Comments