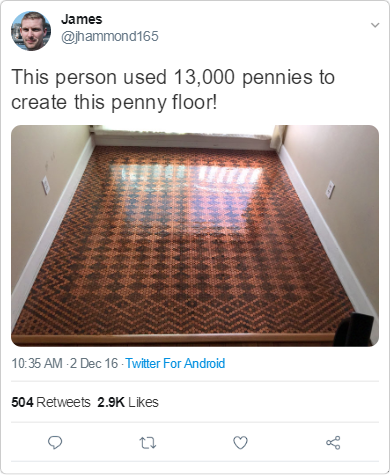
A homeowner tiled her floor with pennies to make the beautiful design seen below.

- How much were those pennies?
These questions may be useful in helping students down the problem solving path:
- What’s a guess that is too low?
- What’s a guess that is too high?
- What’s your best guess?
This beautiful penny-tiled floor was created using approximately 13,000 pennies. That information is provided to us by the homeowner and the actual dimensions needed to calculate the total number of pennies are not provided. So, while at first glance this may appear to be a problem about area, the real focus is on determining how much the value of 13,000 pennies is.
There are multiple ways to approach this problem including multiplying 13,000 pennies x $0.01 per penny for a total of $130. Another way would be to set up a proportion where ($x / 13,000 pennies) = ($0.01 / 1 penny).
Where this problem gets interesting though is what happened when people posted about it on Twitter. Someone initially shared the story and people loved it…
However some people reached a different conclusion about whether it was worthwhile because of how much they believed it cost (“smh” means “shake my head”)…
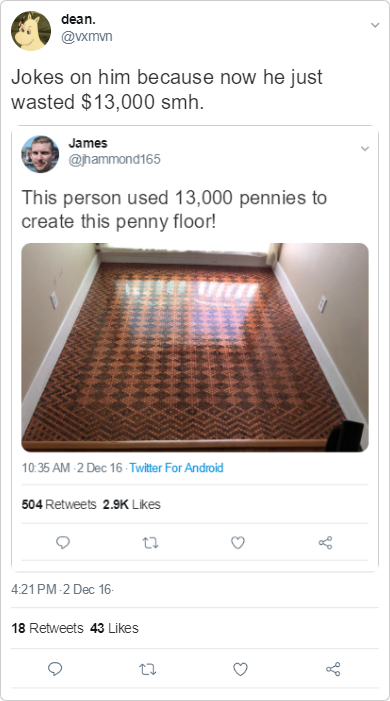
This person (and several others) calculated the pennies’ value to be $13,000 instead of $130, resulting in comical blog posts being written up. This tweet provides us with a great way to challenge students’ ability to articulate their reasoning and intellectual autonomy. I suggest that when you first show students the “correct answer”, you show them the wrong answer where it was calculated to be $13,000.
Try your best to keep a straight face and see what happens. Are they dying to explain why they are right and he is wrong? Or, even worse, do they stop believing in themselves and think he is actually correct? Either way, it should give students an opportunity to implement Math Practice 3 where they need to construct a viable argument and critique the reasoning of others. It also gives you the opportunity to have a conversation about the importance in believing in yourself and being able to articulate your reasoning.
Ultimately, you can end with the tweet below where someone asks Twitter to “never change” because it provides her with such good laughs.
- CCSS 4.MD.2 – Use the four operations to solve word problems involving distances, intervals of time, liquid volumes, masses of objects, and money, including problems involving simple fractions or decimals, and problems that require expressing measurements given in a larger unit in terms of a smaller unit. Represent measurement quantities using diagrams such as number line diagrams that feature a measurement scale.
-
CCSS 5.NBT.5 – Fluently multiply multi-digit whole numbers using the standard algorithm.
-
CCSS 5.NBT.7 – Add, subtract, multiply, and divide decimals to hundredths, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method and explain the reasoning used.
- CCSS 7.RP.3 – Use proportional relationships to solve multistep ratio and percent problems. Examples: simple interest, tax, markups and markdowns, gratuities and commissions, fees, percent increase and decrease, percent error.
- Tonya Tooners via Buzzfeed via April Pforts



Nice problem. Thanks. Several questions might be generated from the photos. How many pennies are needed given the first photo or dimensions in the room? Would that save money over other types of flooring?
I might hesitate using the last tweet and be careful about how I frame the second tweet. The math classroom needs to be a safe place to make mistakes. It may not be a long leap from laughing about an error on twitter to laughing at an error in the classroom or at least the perception that a mistake might cause laughing. We need students to take risks and be open about misconceptions and learning from them.
Thanks Paul. Those are both nice extensions and they take the problem into other standards too. Let me know how it goes in regards to mindset mistakes. Early feedback I’ve received has been positive with no issues regarding safety. Thanks for bringing that to my attention though.
Working on place value with my fifth graders so thought I’d share this with them today. They are in the concrete stage, very concrete, so I wasn’t looking for accuracy just stamina and interest on their part. My favorite quote of the day came after I shared the $13,000 comment. “What? How could they think a penny is worth a dollar? Don’t they know how to do this stuff?” Thank you, Mr. Kaplinsky, for all you do for education!
Thank you so much for sharing this. I’m glad it led to this worthwhile student reflection.
Great real context problem and misconceptions folks have about money/decimals/fractions/conversion/ that show how math and life interact daily in our lives.
Thanks Tricia.
13000 pennies? hmm… I see only about $64 worth of pennies!! here is a slightly different take on the problem:
– Note that the rows and columns across the length and breadth of the floor are constant; that is, any two columns of pennies have the same number of pennies, as do any two rows.
– each bright and dark diamond of the center pattern is made from 16 pennies, four pennies from bottom point to top point and four from left point to right point
– there are 22 dark diamonds going back (length), and 12 dark diamonds going across (width)
– on the sides, there are only five pennies which are added from each point of a dark diamond to get to the wall
– the far and near ends are a problem; where the pattern meets the wall at the front of the picture is obscured; the back is so far back, it’s hard to see the individual rows; i count 11 pennies from the point of any dark diamond to the far wall. maybe 12? maybe 10?
From the above, we can calculate exactly the length and width of the room in pennies:
– width (from side to side) = 5 cents + (12 * 4 cents) + 5 cents = 58 cents
– length (from front to back) = 11 cents + (22 * 4 cents) + 11 cents = 110 cents
Or, total number of pennies in the room = 53 * 110 = 6380, or $63.80
The width of the room is directly observable; this number is correct. As I mentioned, i’m not sure about the number of pennies at the border of the front and back of the room, so we could be off by 100 pennies, plus or minus. Still a far cry from 13,000 pennies!
We’ve made two assumptions here:
a) the pennies are most efficiently packed
b) the room is perfectly rectangular
As an aside, a careful measurement of a sixteen penny diamond shows that pennies directly on top of one another (top of the diamond to the bottom) are 7.5 cm long, and when they are staggered (from one side of the diamond to the other) are 11.7 cm long. The difference is due to the way round objects pack.
So, the dimensions of the room are:
58 cents * 11.7 cm by 110 cents * 11.7 cm, or
678.6cm by 825vm, or
about 22 ft by 27 ft
Thank you for taking the time to share this in such detail along with all your assumptions. I had been focusing on whether the conversion from pennies to dollars was correct, but you could be totally right in that the original quantity of pennies is also not correct. Very interesting.
This problem intrigued me, so I tried to find how many pennies in a square foot if the rows are staggered. This website https://www.real-penny-tile-projects-made-easy.com/how-many-pennies-can-fit-in-one-square-foot-1-sf.html shows at least 288 pennies per square foot. If we assume 13,000 pennies were used in construction of the floor, the size of the room would be 13000/288 is a little more than 45 square feet. This seems reasonable given the one wall has a window that could be about 5-6 feet wide. Fun stuff to have the kids use some pennies and cardboard to try and figure out the room dimensions! Some other photos show a clearer picture of the dormer window area this project decorated. Thanks for finding these gems!
That’s a very reasonable way to approach the problem Karen. You may like David’s approach to it above as a comparison.
Getting ready to start this lesson as a summer school project. I have 5th and 6th graders, so I think we can hit a lot of their math objectives. I am also planning on having them tile the top of a small table with pennies. I will let them figure how many needed, etc… using the dimensions of the table. Hoping this will be a fun summer project at the end of the lesson. Thanks for sharing!
Awesome. Hope it went well JoDee and thanks for sharing your modification.
Thank you so much for this great lesson! I did this today with one my remediation classes today and they loved it. They even wanted to discuss how much it would have been with other denominations. I am working on getting some pennies so I can do a hands-on activity in my classroom with this concept.
This is great to read, Megan. Thanks for letting me know.