How Do Skytypers Write Messages?

• How do skytypers write messages?

These questions may be useful in helping students down the problem solving path:

• Would this message look different to you if you were viewing it from a plane above the message instead of on the ground?

As the video explains, skytyping is a type of skywriting that uses a formation of five planes to create a message in a manner much like old dot matrix printers.  This lesson uses that context as an application for all four transformations: reflections, translations,  rotations, and dilations and their implementation using algebraic notation.  Students begin by using the context of skytyping to create a message and translate it into a set of coordinates.  Then through a series of pretend problems that need correcting, they will need to:

• reflect the message as it was (most likely) written from the wrong perspective
• rotate the message as it was facing the wrong direction
• dilate the message as it needs to be bigger
• translate the message as it was going to be written in the wrong part of the city

After showing students the video to establish the skytyping context, explain that they have been hired to program the planes’ computers to skytype a short message.  Their specific job is to provide the coordinates that the computer will use to make the message.  I am using the word MATH as my message and it will align to my examples.  Other messages will be fine though messages with more characters will have more points to transform.

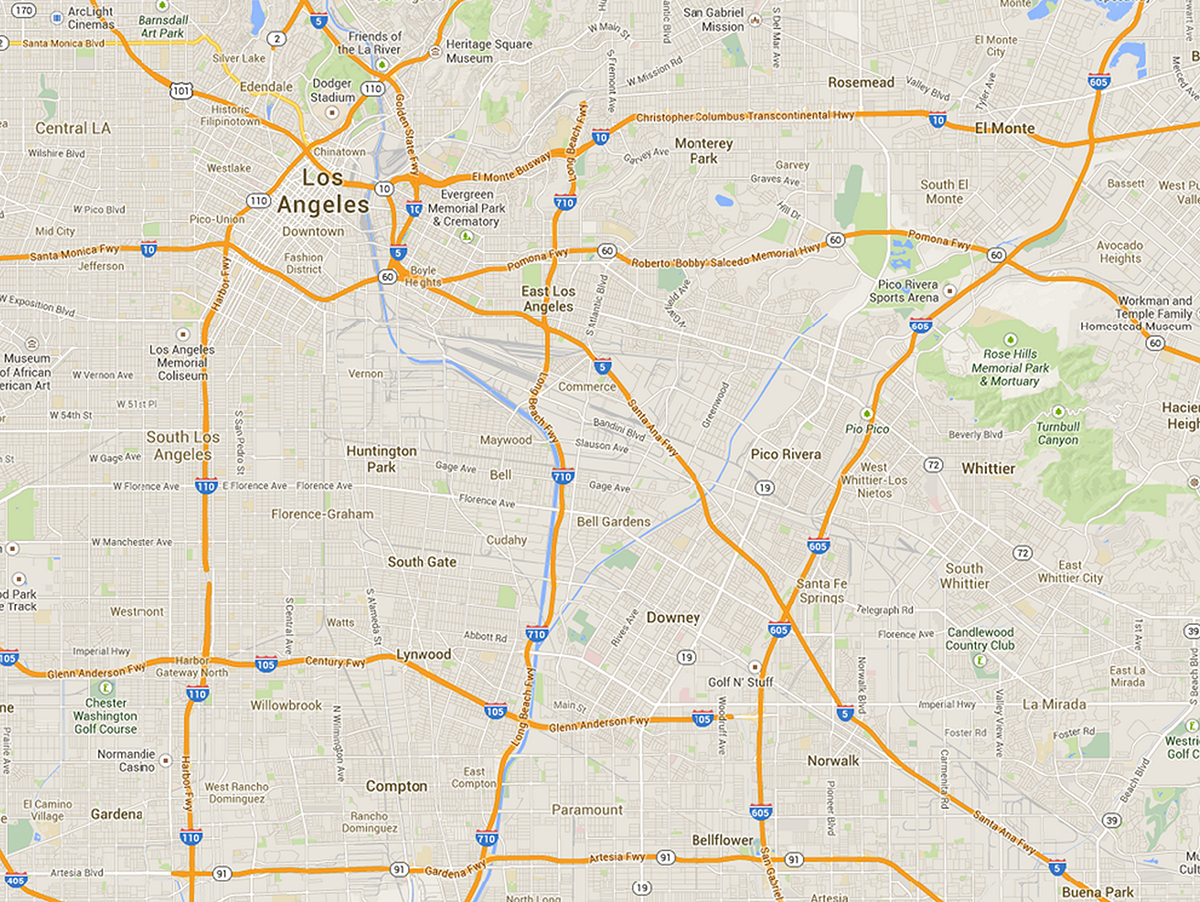
I have provided a map of Los Angeles below to use as the area we will write the message.  It intentionally has no coordinate plane overlaid on top of it.  Ask students, “How can we clearly communicate to the pilots where the message should go?”  Students may say that we can use GPS or where the city or buildings are.  At a minimum, we want them to realize that we need to have a precise way of articulating the message location (Math Practice 6), otherwise the message may not come out looking as we intended.

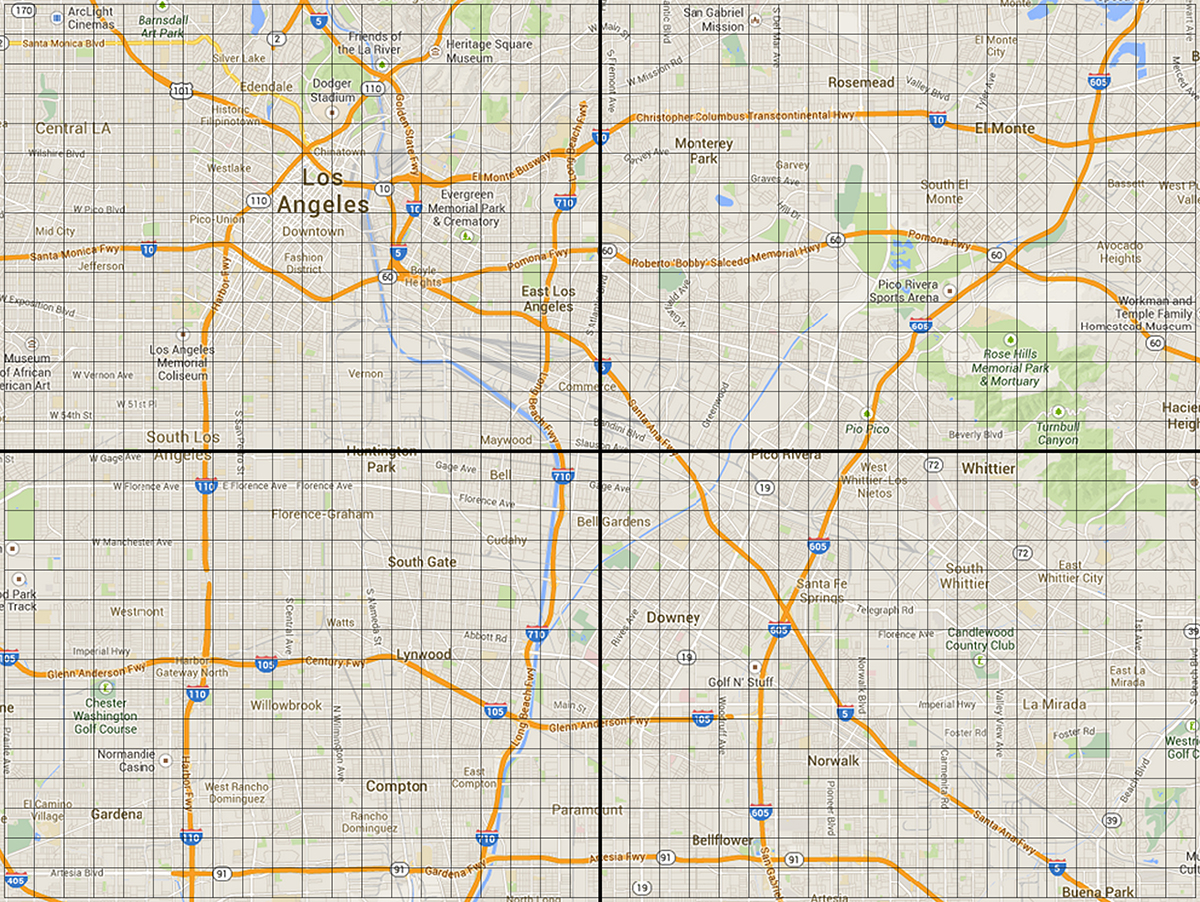
Once they realize this need for precision, present them with the version of the map below that is overlayed with a coordinate plane.

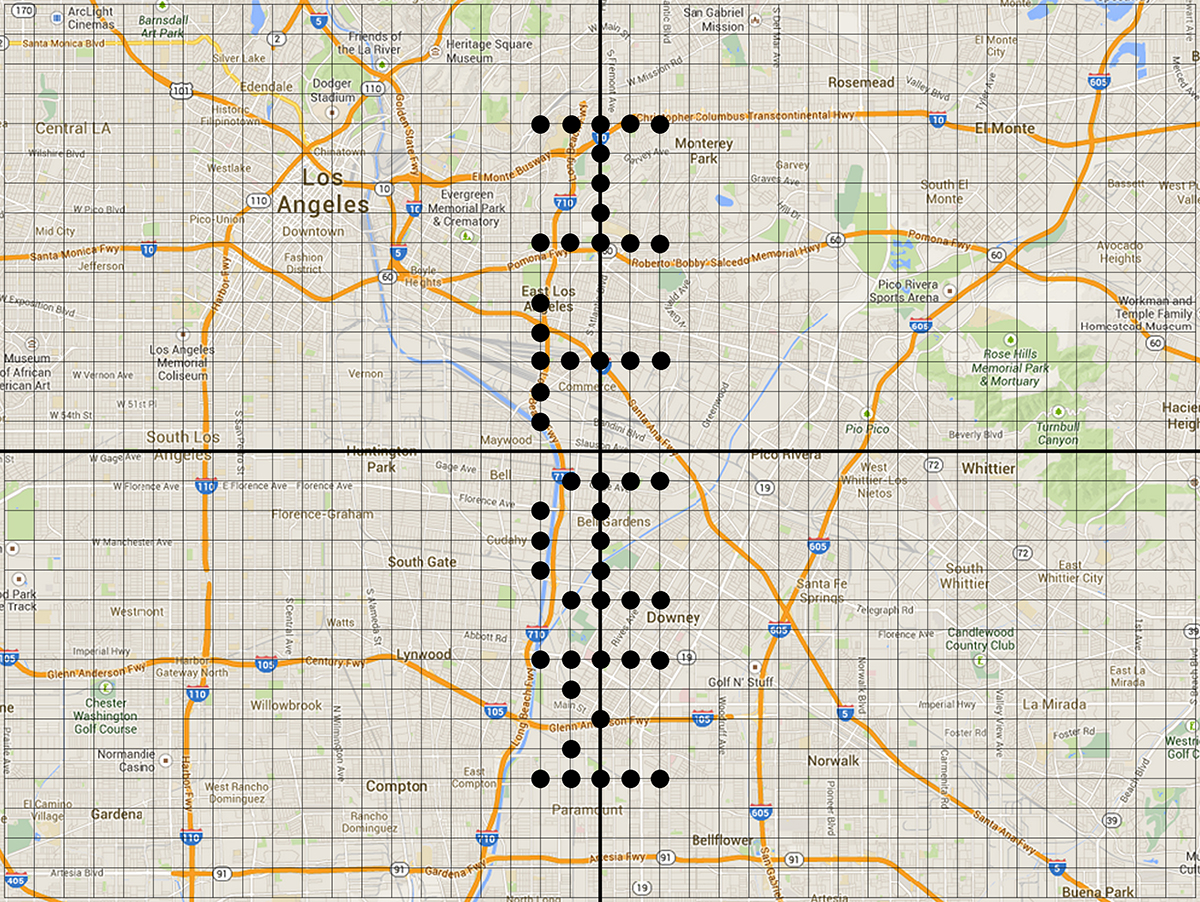
The next goal would be to figure out the message and record it on the map.  Having all students use the same message will make discussions easier as they will have similar results to compare.  Note that I’ve begun by writing the word MATH so that it appears vertically, facing the east.  This is intentional as later it will be rotated 90º clockwise and then dilated.  If it is not horizontal when it’s dilated, it may be too big to fit on the map.

Once students have written their message on the map, have them create a separate list of points for each letter.  My list of points is:

M: {(2, -11), (1, -11), (0, -11), (-1, -11), (-2, -11), (-1, -10), (0, -9), (-1, -8), (-2,-7), (-1, -7), (0,-7), (1,-7), (2, -7)}

A: {(2, -5), (1, -5), (0, -5), (-1, -5), (-2, -4), (-2, -3), (-2, -2), (-1, -1), (0,-1), (1, -1), (2,-1), (0,-2), (0, -3), (0, -4)}

T: {(-2, 1), (-2, 2), (-2, 3), (-2, 4), (-2, 5), (-1, 3), (0, 3), (1, 3), (2, 3)}

H: {(-2, 7), (-1, 7), (0, 7), (1, 7), (2, 7), (0, 8), (0, 9), (0, 10), (-2, 11), (-1, 11), (0, 11), (1, 11), (2, 11)}

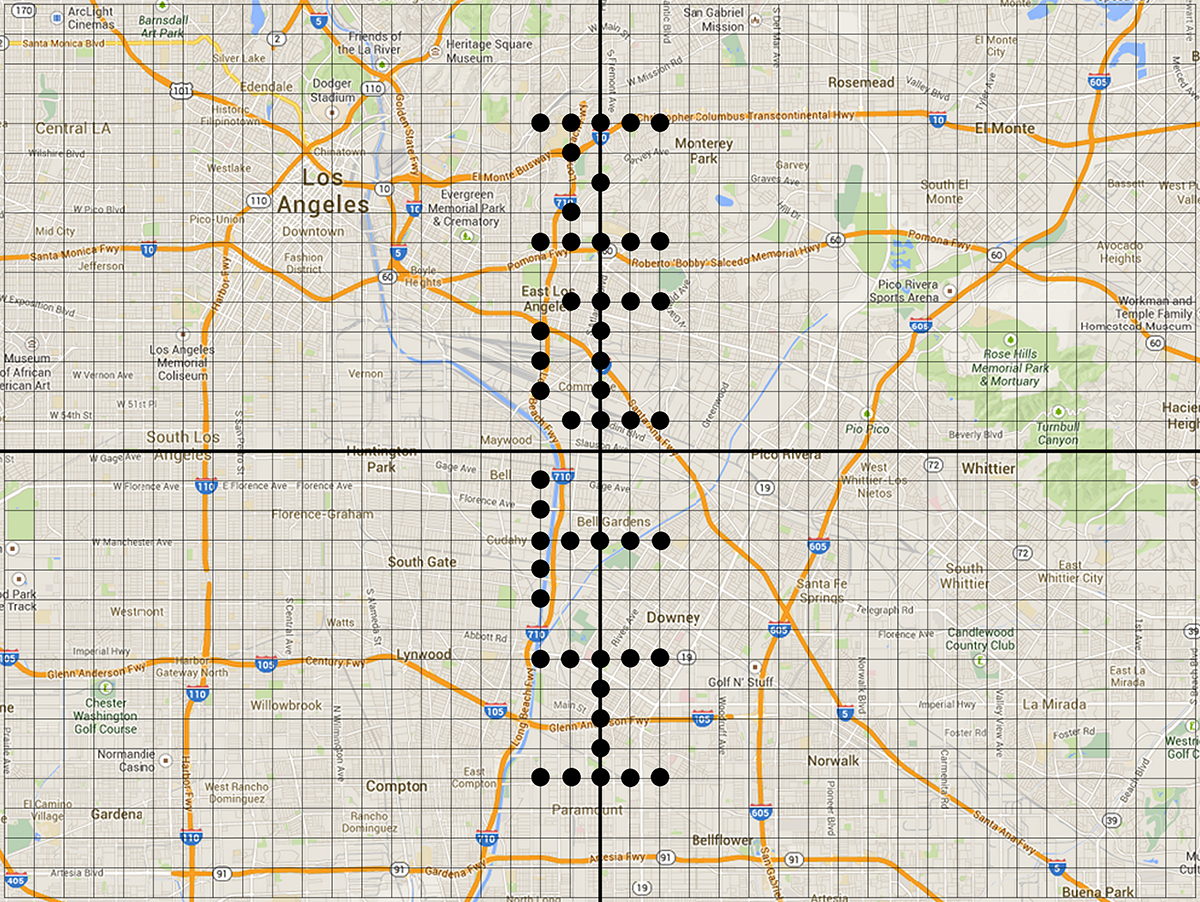
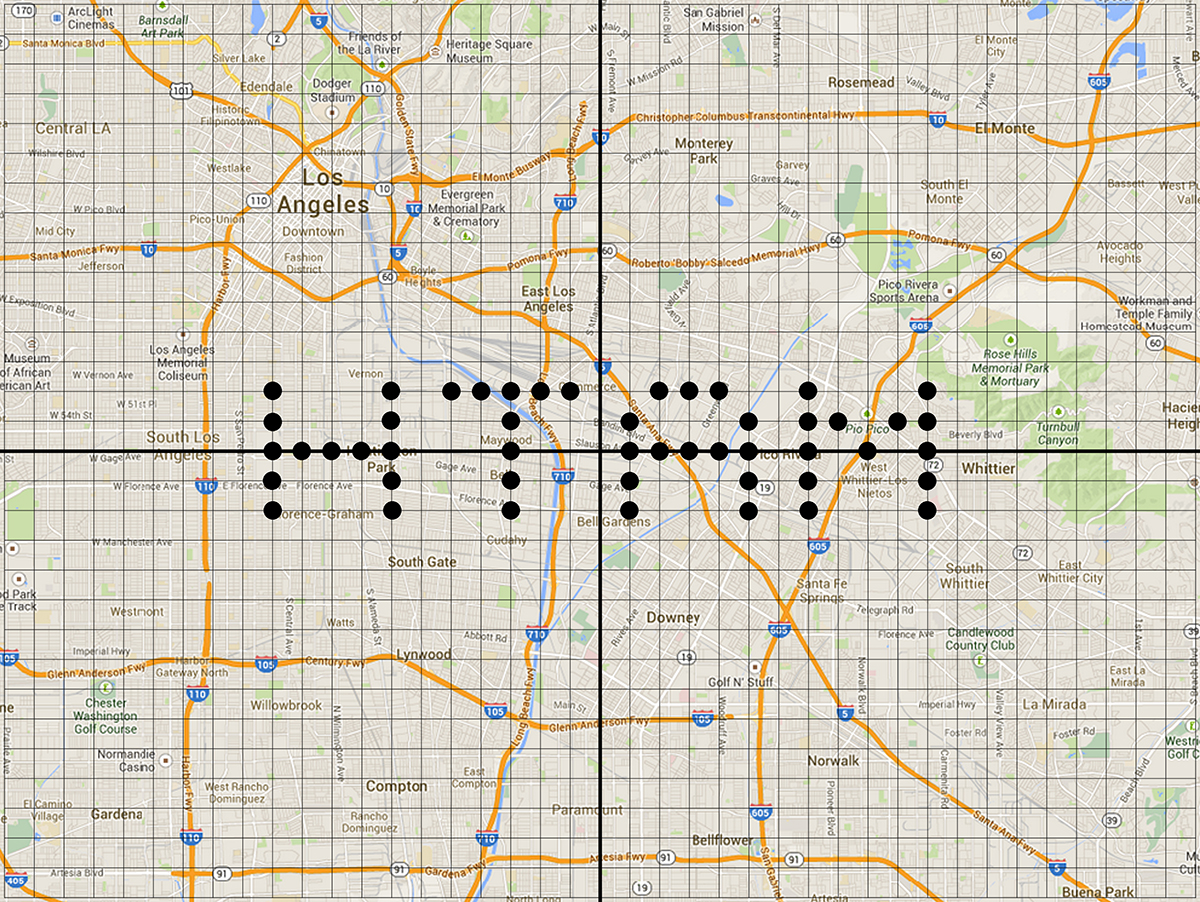
We want the process of recording the points to take some time so that they realize they will want more efficient methods going forward.  There is an intentional mistake that I have made at this point that I hope students will not initially realize.  The mistake is that we have written the message from the perspective of someone reading it from above.  Someone on the ground will see the message backwards.  Try to get students to be the ones to notice this.  Ask them, “Would this message look different to you if you were viewing it from a plane above the message instead of on the ground?”  We want them to realize that they would see the mirror image, or a reflection, of the message we actually desire viewers to see and that the coordinates we previously came up with will no longer work.

The question should then turn to what options we have for figuring out the new coordinates.  Options include:

• Drawing the message over and re-recording the points again by hand
• Figuring a way to re-program the computer using algebra to make this change.

We want students to notice that a reflection across the x-axis means that all of the x-coordinates stay the same but that the y-coordinates switch signs.  Algebraically that is represented by (x, y) → (x, -y).  So if we program the computer to swap the signs of all the y-coordinates, we can fix the problem with the least amount of work.  To help students realize this shortcut, they may need to begin by using option 1 and drawing the message over and re-recording the points again by hand.  We want them to realize shortly into the process that there is a pattern emerging.  Alternatively, if you have access to technology, have students go to http://tinyurl.com/st-stepuno to use Desmos to interactively discover what will create a reflection.  The points are listed in the form (a * b * x + c, a * b * y + c) where it is essentially the point (x, y) with sliders that alter the points to make transformations.  Ultimately you want the results to look like the image below.

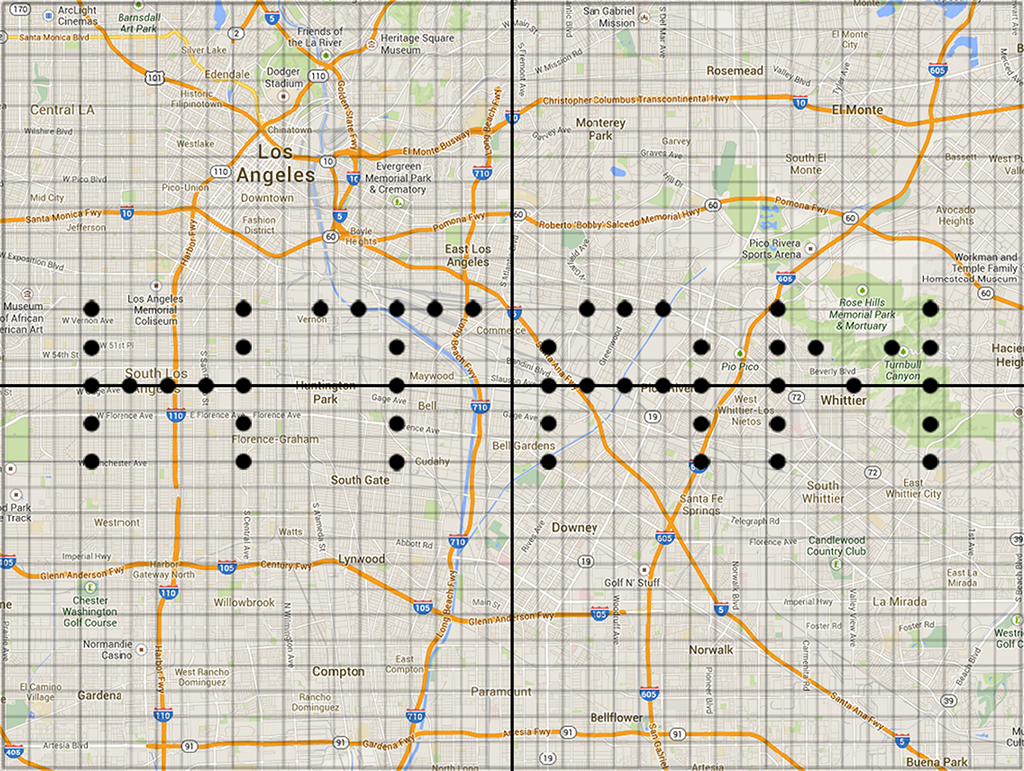
Now with the image properly reflected, the first “problem” comes in.  It turns out that the message was supposed to be read horizontally from east to west instead of vertically from north to south.  Have students figure out that a clockwise rotation of 90º is necessary.   The question should again turn to what options we have for figuring out the new coordinates.  Options include:

• Drawing the message over and re-recording the points again by hand
• Figuring a way to re-program the computer using algebra to make this change.

We want students to notice that a rotation of 90º around the origin means that the x- and y-coordinates swap and the y-coordinates switch signs. Algebraically that is represented by (x, y) → (-y, x).  To help students realize this shortcut, they may need to again begin by using option 1 and drawing the message over and re-recording the points again by hand.  We want them to realize shortly into the process that there is a pattern emerging.  I am trying to find a way to do this with Desmos and will add it if I find it.  Ultimately we want the new message to look like the image below.

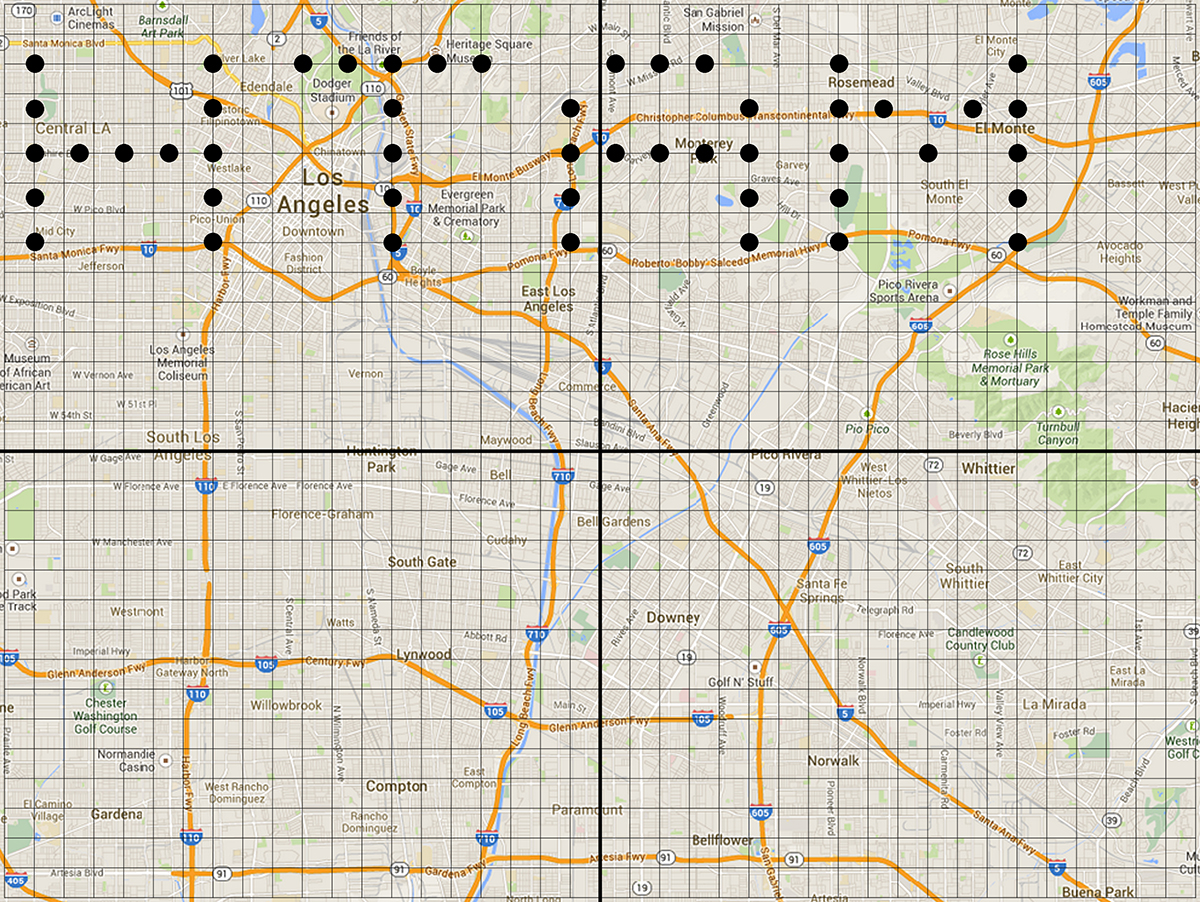
Now the second “problem” comes in.  It turns out that the message is too small to be easily read and needs to be 50% bigger.  The question should again turn to what options we have for figuring out the new coordinates.  Options include:

• Drawing the message over and re-recording the points again by hand
• Figuring a way to re-program the computer using algebra to make this change.

We want students to notice that a dilation by a factor of 1.5 around the origin means that the x- and y-coordinates both get 1.5 times bigger.  Algebraically that is represented by (x, y) → (b*x, b*y) where b = 1.5.  To help students realize this shortcut, they may need to again begin by using option 1 and drawing the message over and re-recording the points again by hand.  We want them to realize shortly into the process that there is a pattern emerging.  Alternatively, if you have access to technology, have students go to http://tinyurl.com/st-step3 to use Desmos to interactively discover what will create a dilation.  The points are listed in the form (a * b * x + c, a * b * y + c) where it is essentially the point (x, y) with sliders that alter the points to make transformations.  Ultimately you want the results to look like the image below.

Now with the image properly sized, the final “problem” comes in.  It turns out that the message was supposed to be closer to Los Angeles in the northwest.  It needs to be move 2.5 units to the west and 10 units to the north.  Have students figure out that the message needs to be moved, or translated towards the new location.   The question should again turn to what options we have for figuring out the new coordinates.  Options include:

• Drawing the message over and re-recording the points again by hand
• Figuring a way to re-program the computer using algebra to make this change.

We want students to notice that each point’s x-coordinate increases by a constant value as does each point’s y-coordinate.  Algebraically that is represented by (x, y) → (x+c, y+d) where c is the change to the x-coordinate and d is the change to the y-coordinate.  To help students realize this shortcut, they may need to again begin by using option 1 and drawing the message over and re-recording the points again by hand.  We want them to realize shortly into the process that there is a pattern emerging.  Alternatively, if you have access to technology, have students go to http://tinyurl.com/st-step4 to use Desmos to interactively discover what will create a translation.  The points are listed in the form (a * b * x + c, a * b * y + c) where it is essentially the point (x, y) with sliders that alter the points to make transformations.  Ultimately you want the results to look like the image below.

• CCSS 8.G.1 Verify experimentally the properties of rotations, reflections, and translations:
• CCSS 8.G.1a Lines are taken to lines, and line segments to line segments of the same length.
• CCSS 8.G.1b Angles are taken to angles of the same measure.
• CCSS 8.G.1c Parallel lines are taken to parallel lines.
• CCSS 8.G.2 Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them.
• CCSS 8.G.3 Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates.
• CCSS 8.G.4 Understand that a two-dimensional figure is similar to another if the second can be obtained from the first by a sequence of rotations, reflections, translations, and dilations; given two similar two-dimensional figures, describe a sequence that exhibits the similarity between them.
• CCSS G-CO.2 Represent transformations in the plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not (e.g., translation versus horizontal stretch).
• CCSS G-CO.3 Given a rectangle, parallelogram, trapezoid, or regular polygon, describe the rotations and reflections that carry it onto itself.
• CCSS G-CO.5 Given a geometric figure and a rotation, reflection, or translation, draw the transformed figure using, e.g., graph paper, tracing paper, or geometry software. Specify a sequence of transformations that will carry a given figure onto another.
• CCSS G-CO.6 Use geometric descriptions of rigid motions to transform figures and to predict the effect of a given rigid motion on a given figure; given two figures, use the definition of congruence in terms of rigid motions to decide if they are congruent.
• CCSS G-SRT.1 Verify experimentally the properties of dilations given by a center and a scale factor:
• CCSS G-SRT.1a A dilation takes a line not passing through the center of the dilation to a parallel line, and leaves a line passing through the center unchanged.
• CCSS G-SRT.1b The dilation of a line segment is longer or shorter in the ratio given by the scale factor.

• Skytypers
• Google Maps
• Desmos