A freeway sign is missing the distances to the upcoming exits.
- What distances should the freeway sign display?
These questions may be useful in helping students down the problem solving path:
- What units do freeway signs usually use to measure distances in the United States?
- What types of numbers are usually written on freeway signs?
- What fraction denominators are options to use?
- How can we determine why our distances are different than the ones on the freeway sign?
- What are possible explanations for the differences?
This lesson is designed to get students arguing about mathematics by using a rich context. The basic premise is that students will compare the freeway sign to the corresponding map to determine the distances that should be listed. Many assumptions will need to be discussed as these non-driving students may not have enough experience to know that:
- distances are listed in miles
- distances are listed as fractions, whole numbers, or mixed numbers
- fractions are only listed as fourths, thirds, or halves
Other issues that are guaranteed to come up during the lesson include:
- how to correctly use a ruler
- how to choose which units to use on a ruler
- how to deal with the issues that come from measuring using decimals (cm) or mixed numbers (inches)
- how to correctly read and use a map including the scale
Also, students may find it useful to make a fraction number line that lists all the possible fractions (and their decimal equivalents) on a freeway sign including 0, 1/4, 1/3, 1/2, 2/3, 3/4, 1, 1 1/4, 1 1/3, 1 1/2, etc. so that students can have a tool to help determine which fraction is closest to the value they came up with. Look out for students who extend their number line towards the negatives. Since distance cannot be negative, the values should all be positive. Perhaps we should call it a number ray.
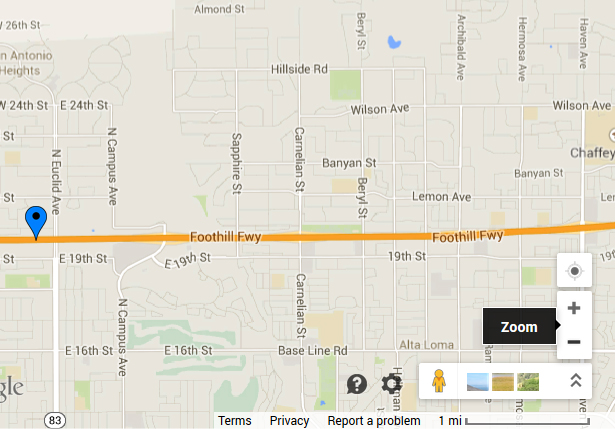
This map involves a reasonably horizontal freeway with perpendicular streets running across it from north to south. Note that Campus Ave has a very peculiar path and appears to go around something as it approaches the freeway. The other two streets, Carnelian St and Archibald Ave are straighter on this map. The scale to show the length of 1 mile is on the bottom right of the map picture.
Using the two images above, I chose to use centimeters and measured one mile to be 3 cm. I measured the distances from the sign as follows:
- Campus Ave – 3.1 cm
- Carnelian St – 6.4 cm
- Archibald Ave – 10.3 cm
Since every 3 cm is one mile, then:
- Campus Ave – 3.1 cm / 3 cm ≈ 1.03 miles
- Carnelian St – 6.4 cm / 3 cm ≈ 2.13 miles
- Archibald Ave – 10.3 cm / 3 cm ≈ 3.43 miles
Next we need to convert those distances to mixed numbers with denominators of 2, 3, or 4:
- Campus Ave – 1.03 miles is very close to 1 mile so I chose a distance of 1
- Carnelian St – 2.13 miles is slightly closer to 2 1/4 than to 2 so I chose a distance of 2 1/4
- Archibald Ave – 3.43 miles is closer to 3 1/2 than 3 1/3 miles so I chose a distance of 3 1/2
The image below shows the original freeway sign. Interestingly, none of my answers match the sign. I would expect similar results from students. It is now a great opportunity to use Math Practice 3 and “construct [a] viable argument and critique the reasoning of others.” A lively conversation should ensue. Honestly, I don’t know why my distances are different. I reason that it could be a combination of:
- the sign has the wrong measurements on it
- my measurements are wrong
- the sign distances were rounded up / down
- I made a calculating error
At the very least, have students defend their answers and state why the sign should be changed. Students could also debate each other if they have different distances.
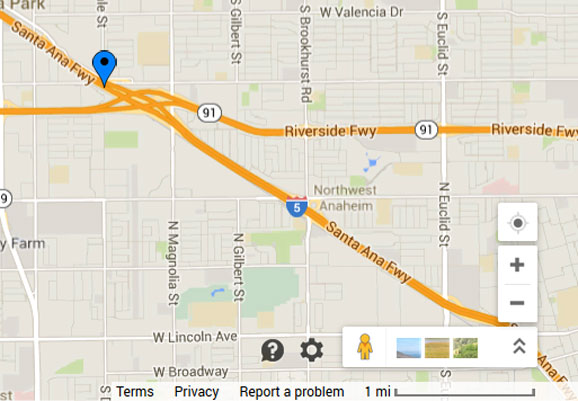
This map has a freeway running diagonally from the northwest to southeast. The other freeway (Riverside Fwy 91) that runs from east to west is not the freeway we are using. Note that there are four streets (Magnolia St, Brookhurst St, La Palma Ave, and Euclid St) and only three distances on the freeway sign. That is because Brookhurst St and La Palma Ave have the same distance listed. Every street except La Palma Ave runs from north to south. La Palma Ave is not labeled on the map but it runs from east to west and intersects Brookhusrt St perpendicularly where the “5” is located. The scale to show the length of 1 mile is on the bottom right of the map picture.
Using the two images above, I chose to use centimeters and measured one mile to be 3.6 cm. I measured the distances from the sign as follows:
- Magnolia St – 2.1 cm
- Brookhurst Rd / La Palma Ave – 6.4 cm
- Euclid St – 10.1 cm
Since every 3.6 cm is one mile, then:
- Magnolia St – 3.1 cm / 3.6 cm ≈ 0.58 miles
- Brookhurst Rd / La Palma Ave – 6.4 cm / 3.6 cm ≈ 1.78 miles
- Euclid St – 10.3 cm / 3.6 cm ≈ 2.81 miles
Next we need to convert those distances to mixed numbers with denominators of 2, 3, or 4:
- Magnolia St – 0.58 (technically 0.5833333…) miles is right in the middle of 1/2 and 2/3 and I chose a distance of 1/2
- Brookhurst Rd / La Palma Ave – 1.78 miles is very close to 1 3/4 so I chose a distance of 1 3/4
- Euclid St – 3.43 miles is closer to 3 1/2 than 3 1/3 miles so I chose a distance of 3 1/2
The image below shows the original freeway sign. Again, none of my answers match the sign and I would expect similar results from students. It is still a great opportunity to use Math Practice 3 and discuss whether the answers are off because of a combination of:
- the sign has the wrong measurements on it
- my measurements are wrong
- the sign distances were rounded up / down
- I made a calculating error
At the very least, have students defend their answers and state why the sign should be changed. Students could also debate each other if they have different distances.
-
CCSS 3.NF.1 – Understand a fraction 1/b as the quantity formed by 1 part when a whole is partitioned into b equal parts; understand a fraction a/b as the quantity formed by a parts of size 1/b.
-
CCSS 3.NF.2 – Understand a fraction as a number on the number line; represent fractions on a number line diagram.
-
CCSS 3.NF.2a – Represent a fraction 1/b on a number line diagram by defining the interval from 0 to 1 as the whole and partitioning it into b equal parts. Recognize that each part has size 1/b and that the endpoint of the part based at 0 locates the number 1/b on the number line.
-
CCSS 3.NF.2b – Represent a fraction a/b on a number line diagram by marking off a lengths 1/b from 0. Recognize that the resulting interval has size a/b and that its endpoint locates the number a/b on the number line.
-
CCSS 3.NF.3 – Explain equivalence of fractions in special cases, and compare fractions by reasoning about their size.
-
CCSS 3.NF.3a – Understand two fractions as equivalent (equal) if they are the same size, or the same point on a number line.
- CCSS 4.MD.2 – Use the four operations to solve word problems involving distances, intervals of time, liquid volumes, masses of objects, and money, including problems involving simple fractions or decimals, and problems that require expressing measurements given in a larger unit in terms of a smaller unit. Represent measurement quantities using diagrams such as number line diagrams that feature a measurement scale.
- CCSS 5.NBT.7 – Add, subtract, multiply, and divide decimals to hundredths, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method and explain the reasoning used.
- CCSS 6.NS.1 – Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions, e.g., by using visual fraction models and equations to represent the problem. For example, create a story context for (2/3) ÷ (3/4) and use a visual fraction model to show the quotient; use the relationship between multiplication and division to explain that (2/3) ÷ (3/4) = 8/9 because 3/4 of 8/9 is 2/3. (In general, (a/b) ÷ (c/d) = ad/bc.) How much chocolate will each person get if 3 people share 1/2 lb of chocolate equally? How many 3/4-cup servings are in 2/3 of a cup of yogurt? How wide is a rectangular strip of land with length 3/4 mi and area 1/2 square mi?.
- CCSS 7.NS.3 – Solve real-world and mathematical problems involving the four operations with rational numbers.1
- CCSS 7.RP.1 – Compute unit rates associated with ratios of fractions, including ratios of lengths, areas and other quantities measured in like or different units. For example, if a person walks 1/2 mile in each 1/4 hour, compute the unit rate as the complex fraction 1/2/1/4 miles per hour, equivalently 2 miles per hour.







On the first example, I believe your measurements are correct. The reason why it doesn’t match with the freeway sign is because you don’t know the exact place that the freeway sign is. At least, that is what I believe. I took your measurement differences between Carnelian and Archibald and noticed it is 1 and 1/4 of a mile which is the same difference as is on the freeway sign. Just my thoughts.
It’s hard to remember now that it’s been about 3.5 years, but you can find the exact location of the sign on the map and measure from there. It could also be that the street is not perfectly straight. Either way, worth having conversations about sources of error.
I’m thinking that the reason your answers are incorrect is because the freeway signs show how far it is until the EXIT. The signs don’t show how far it is until you get to that particular street. So if you want a more accurate answer, you need to measure from the starting point to where the EXIT ramp is on the map (which means you probably have to zoom in closer to see that).
Ooooh. I’d never considered that. I wonder if there is a way to verify that. I imagine that the difference between the beginning of the exit and the actual street should be fairly small.
The distance listed on the sign is to the beginning of the exit, as suggested above. The distance listed should be about 1/4 mile to 1/2 mile less than the actual distance to the road itself, which seems to fit with your calculations overall.