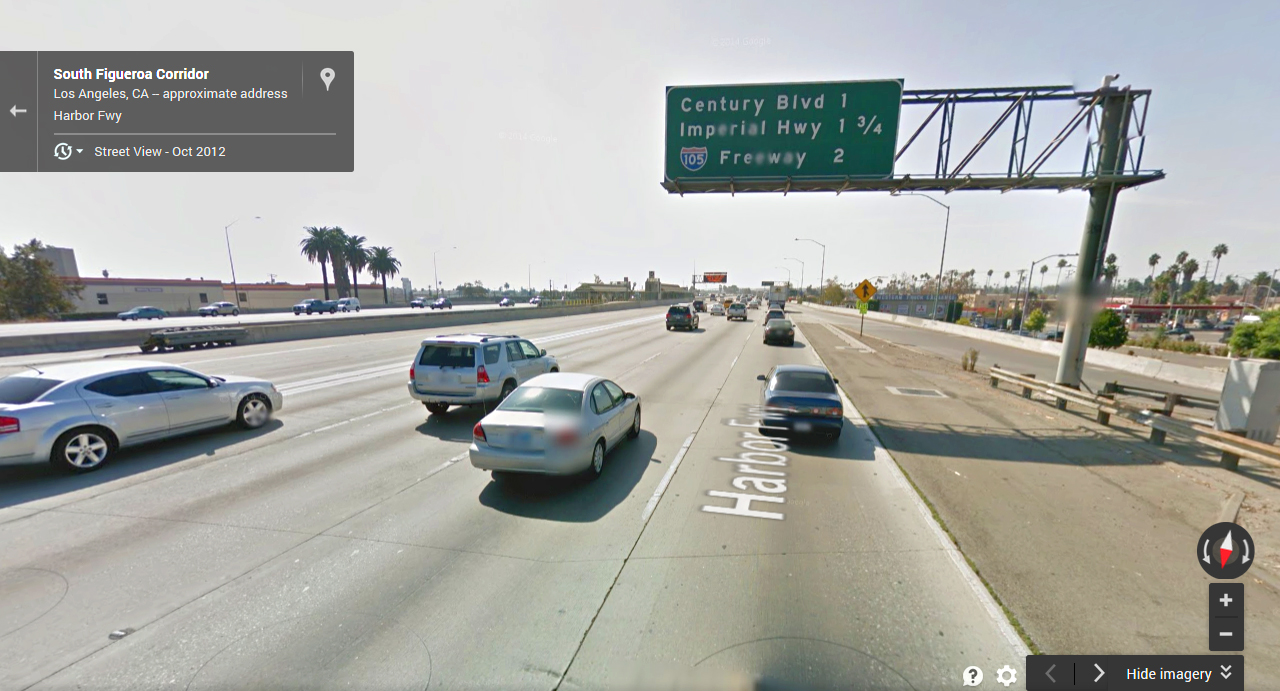
- Where is the freeway sign located?
- How can we figure out what the fractions represent?
- How many exit distances do we need to know to determine the sign’s location?
- How can we use the distances to determine the exit’s location?
- What information do we already know that will be useful to solve the problem?
- What information do we need to know to solve the problem?
The first of the two problems I have provided comes from the 110 freeway in Southern California. Looking at the picture below I want students to focus on the freeway sign which lists the names of the upcoming exits and their distances as fractions of a mile. This would be a good time to ask students “How can we figure out what the fractions represent?” to make sure that they understand the sign’s context.
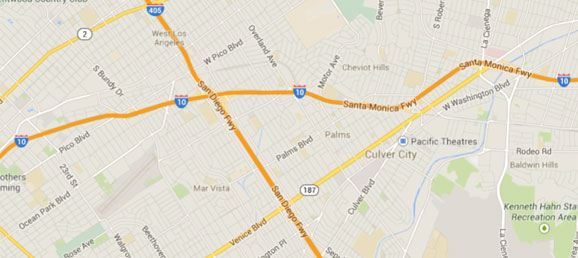
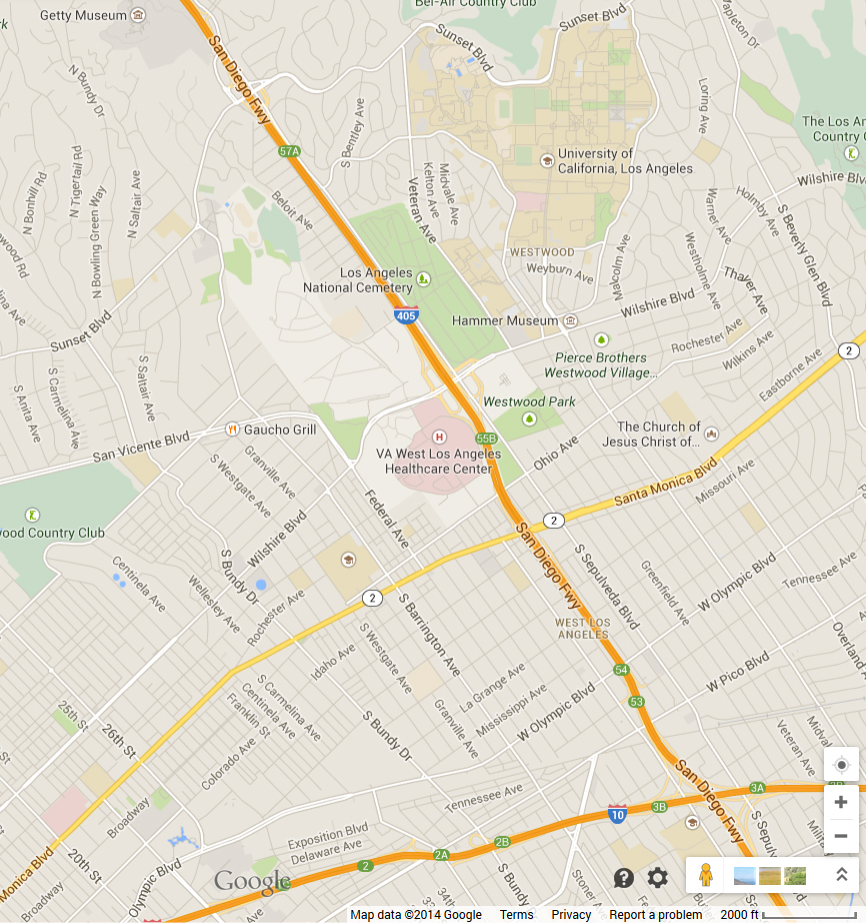
With that completed I would present The Challenge question and ask the students “Where is the freeway sign located?” I can make a case for and against giving students the map at this point versus having them realize that they need a map to precisely identify the location. Once the need for a map is established, provide the image below.
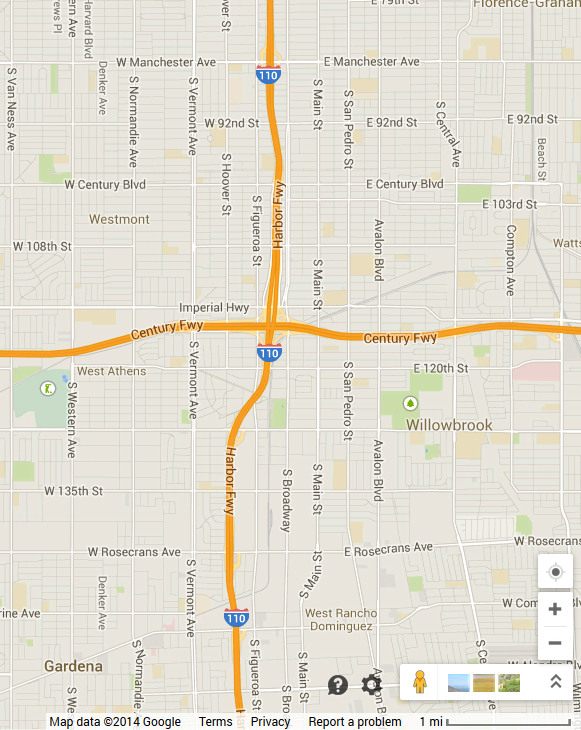
Now that students have this map, ask students, “How can we use the distances to determine the exit’s location?” Expect students to want rulers to complete this activity. Also expect there to be differing answers as to where the correct location should be. It will be a great opportunity to discuss why the answers vary. Reasons could include:
- Calculation errors
- Measurement errors
- The reality that the exits are rarely exactly that fraction away and instead the sign makers round to the nearest fourth of a mile.
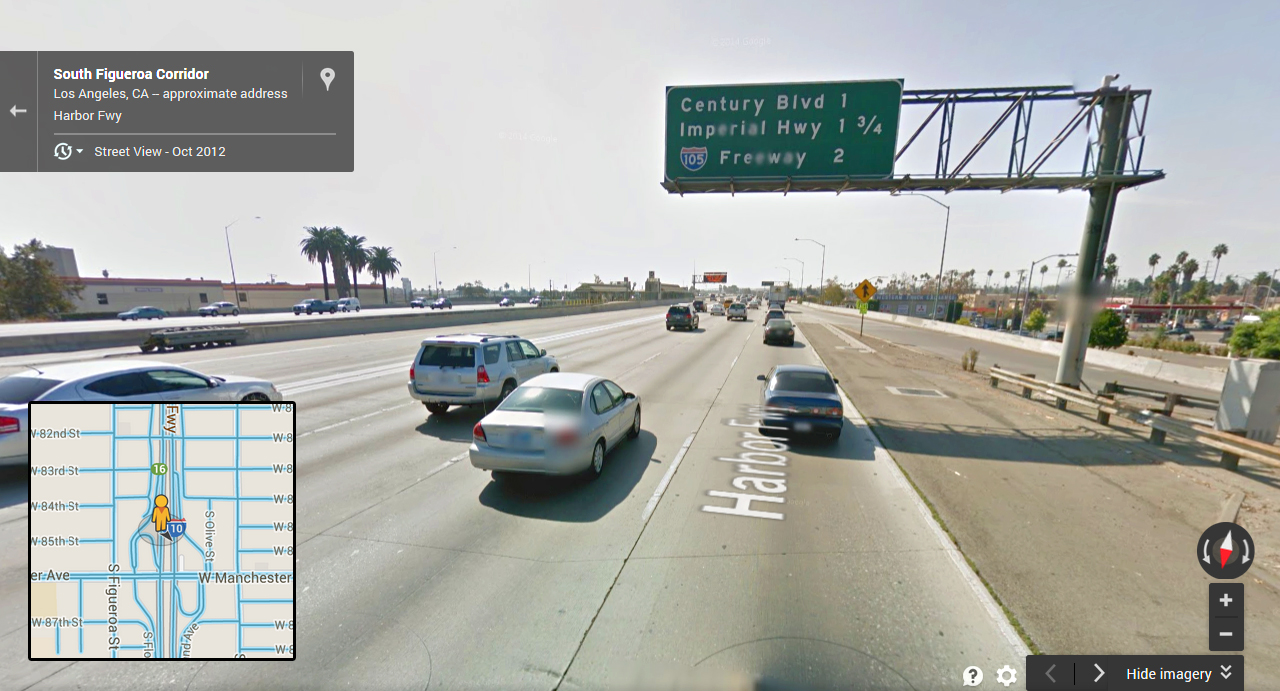
Finally present the actual answer using the image below. Note that it is very similar to the first picture but has a square box in the lower left with a yellow person icon to identify where the image is taken from (and therefore very close to the freeway sign). This particular image was taken just north of Manchester Ave near the top of the map.
- 405 Freeway view without answer

- 405 Overhead map view
- 405 Freeway view with answer

- CCSS 3.NF.1 Understand a fraction 1/b as the quantity formed by 1 part when a whole is partitioned into b equal parts; understand a fraction a/b as the quantity formed by a parts of size 1/b.
- CCSS 3.NF.2 Understand a fraction as a number on the number line; represent fractions on a number line diagram.
- CCSS 3.NF.2a Represent a fraction 1/b on a number line diagram by defining the interval from 0 to 1 as the whole and partitioning it into b equal parts. Recognize that each part has size 1/b and that the endpoint of the part based at 0 locates the number 1/b on the number line.
- CCSS 3.NF.2b Represent a fraction a/b on a number line diagram by marking off a lengths 1/b from 0. Recognize that the resulting interval has size a/b and that its endpoint locates the number a/b on the number line.
- CCSS 3.NF.3 Explain equivalence of fractions in special cases, and compare fractions by reasoning about their size.
- CCSS 3.NF.3a Understand two fractions as equivalent (equal) if they are the same size, or the same point on a number line.
- CCSS 3.NF.3b Recognize and generate simple equivalent fractions, e.g., 1/2 = 2/4, 4/6 = 2/3. Explain why the fractions are equivalent, e.g., by using a visual fraction model.
- CCSS 3.NF.3c Express whole numbers as fractions, and recognize fractions that are equivalent to whole numbers. Examples: Express 3 in the form 3 = 3/1; recognize that 6/1 = 6; locate 4/4 and 1 at the same point of a number line diagram.
- CCSS 3.NF.3d Compare two fractions with the same numerator or the same denominator by reasoning about their size. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with the symbols >, =, or <, and justify the conclusions, e.g., by using a visual fraction model.
- Google Maps – 405 Freeway
- Google Maps – 110 Freeway