Have you ever believed something about your students only to find out that you were not correct? This has happened to me many times and it doesn’t feel good when the reality kicks in that you were wrong. I remember a specific instance of this happening to me as I transitioned from teacher to teacher specialist.
When I was in teaching full time at a middle school, I was very proud of having classes where students began the year with varying proficiency levels but by the end of the year would all score Advanced or Proficient, as measured by the California state assessment.
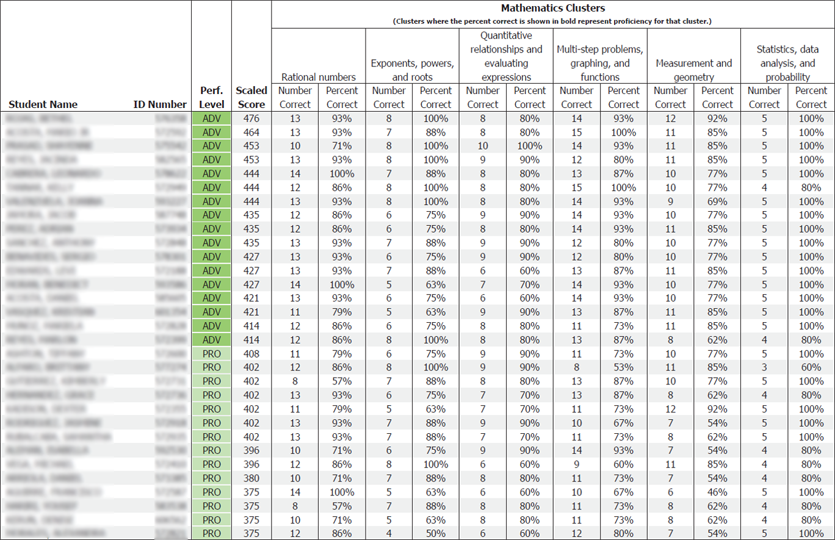
To me it showed that I helped students develop very strong mathematical understandings… or so I thought.
Soon after, I left the classroom and became a teacher specialist in my same district, Downey Unified School District. As part of my new position, I taught lessons at the high school and many of my former middle school students were there. On one particular day, I taught a lesson to students that required content knowledge of slope.
I expected this to be no problem, because many of these students had learned about slope in my class and had scored very well. However, I couldn’t deny the reality that these students had huge gaps in their understanding of slope. Some even said that their teacher never taught it to them, not realizing that I was that teacher!
Let’s just say that it was a rather humbling day. While I didn’t know what exactly had happened, I couldn’t deny that something was wrong. Somehow, the way I taught them slope did not create lasting understanding. I didn’t know how to reconcile the reality that kids could score advanced and proficient on a state standardized test yet still not understand the content.
Over the coming weeks and months, I reflected a lot on what had happened. As hard as it was to stomach, what I came to realize was that I was the problem. I had been focusing on a very superficial level of understanding. I knew that the state assessment would only ask them questions like this one below.
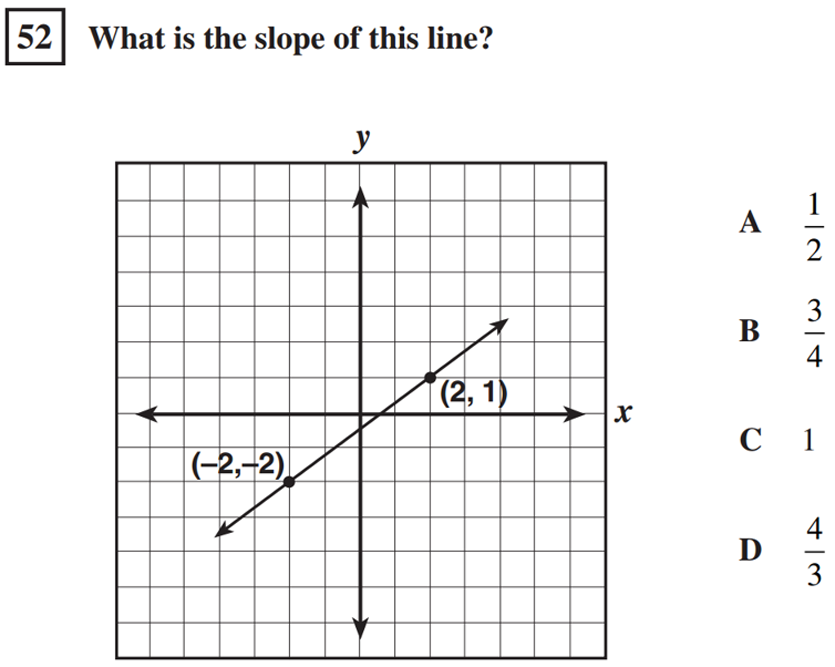
As long as they could count the rise and run or apply the slope formula, they would be able to solve the problem. So, that’s basically all I taught. I spent very little time building deeper conceptual understanding and talking about slope as steepness of a line or rate of change.
It now seems obvious to me that this was a bad idea, but at the time all the data showed that I was doing just fine. I clearly had students with huge gaps in their understanding, but I couldn’t identify who they were. I wished that I had something like X-Ray Vision glasses where I could look into students’ brains and see their misunderstandings.

Instead, all I got were false positive affirmations of their understandings. Put simply, when I asked superficial questions, I got superficial results back. Looking back, if I had some sort of X-Ray Vision glasses that truly measured student understandings, the test results would have looked more like this.
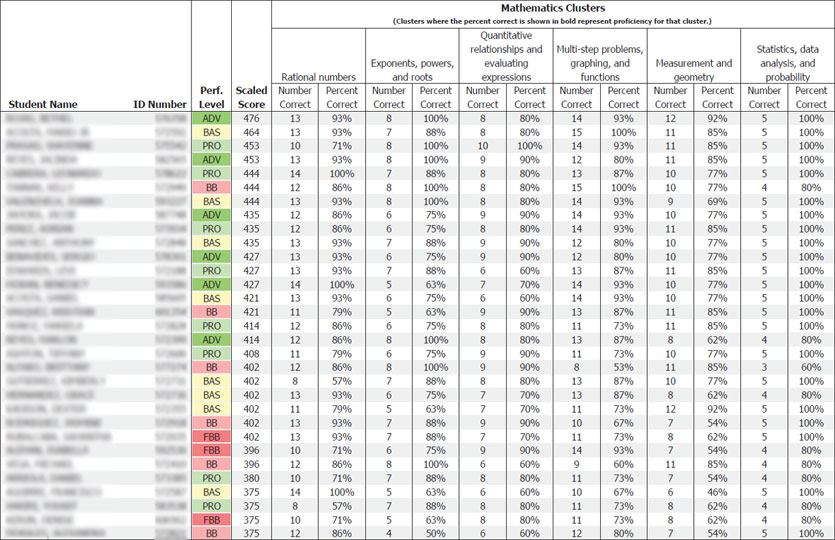
Results like this would have been unacceptable to me, but I wasn’t aware of them. It is more obvious to me now, but using questions like the ones I was using to prepare students for the state test did not give me enough information to truly measure a student’s understanding. This begs the question: “How do you know which kinds of questions will more precisely measure students’ understanding?”
For me, I have come to believe that higher depth of knowledge questions like those on Open Middle are my X-Ray Vision glasses when I want to uncover misunderstandings. What are yours? Let me know in the comments.


I love it when students say that nobody taught that and they are in my class for 4 semesters!
That said, I always look for ways to teach and learn at deeper level of understanding.
I love the X-ray analogy,
Thank you
Ha! Totally Mariève! It can be very humbling, but perhaps all those times they told me that nobody taught them that, what they really were trying to say was “Nobody ever taught me that in a way that made sense and I could remember.” Lots to reflect on.
Ratios and Proportions. You can ask a problem, “Marth is traveling at a constant rate of 60 mph, how long does it take her to travel 180 miles?” I will find that most students will answer that without thinking why they divide, or create cross product.
However I asked a great problem from PD I went to. “You are mixing green paint. You make green paint by mixing 2 parts blue and 3 parts yellow. How many pails of paint of yellow and blue do you need to make 100 pails of paint of green?”
Almost everyone’s first answer is 500 pails of paint. 200 blue and 300 yellow…While they are not wrong, it is a big waste of paint. This problem is really a theme of proportions, ratios and percentages. This concept my students really struggle with…
I find when I ask questions that aren’t so surface level, answers are varied and are a maze of multiplication and division…
Thanks Madeline. We’re definitely on the same page about incorporating problems that get people to think beyond surface level reasoning.
Many students and teachers believe they know poor place value“ if they can name the places to the left and the right of the decimal point.
So my favorite question related to depth of understanding is:
“how much bigger is the 5 at A than the 5 at B?
And assuming that this comment field does not truncate initial spaces, it would look like this:
A B
555.55
I ask my question in a ambiguous fashion on purpose to see if students are thinking additively or multiplicatively. My intention is that the A is in the tens place in the B is in the tenths place. Students who are thinking additively will say 49 1/2 bigger. Students who are thinking multiplicatively will say 100 times bigger. Some of the students who say it is 100 times bigger will have divided 50 by .5 using the long division algorithm. The student who says that each time you have the same digit one place to the left it’s 10 times bigger than the same digit to the right has some understanding that we’re looking for.
Thanks Robert. I appreciate you adding this example to the conversation.
HI Robert,
Great point about deeper thinking. I am a big fan of your open middle problems and am trying to incorporate it into my tutoring sessions.Thanks a bunch for those. I am trying to very hard to incorporate deeper thinking on my part to the students. To the point of understanding slope, I feel that school systems (not being judgemental here) overteach slope and underteach the rate of change concept in Algebra 1. The students struggle in the interpretation of slope in word problems. I give them this analogy: ” you dont go to a rental store or a gym and ask them what their slope is. You ask them the hourly rate or daily rate for what you are renting”.
Your contribution to math education is admirable. Hope it can elevate the students’ DOK overall
Early in my career, I would 100% agree with “I feel that school systems (not being judgmental here) over teach slope and underteach the rate of change concept in Algebra 1.” That being said, I feel like the Common Core standards definitely shifted it back to context.
That being said, it will take time and professional development to see how people teach it shift in classrooms.