Every once in a while I’ll work with a teacher who dismisses higher depth of knowledge problems such as those on Open Middle as common brainteasers with limited value. While I understand that Open Middle problems have similarities to brainteasers, I believe that there are significant differences that cannot be overlooked.
Consider the two second grade math problems below:

Source: Puzzles and Problems
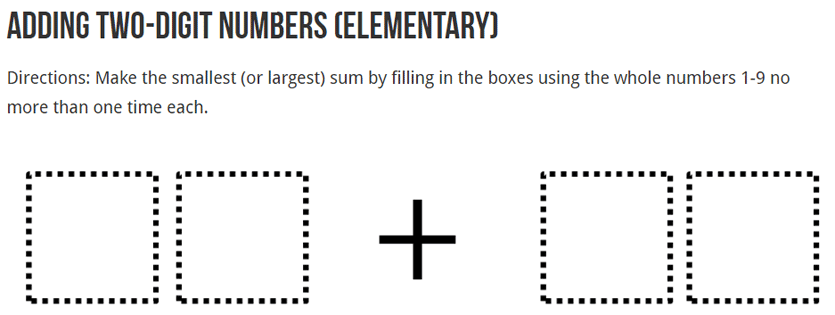
Source: Open Middle
Here’s how I compare them:
- Problem One helps students build problem solving skills but does not connect to any specific math content.
- Problem Two also helps students build problem solving skills, but an important difference is that it is strongly connected to a specific math content standard. Students will build deeper understanding about addition and place value and that did not happen with Problem One.
As such, I see Problem One as a brainteaser that builds problem solving skills and Problem Two as a higher depth of knowledge problem that incorporates specific math content in addition to building problem solving skills.
I asked others what they thought about the differences between Open Middle problems and brainteasers:
Hey @openmiddle fans, do you see open middle problems as the same or different than brainteasers? Why? #openmiddle #probchat #DOK #MTBoS
— Robert Kaplinsky (@robertkaplinsky) May 4, 2015
Here’s what they had to say:
@fawnpnguyen @robertkaplinsky @openmiddle I agree OMP allow for multiple approaches and/or solutions where BT seemed closed most of the time
— Mike Flynn (@MikeFlynn55) May 4, 2015
@robertkaplinsky @openmiddle I think the purpose is the difference. OMP are designed to learn important math. BT are designed to trick!
— Mark Chubb (@MarkChubb3) May 5, 2015
@robertkaplinsky @openmiddle Mostly different. Brainteasers tease (sometimes annoyingly and waste of time). OMP allows more exploration.
— Fawn Nguyen (@fawnpnguyen) May 4, 2015
@robertkaplinsky I like that @openmiddle scaffolds the meta-cog reflective piece, brain teasers don’t necessarily have that embedded.
— Andrew Gael (@bkdidact) May 6, 2015
What’s your take on the difference between brainteasers and Open Middle problems? What do you agree or disagree with? Let me know in the comments.

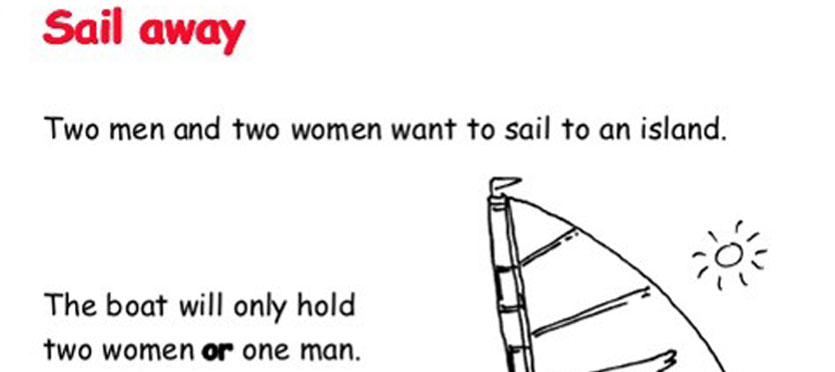
I’m going to use the specific examples you gave, since we all know that there are challenges of both types across the spectrum from bad to great (though I’ve rarely seen a truly terrible open middle problem).
For me, brainteasers like this do fit into my curriculum, but they are used for meta skills:
(1) what tools can we use to helpfully organize our work and information? Drawing a diagram, making a table are both reasonable for this sailboat problem. Acting out the story would also work, esp fun for very young kids.
(2) Identify and confront our instinctive assumptions. Fundamentally, this is what makes something a brain-teaser, I think. We see the problem and make an assumption that blocks us from the answer. For this example, the assumption might be that people only go one way on the sailboat (from shore to the island). For very young kids, this isn’t so much of an issue, they have fewer biases and really delight in wacky interpretations. My 4 year old suggests that the sailboat doesn’t need to be crewed, so there’s no issue at all, just send it back empty. For adults, brainteasers are a more intentional practice in confronting assumptions. I don’t know what age students cross over.
(3) Extensions and generalizations. The mathematician in me sees that puzzle and thinks about generalizations like:
M men and W women want to sail to the island. The boat will hold at most 1 man or 2 women. How can they get to the island? What is the minimum number of trips? How many crossings must the women make? Can the crossings by the women be divided evenly (all women make the same number of crossings)?
There might be other ways of generalizing the constraint. Perhaps a * m + b* w < c where m and w are the number of men and women, resp, in the boat?
I want to encourage the kids to think about extensions themselves. Building interesting questions is itself a hugely valuable skill.
Also, these generalizations and extensions naturally link with standard curricular content as we explore them.
I think OMP share characteristics (1) and (2), though point (2) is usually much weaker since OMP's aren't built around triggering assumptions. For characteristic (3), I often struggle to find a compelling extension/generalization exploration coming from OMP (like this example). That might just be a matter of personal taste, though.
Finally:
(4) People think brainteasers are fun, only math teachers think OMP are fun! I'm joking and exaggerating a bit, but I sense my non-math friends wouldn't get so jazzed about the smallest possible sum. If I had any non-math friends…
This is really interesting Josh. I wonder if the differences you describe should be attributed to Open Middle problems (OMP) as compared to brainteasers (BT) or instead to problems with a context as compared to problems without a context.
For example, while I can’t think of one right now, I imagine that there is a BT out there without a context that would not hold up well to your 2nd point. I think the same for your 3rd point in that having a context helps you think about where else it could go.
Regarding your 4th point, I might actually push back on you the most there. Based on years of scientific research I have conducted (and by that I mean looking on Facebook), I have seen some ridiculous traction from problems that are just asking people to apply the order of operations and say what answer they got. I guess those are not really OMP or BT but I think that people are more likely to engage in BT because of the context.
What do you think? Am I oversimplifying it by making it a context / no context distinction?
Interesting, I never really thought of OMP as being brain teasers, but I can see why people made that connection.
I feel like OMP are more content based like you said, but I don’t think of all brain teasers as puzzles with tricks. Maybe these aren’t brain teasers, but I’m thinking of Ted-Ed Riddles (http://blog.ed.ted.com/2016/02/02/can-you-solve-these-5-ted-ed-riddles/) which I use all the time in class. I think these are great for utilizing many of the math practices without their focusing on an underlying standard.
Both OMP and BT often utilize guess and check. The major difference being OMP always result in an answer with the students feeling some sort of accomplishment. Even if they didn’t find the “smallest value” or whatever the prompt is, they completed something. Brain teasers don’t give you that feeling if you don’t find the answer right away. That’s why I think BT are usually more frustrating than OMP.
Even though BT can be more frustrating than OMP, I will admit that my students typically enjoy them (BT) more. My guess is because they typically have some sort of story involved and they are out of the ordinary…which I think is what you were getting at with the “context vs no context” problems. Plus that “aha” moment when (or if) they finally figure out the riddle is really exciting!
Ultimately, I don’t think they’re the same. They have a similar feel with some distinct differences.
Don’t forget the fluency practice students are getting with OMP and the number sense that is being built as they try to determine the greatest or smallest number.
Totally Julie. I think there are a lot of benefits to Open Middle problems.
Limits. OMPs often include a process of finding the limits within a set of constraints which is a logical and mathematical process which requires understanding place value and the operation in question. Plus, repetition and practice with novelty and choice.
Thanks for this distinction, Declan!