My favorite of all the Depth of Knowledge (DOK) levels, as I define them in these matrices for elementary and secondary mathematics, is DOK 3. I’ve always found it challenging to give a short and sweet reason as to why I felt that way… until I heard Bushnell’s Law.
This “law” was created by Atari founder Nolan Bushnell and was used to describe his ideal video game. He said:
All the best games are easy to learn and difficult to master. They should reward the first quarter and the hundredth.
When I first heard his law, I thought “That is exactly why I love DOK 3!!” Yes, I realize how nerdy that is, but I’ve learned to embrace it. To explain what I mean, try solving the problem below:
Using the digits 1 to 9, at most one time each, place a digit in each box to make a sum that is as close to 1000 as possible.
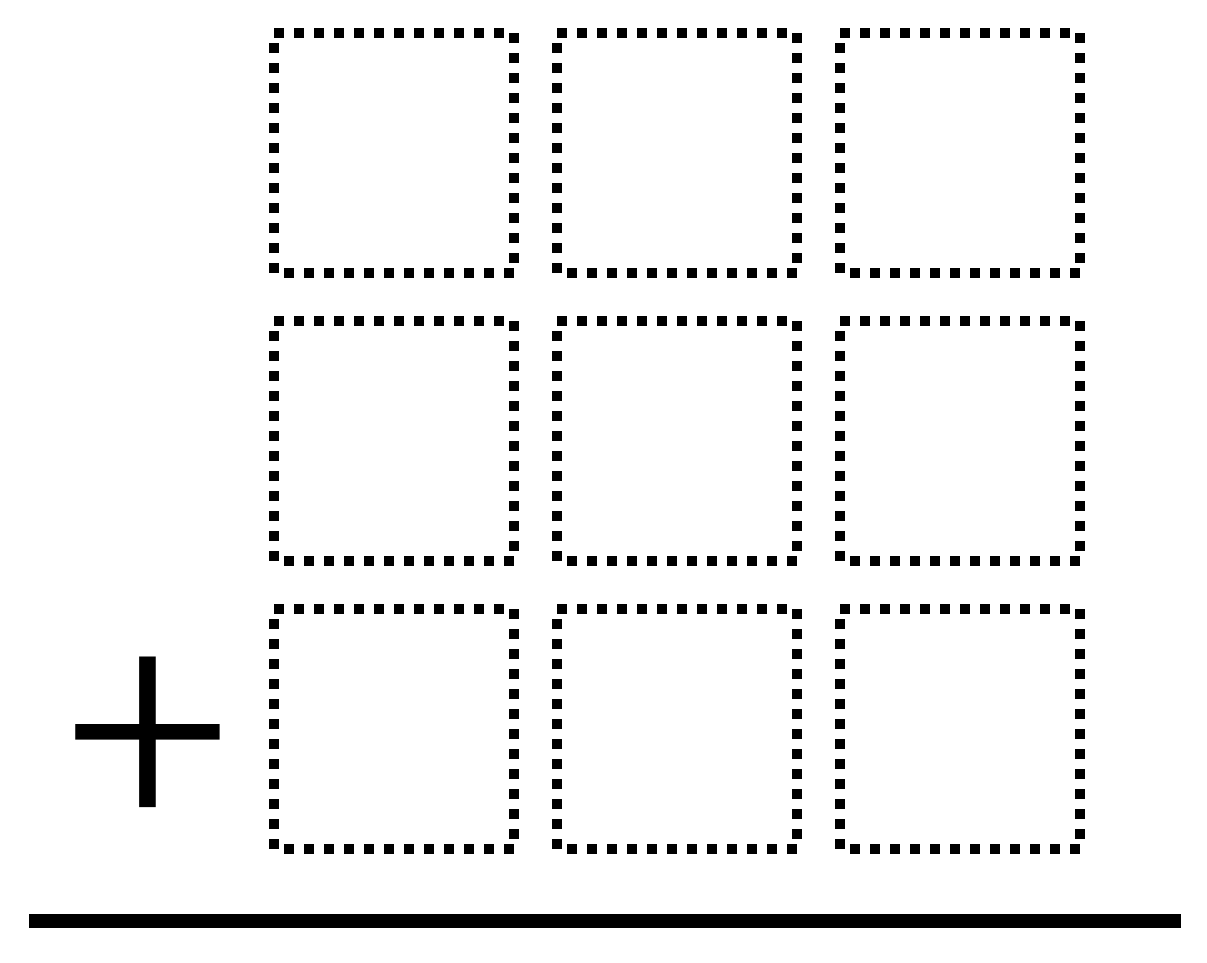
This is the kind of problem that takes people many attempts to figure out. So, when you’re ready to see the answer to this problem, head over to Open Middle.
What do you think? How do you describe problems like these? Let me know in the comments.


I really appreciate the elegant description of these types of problems as “Easy to learn and difficult to master” much more than the old saying “very low floor and high ceiling” because this new description is much easier to use within the classroom setting with students of ALL ages and abilities. The students better understand the depths in which we are all able to go as we dig into mathematics when they are supported by this idea. Many students from various backgrounds, life experiences, who may be our ELLs or MLLs, as well as our students with learning disabilities and accelerated learners are able to learn how to begin math problems with relatively no problem and with ease. However, when many of these students are asked to use the application of math models, math strategies, or written explanations to help explain their thinking and prove their work this math task or math problem suddenly makes students frustrated and no longer confident in their math skills even though they may be able to set-up the problem correctly and even get the correct answer. I have had many highly intelligent students explain to me that they can just do the math, but they can’t explain the how or the why behind their work. For this reason, I encourage ALL students and teachers at all ability levels to explore their deeper understanding of math problems by getting the manipulatives and drawing paper out of the cupboards and having them always out and ready to be used for math problem exploration and explanations.
Thanks for unpacking this, Sarah. The familiar reality of “they can just do the math, but they can’t explain the how or the why behind their work.” speaks volumes about what our priorities have traditionally been in math education. Undoing that to reprioritize things like explaining your thinking or applying mathematics (via math modeling) won’t happen overnight, unfortunately.