How Many Hanukkah Candles Will We Need?

 

 

• How many Hanukkah candles will we need?
• How many Hanukkah candles would we need if Hanukkah lasted 10 nights? 50 nights? n nights?

 

We begin this problem by thinking like a spy and figuring out what information we have and what information we need. The video shows us that candles are being lit and the beginning of what might be a pattern. Initially, students may not be aware of what information they know and what information they need to know. Having students make an estimate is a great way to get that process going.

If you’re not already using a Problem Solving Framework with your students, it has a section where they can list their low, high, and best estimate. For example, a student might pick 5 candles for for a low estimate (“It has to be at least 5 candles!”), 100 candles for a high estimate (“There’s no way they’re using more than 100 candles”), and 30 candles for a best estimate.

One of the great parts of this process will be students saying things like “How are we supposed to know how many candles we’ll need? We need to know ____________________, ____________________, and ____________________.” This is exactly where you want them because now they’re both interested in the context and ready to control how the problem solving continues.

They may ask for some or all of the following information, but only give them what they ask for. They need to learn what information they need.

Why are they lighting candles?
Hanukkah (pronounced ha-new-kuh) is a Jewish holiday which remembers what was viewed a miracle when a day’s supply of oil remained lit for eight days. To celebrate, candles are lit for eight nights on a candle holder called a menorah (pronounced meh-nor-uh).

How many candles are lit on each night?
A Hanukkah menorah has nine places to put candles. One is for the shamash (shuh-mah-sh) which is the helper candle used to light the other candles and the other eight represent the eight nights. On the first night, one candle and the shamash are used for a total of two candles. On the second night, two candles and the shamash are used for a total of three candles. This continues until the eighth night where nine candles are used.

 

With this information, students should now shift towards thinking like an analyst and come up with strategies for solving the problem. Here are a few that students might use.

Count all
Students might draw out all the candles used on each night and then count them one at a time, up to 44. This will definitely work but will be slow and often may lead to miscounting.

Adding consecutive nights together
Students might add each night, one at a time. For example they might start with 2 candles on night one + 3 candles on night two = 5 total candles. Then do 5 total candles + 4 candles on night three = 9 total candles. This would continue until all 44 candles are counted. This works as well but sometimes the numbers are not as easy to count together.

Making tens
Students frequently like to make tens, and they may notice that in the list of 2, 3, 4, 5, 6, 7, 8, and 9, they could pair up 2 and 8, 3 and 7, and 6 and 4. That gives them 30 + 5 + 9 for a total of 44 candles.

Gaussian strategy
This problem reminds me of the story of Carl Friedrich Gauss whose teacher told him to find the sum of all the whole numbers from 1 to 100. He saw that he could make fifty pairs of numbers (like 1 and 100, 2 and 99, 3 and 98, … 49 and 52, and finally 50 and 51) and that their sum would be 101. 50 x 101 gave him 5050.

We have a similar opportunity with this problem. The candles used on each of the eight nights are 2, 3, 4, 5, 6, 7, 8, and 9. These form four pairs of numbers that equal 11 (2 and 9, 3 and 8, 4 and 7, and finally 5 and 6). This gives us 4 x 11 or 44 candles needed.

When students are ready, you can show them this video so they can see the results.

An interesting extension for this problem that’s great for high school students is figuring out how many candles we would need if Hanukkah lasted longer than 8 nights. For example, how many candles would we need if Hanukkah was 10 nights, 50 nights, 100 nights, or n nights long?

There are a variety of ways to approach figuring this out. Some may already know that the sum of 1 + 2 + 3 + … n = n(n+1)/2. With that information, we can plug in (n+1) wherever there is an n. We do this because on each night, one more candle is used than the night number. This gives us (n+1)(n+2)/2. As it turns out, this formula is close but not exact because it’s always 2 more than it should be, so we have to subtract 2, giving us ((n+1)(n+2)-2)/2

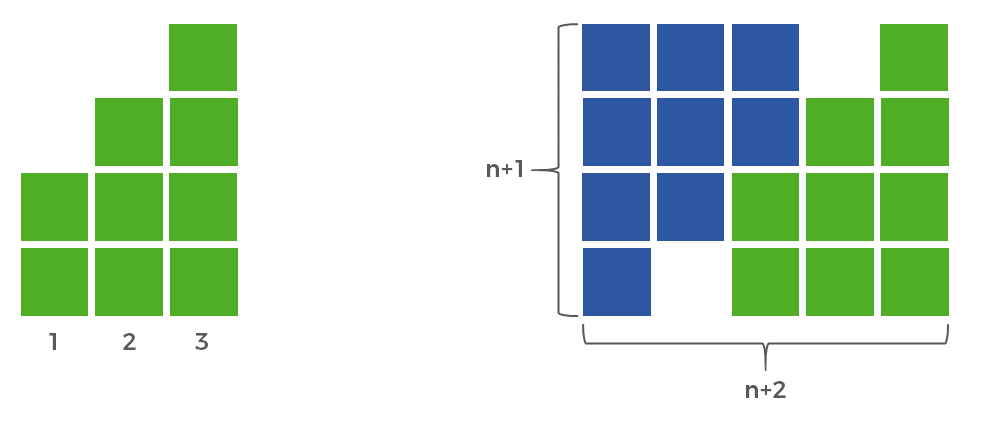
The visual representation below helps make it clear why we need to remove 2 from the total. On the left side in green is a representation of the total candles used in the first three nights. On the right side, I’ve duplicated the green squares in blue and rotated them 180°. Putting them together makes a rectangle that is n+1 on one side (in this case 4) and n+2 on the other side (in this case 5). However 2 squares are missing because we started each with 2 candles, not 1. This gives us an area of (n+1)(n+2)-2. Ultimately, we only want half of these squares and so we divide it all by 2 to give us ((n+1)(n+2)-2)/2.

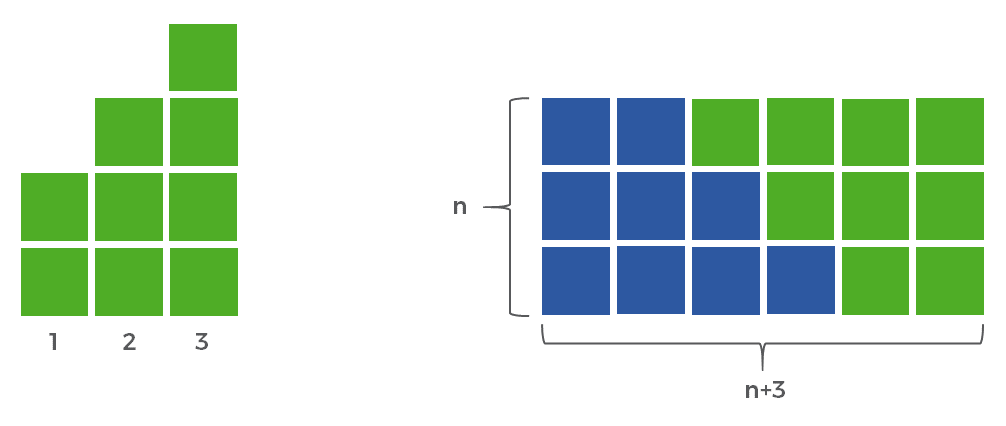
Another way we could have represented this function is by simplifying ((n+1)(n+2)-2)/2 to get n(n+3)/2. So let’s look at a visual representation of that as well. On the left side is the same green representation of the total candles used in the first three nights. On the right side, I’ve again duplicated the green squares but this time rotated them 90° counterclockwise and made a copy as blue squares which I rotated 90° clockwise. Putting them together makes a rectangle that is n on one side (in this case 3) and n+3 on the other side (in this case 6). Again, we only want half of these squares and so we divide it all by 2 to give us n(n+3)/2.

 

• 4.OA.5 – Generate a number or shape pattern that follows a given rule. Identify apparent features of the pattern that were not explicit in the rule itself. For example, given the rule “Add 3” and the starting number 1, generate terms in the resulting sequence and observe that the terms appear to alternate between odd and even numbers. Explain informally why the numbers will continue to alternate in this way.
• 8.F.4 – Construct a function to model a linear relationship between two quantities. Determine the rate of change and initial value of the function from a description of a relationship or from two (x, y) values, including reading these from a table or from a graph. Interpret the rate of change and initial value of a linear function in terms of the situation it models, and in terms of its graph or a table of values.
• F-BF.2 – Write arithmetic and geometric sequences both recursively and with an explicit formula, use them to model situations, and translate between the two forms.

 

Since recording this video, people have let me know that the way I lit the candles is not correct and that they are supposed to be lit from right. This video shows the way I have been doing it since I was a child, and no disrespect was intended.