How Can You Win Every Prize At Chuck E. Cheese’s?

 
Chuck E. Cheese’s (and many other arcades) have a game called Skee Ball where you roll a ball up a ramp and into a hole to earn points.  You earn more points when the ball goes into smaller holes.  The more points you earn, the more tickets you get to buy prizes with.  As a bonus, if you earn at least 450 points, you win their grand prize which gives you as many as thousands of tickets.
 

• How can you get 450 points playing Skee Ball and win the grand prize?

 

These questions may be useful in helping students down the problem solving path:

• How can you score at least 450 points using nine rolls?
• What strategy would you use to earn that score?

 

First, some background and assumptions on Skee Ball:

• One round of Skee Ball uses 9 balls.  In reality kids often throw the balls into another lane so sometimes you have more or less than 9.  The game ends when 9 balls go back into the machine, so throwing additional balls from other lanes is not an option for getting more points.
• Earning 100, 50, 40, 30, and 20 points is fairly obvious as the ball has to go down the corresponding hole.  However, when you don’t make it into 100, 50, 40, 30, or 20 points, there is a big curve to catch all the falling balls.  This curve empties into the 10 points hole.  So, if you miss one of the higher scoring holes, you will almost always earn at least 10 points when it falls down.
• I am assuming cheating (such as in the picture below where the child walks up the ramp and drops the ball into the hole) is also not an option.
• The grand prize goes up one ticket every time someone plays the game without winning the grand prize.  So, it could conceivably go very high.  When the grand prize is won, it goes back down to 100 tickets so it is still a good bonus.  You also win the tickets for the 450 points.
• Order doesn’t matter.  So rolling four 100’s followed by five 10’s is the same as rolling five 10’s and then four 100’s.

This problem can be done using only elementary standards to decompose numbers.  Alternatively, it can also be done using systems of equations and the graph provides an interesting context.  Let’s start first with the decomposition.

By asking students, “How can you score at least 450 points using nine rolls?”, students will have to decompose 450 and account for the nine rolls.  To be clear, this is different than the question, “What are all the ways you can score at least 450 points using nine rolls?”  That question could send the lesson into a rather dull place where students list every single possibility.  The two things I hope students get out of the first question are that to get 450 points you have to:

• roll at least one 100 or
• roll nine 50’s in a row

With this knowledge in hand, it is time to use Math Practice 2 again and bring the context back to this problem.  The context will help students think about what path to pursue next.  Let’s explore each of those two possibilities:

• Rolling a 100 is supposed to be the hardest as it has the smallest hole.  If you aim for the 100’s every time, you can earn 450 if you make four out of nine (~44%) into the 100.  The five that missed the 100 will likely fall into 10 hole.  That gives you 450 (4*100 + 5*10).
• Rolling a 50 is supposed to the second hardest as it has the second smallest hole.  If you aim for the 50’s every time, you have no margin for error.  If you miss a 50, it will fall into something less than 50 and you will not earn enough points.

So basically your choices come down to rolling 44% of your balls into the 100-hole or 100% of your balls into the 50-hole.  What I hope students realize is that even though 100’s are the hardest hole to roll the ball into, it is the only strategy that has a realistic chance for winning the grand prize.  Looking at the pictures, the difference in hole size between 100 and 50 is not that much, and being able to miss over half of your shots when aiming for 100 is a very helpful advantage.

In actuality, this is not just theoretical.  This situation was something I noticed when I was a child and trying to win the prizes.  I found that if I only rolled for the 100s, I could get at least four of my nine rolls to go in the 100-hole and win the grand prize at least once every four or five games.  Unfortunately, back then the best prizes were a mini-basketball and a cereal bowl with Chuck E. Cheese on it.

If you plan on treating this as a systems of equations problem, then your two equations (where x is the number of 10’s rolled and y is the number of 100’s rolled) are:

x + y = 9 (the total number of balls rolled must equal 9)

10*x + 100*y ≥ 450 (the total points must be greater than or equal to 450)

Using Desmos’s graphing calculator, this gives the graph:

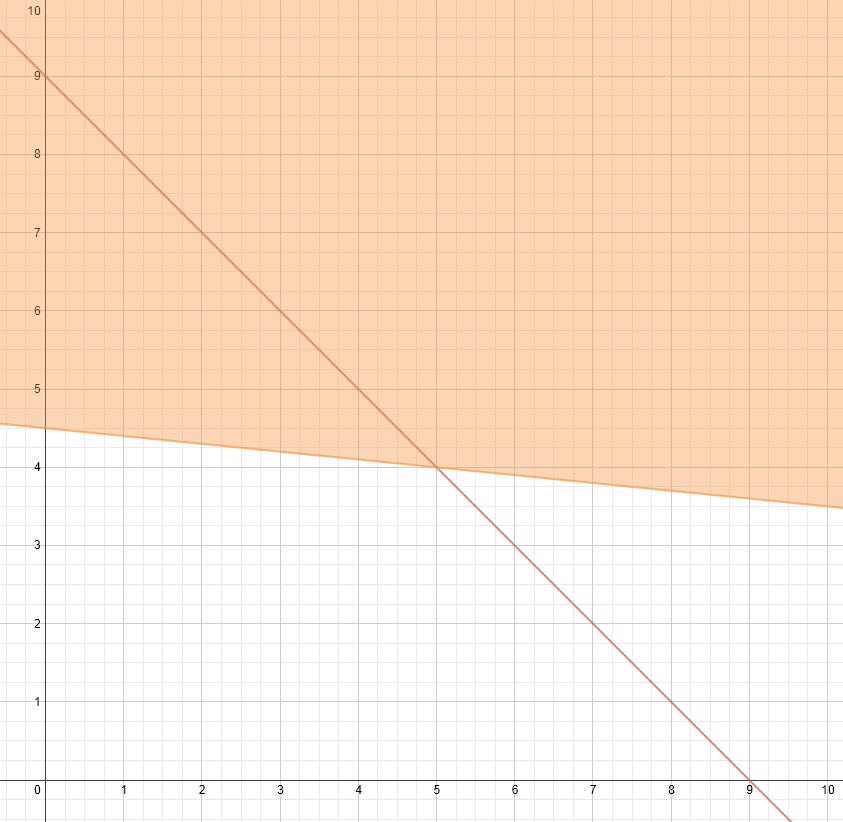
There are several aspects of this graph that are worth getting kids to interpret:

• The x-axis represents the number of 10’s rolled
• The y-axis represents the number of 100’s rolled
• The line x + y = 9 represents that the total number of balls must equal 9.  In actuality, this is really a discrete set of points rather than continuous.
• The region shaded above the inequality 10*x + 100*y ≥ 450 represents total scores that are at least 450 points.  So, only the games where there are at least four 100’s are going to score at least 450 points.
• The equation and inequality intersect at (5, 4).  This represents that you could get five 10’s and 4 100’s and get exactly 450 points.

As an extension to this problem, I have provided a picture of how Chuck E. Cheese’s currently runs their Skee Ball game.  Some noteworthy changes include:

• All of the scores are 100 times higher.  It is a proportional change and doesn’t change anything about the results.  You still need to roll four 10,000’s and five 1,000’s to get 45,000 points.
• That being said, they have made the score needed to win the grand prize adjustable.  In the current picture it is set for 46,000 and you win 75 tickets.

• Child cheating and sign that says “ACHIEVE A SCORE OF 450 TO WIN” with 139 tickets being the current grand prize.

• The old Skee Ball scoring system was 10, 20, 30, 40, 50, and 100.

• The new Skee Ball scoring system is now 100 times higher with 1,000, 2,000, 3,000, 4,000, 5,000, and 10,000.

 

• CCSS 2.NBT.7 Add and subtract within 1000, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method. Understand that in adding or subtracting three-digit numbers, one adds or subtracts hundreds and hundreds, tens and tens, ones and ones; and sometimes it is necessary to compose or decompose tens or hundreds.
• CCSS 3.NBT.2 Fluently add and subtract within 1000 using strategies and algorithms based on place value, properties of operations, and/or the relationship between addition and subtraction.
• CCSS 3.NBT.3 Multiply one-digit whole numbers by multiples of 10 in the range 10–90 (e.g., 9 × 80, 5 × 60) using strategies based on place value and properties of operations.
• CCSS 8.EE.8c Solve real-world and mathematical problems leading to two linear equations in two variables. For example, given coordinates for two pairs of points, determine whether the line through the first pair of points intersects the line through the second pair.
• CCSS A-CED.3 Represent constraints by equations or inequalities, and by systems of equations and/or inequalities, and interpret solutions as viable or nonviable options in a modeling context. For example, represent inequalities describing nutritional and cost constraints on combinations of different foods.
• CCSS A-REI.11 Explain why the x-coordinates of the points where the graphs of the equations y = f(x) and y = g(x) intersect are the solutions of the equation f(x) = g(x); find the solutions approximately, e.g., using technology to graph the functions, make tables of values, or find successive approximations. Include cases where f(x) and/or g(x) are linear, polynomial, rational, absolute value, exponential, and logarithmic functions.
• CCSS F-BF.1 Write a function that describes a relationship between two quantities.
• CCSS F-IF.4 For a function that models a relationship between two quantities, interpret key features of graphs and tables in terms of the quantities, and sketch graphs showing key features given a verbal description of the relationship. Key features include: intercepts; intervals where the function is increasing, decreasing, positive, or negative; relative maximums and minimums; symmetries; end behavior; and periodicity.
• CCSS F-IF.5 Relate the domain of a function to its graph and, where applicable, to the quantitative relationship it describes. For example, if the function h(n) gives the number of person-hours it takes to assemble n engines in a factory, then the positive integers would be an appropriate domain for the function.
• CCSS F-IF.6 Calculate and interpret the average rate of change of a function (presented symbolically or as a table) over a specified interval. Estimate the rate of change from a graph.

 

• Chuck E. Cheese’s
• Desmos’s graphing calculator