How Big Are Sunspots?

 
Sunspots create solar flares that can damage satellites in orbit, disable GPS systems, and cause power failures in cities.  The larger the sunspot, the higher the chance of creating a powerful solar flare.
 

• How big is Sunspot AR 1476?

 

These questions may be useful in helping students down the problem solving path:

• What is a guess that is too low?
• What is a guess that is too high?
• What is your best guess?
• What information would be useful in figuring this out?
• How can we convert units to make this something that is easier to understand?
• How do you think scientists classify sunspots to determine which are the biggest?

 

Below is a picture of the sun taken on May 10, 2012 from Space.com.  The cluster of sunspots closest to the center of the image is Sunspot 1476.  I suggest beginning by giving students a printout of the image and having a conversation about what sunspots and solar flares are.  The videos in the “What You’ll Need” section will be helpful for that.

I have intentionally chosen “big” as part of the challenge question as it is mathematically imprecise.  I hope it forces a conversation to add some clarity.  “Are we measuring the sunspot’s width/length/height/diameter/area/volume?” “What units should we measure the sunspot with?”  It will be a great opportunity to understand the value of Math Practice 6 where students need “to communicate precisely to others”.

My thoughts on the above questions:

“Are we measuring the sunspot’s width/length/height/diameter/area/volume?”
This really depends on what you are measuring.  Sunspot AR 1476 looks something like snake with a large head.  Students should decide whether they are measuring the entire snake, just its head, or both.  Once that has been decided, students need to determine what dimension of the sunspot we are measuring.  This is a good opportunity for students to think like a scientist.  “How do you think scientists classify sunspots to determine which are the biggest?”  Hopefully students will realize that measuring its volume is unrealistic.  The only realistic options that are left are measuring its area or length.  Measuring its area would be the most accurate and challenging route due to its irregular shape.  For the purposes of this lesson, I recommend using the less accurate but reasonable length measurement.

“What units should we measure the sunspot with?”
This is another important question that can be answered in many ways.  The main issue here is that the numbers students will work with will be so big that they will lose perspective.  For example, if they choose inches, will a student appreciate the difference between one billion and one trillion inches?  So, at a minimum I would recommend a larger unit like miles or kilometers.  Realistically, those will also be too small of a unit as once you have over 1000 miles or kilometers, it will be challenging for students to appreciate the difference.  The next step would be using non-standard units of measurements such as:

• Distance across the United States (pick two arbitrary cities and find their distance)
• Distance around the Earth (Earth’s circumference)
• Distance from the Earth to the Moon
• Earth (or more specifically Earth’s diameter)
• Jupiter (or more specifically Jupiter’s diameter)

Clearly this is not a comprehensive list, but they may help students better appreciate how truly massive Sunspot AR 1476 really is.

One additional piece of information to be aware of going into this lesson is that planets and stars are not perfect spheres.  They are actually called spheroids as shown in the picture below.  As they rotate, their equators stretch out slightly and their radius is actually larger at the equator than at the poles.  Accordingly, you will see phrases like “mean diameter”, “mean radius”, “equatorial radius”, and “polar radius”.  Since the shape’s diameter or radius changes depending on where you are looking, the “mean” provides the average length versus the length at the equator or magnetic poles.

With this in mind, students will need to begin by determining Sunspot AR 1476’s size in relation to the Sun’s size.  One method is to set up a proportion between the sun and sunspot using the image and actual distance measurements.  The image below contains information from Wikipedia that students will need.  Note that I have blacked out five areas that reference how many times bigger that measurement is than the respective measurement of the Earth.  There is also a version of this image with all the information showing in the “What You’ll Need” section.

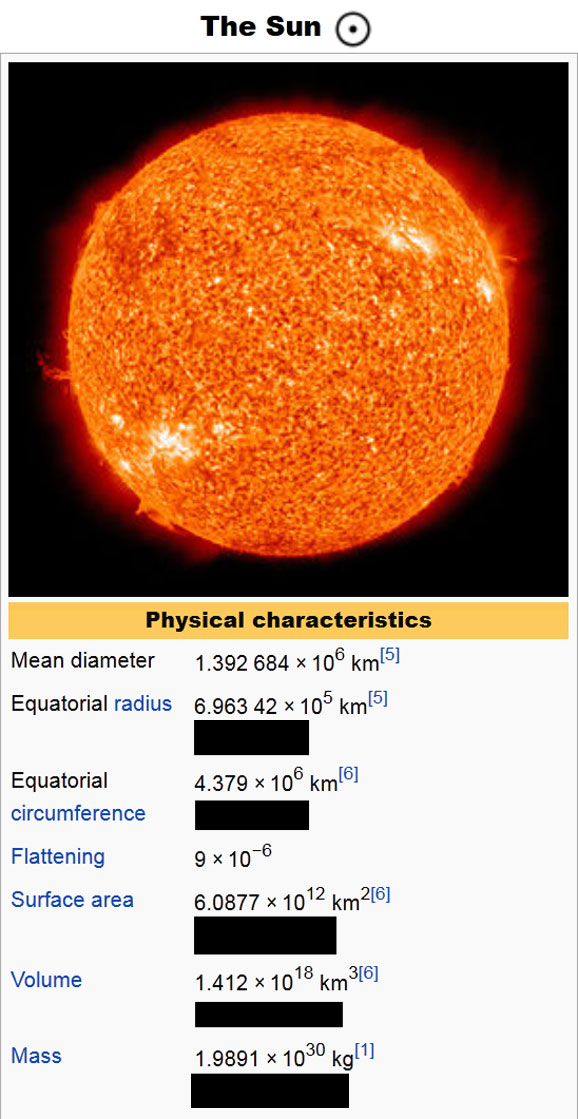
When I measured the sun and sunspot on a printed sheet of paper, I measured the entire sunspot cluster (the complete snake) as 2.5 cm and the main sunspot cluster (the snake’s head) as 0.9 cm.  I measured the sun’s diameter as 17.5 cm.  With that information I determined:

Entire Sunspot Cluster
2.5 cm / 17.5 cm ≈ 0.142857 (meaning the sunspot is about 14.2857% of the sun’s diameter)

Main Sunspot Cluster
0.9 cm / 17.5 cm ≈ 0.051428 (meaning the sunspot is about 5.1429% of the sun’s diameter)

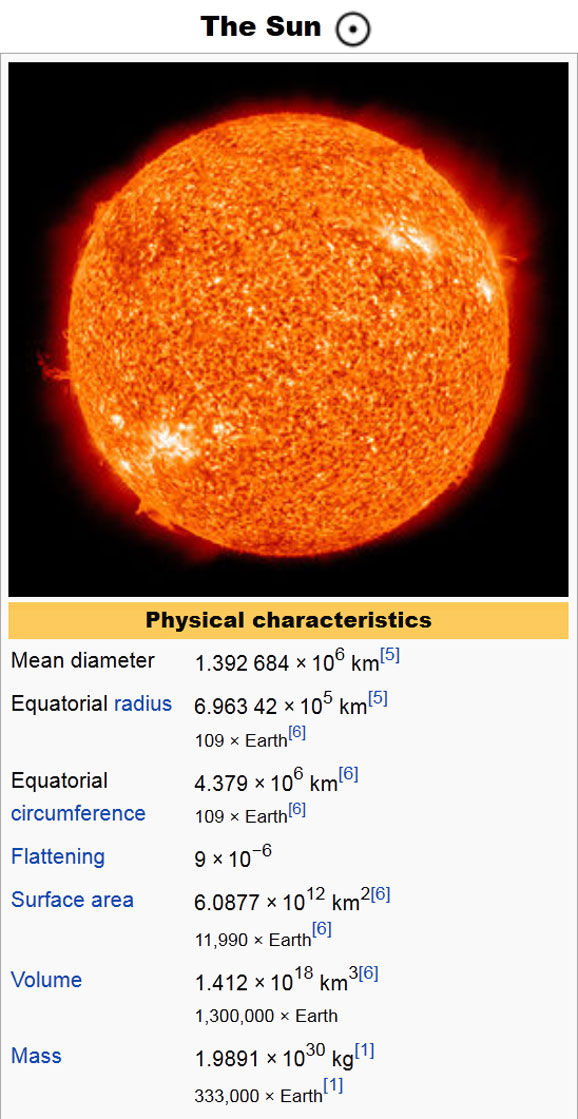
From the Wikipedia information, the sun’s diameter is 1.392684 x 10^6 km or 1,392,684 km long so:

Entire Sunspot Cluster
0.142857 * 1,392,684 km ≈ 198,955 km

Main Sunspot Cluster
0.051428 * 1,392,684 km ≈ 71623 km

Students may struggle with Math Practice 2 at this point as those lengths are so large that they may not be able to make sense of them.  Specifically, Math Practice 2 states that “quantitative reasoning entails habits of … considering the units involved; attending to the meaning of quantities, not just how to compute them.”  So, while it may seem that we have reached our answer, if we are only computing them and not also attending to their meaning, we are missing part of the goal.

As such, let’s consider these lengths in different units:

• Distance across the United States (4,488 km from Los Angeles to New York)
• Distance around the Earth (40,075 km)
• Distance from the Earth to the Moon (384,400 km)
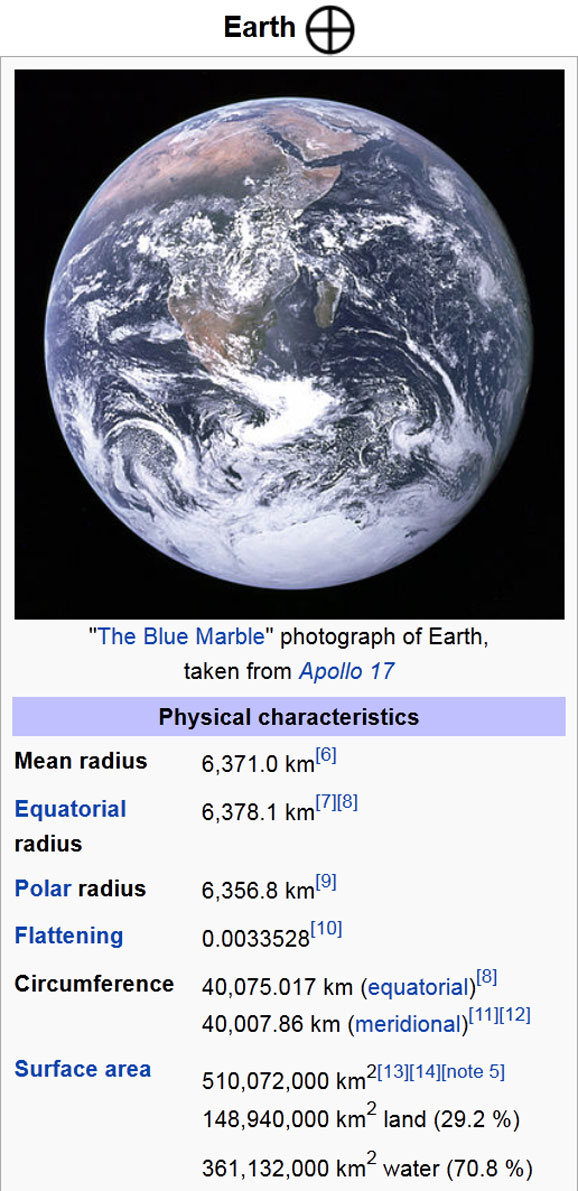
• Earth (Mean diameter is about 12,742 km)
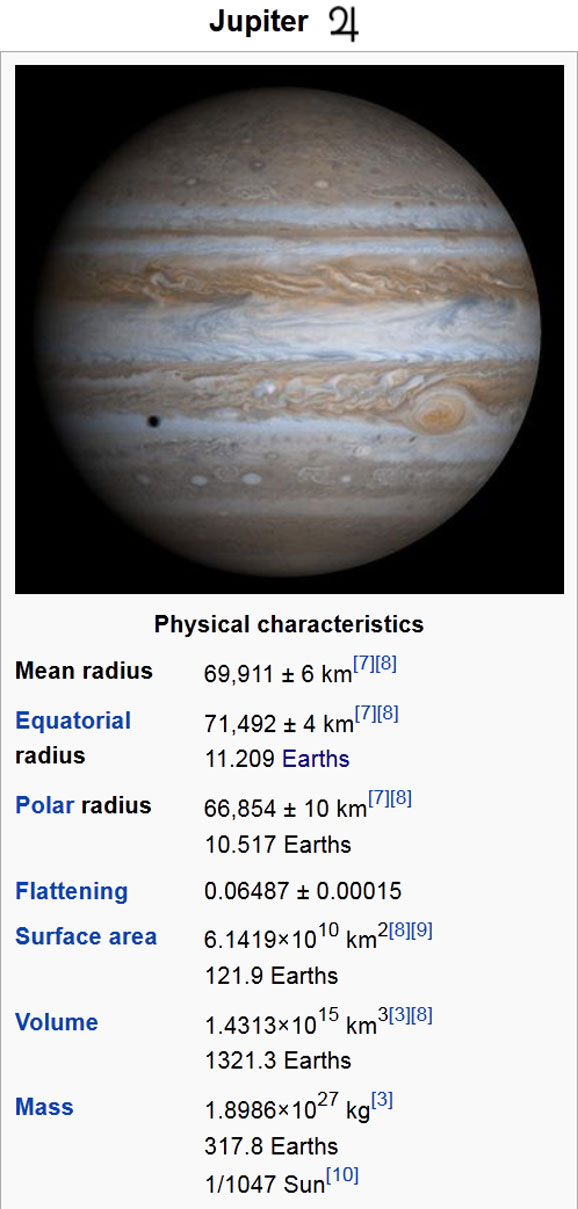
• Jupiter (Mean diameter is about 139,828 km)

 

Entire Sunspot Cluster

• ~44 trips between Los Angeles and New York
• ~5 trips around the Earth
• ~.5 trips from the Earth to the Moon
• ~15.6 Earths
• ~1.4 Jupiters

 

Main Sunspot Cluster

• ~16 trips between Los Angeles and New York
• ~2 trips around the Earth
• ~.2 trips from the Earth to the Moon
• ~5.6 Earths
• ~.5 Jupiters

 

These units should put Sunspot AR 1476’s massive size in better perspective.  You could even have a conversation as to which units are more or less useful.  Something to note for perspective is this quote from EarthSky:

This monster region of sunspots on the sun’s surface – AR 1476, as long as 10 planet Earths – has been turned in Earth’s direction
this week.

It would be a valuable conversation to discuss how her measurement “as long as 10 planet Earths” differs from ours of 15.6 (entire sunspot cluster) to 5.6 (main sunspot cluster).  Possibilities include:

• The sunspot’s size changed
• She is measuring different parts
• She is averaging the two measurements
• Measuring the surface area of a sphere on a two-dimensional piece of paper causes measurement errors

It would also be good to throw in some potential misconceptions here.  Could her answer be different because:

• She measured in miles?
• Her initial measurements were slightly different than ours?

 

As a visual comparison, here are two images from Space.com comparing Sunspot AR 1476 to Earth and Jupiter:

• Earth compared to Sunspot AR 1476

• Jupiter compared to Sunspot AR 1476

 

One last note to consider.  From spaceweather.com (which wrote this before AR 1476 was observed):

“Astronomers measure the sizes of sunspots as fractions of the Sun’s visible area. Their favorite units are ‘millionth’s.’ A sunspot that registers 1 millionth has a surface area equal to 0.000001 times the area of the Sun’s Earth-facing hemisphere. Typically, a big sunspot measures 300 to 500 millionths. The entire surface area of the Earth is only 169 millionths of the solar disk.  On March 29, 2001, active region 9393 became the biggest sunspot since 1991. The behemoth spot registered 2400 millionths, or 14 times larger than Earth.”

AR 9393 seems to be larger than AR 1476 but still comparable.  So, if students are curious about what units scientists actually use, “millionths” is the answer.
 

• Sun information from Wikipedia

• Earth information from Wikipedia

• Jupiter information from Wikipedia

• AR 1476 emitting solar flares

 

• Sunspot AR 1476 from Space.com

 

• CCSS 5.MD.1 – Convert among different-sized standard measurement units within a given measurement system (e.g., convert 5 cm to 0.05 m), and use these conversions in solving multi-step, real world problems.
• CCSS 7.RP.2 – Recognize and represent proportional relationships between quantities.
• CCSS 7.G.4 – Know the formulas for the area and circumference of a circle and use them to solve problems; give an informal derivation of the relationship between the circumference and area of a circle.
• CCSS 8.EE.4 – Perform operations with numbers expressed in scientific notation, including problems where both decimal and scientific notation are used. Use scientific notation and choose units of appropriate size for measurements of very large or very small quantities (e.g., use millimeters per year for seafloor spreading). Interpret scientific notation that has been generated by technology
• CCSS G-MG.1 – Use geometric shapes, their measures, and their properties to describe objects (e.g., modeling a tree trunk or a human torso as a cylinder).

 

• EarthSky
• Wikipedia – Sun
• Wikipedia – Earth
• Wikipedia – Jupiter
• Space.com
• NASA’s Helioviewer
• spaceweather.com