Here’s a question to think about: if you completely remove a problem’s context and can still solve it, can it really be mathematical modeling?
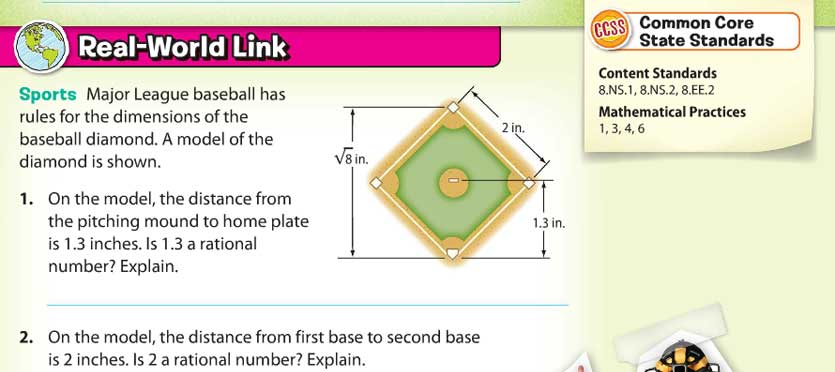
Consider the math problem below from a middle school math textbook. It uses the context of a baseball diamond to discuss rational numbers. It is listed as a “Real-World Link” and demonstrating Math Practice 4 (notice the box in the upper right).

I was watching students work on this page and wondered how important the context was to solving these problems. Then it made me wonder, “What if there was no context? What would change?” This is what the problem might look like it the context was completely removed.

To me, it looks like the context is completely unnecessary to do all of the problems. This is not mathematical modeling.
It reminds me of what the California Department of Education lists under “What Mathematical Modeling Is Not“ (page 2 of this PDF). That document states that mathematical modeling is not “starting with a real-world situation and solving a math problem. Modeling returns students to a real-world situation and uses mathematics to inform their understanding of the world.”
To be clear, I am not saying that creating problems is easy. I am also not saying that all my problems are perfect. What I am trying to say is that we need to carefully look at the problems we choose to make sure that they are likely to accomplish the goals we are hoping for.
If you’re looking for more investigations, Dan Meyer shares his thoughts on some dubious contexts and how to improve existing problems.
Do you have any other examples of fake mathematical modeling problems you’ve seen? Please let me know in the comments.

This issue seems to have come up a lot recently, so I’ve noticed a pattern: I really hate bad contexts.
You write: “it looks like the context is completely unnecessary to do all of the problems.”
I would go farther: this context is harmful. The context creates a conflict between the specific new material (rational vs irrational numbers) and other important concepts (measurement and measurement error). Subtly, we are discouraging students from
(a) forming connections across topics. For my taste, surprising connections has to be one of the most beautiful and delightful aspects of math.
(b) using all of their ideas and creativity to understand a challenge.
(c) putting new mathematical ideas into a broader mathematical context (maybe I’m just repeating point a?)
I admit that the example only touches on these points lightly, but I suspect the accumulated weight over the course of a school math education is substantial.
If I were full-time in a classroom with a textbook, I’d be tempted to use it as follows:
1. create censored versions of all problems and examples (as you did)
2. work through the questions with the kids
3. Ask them what context they think the publishers originally included and why
4. show the published version
5. discuss (does the published version relate to the math, does it help them understand, does it add confusion, does it conflict with something they know, etc)
Thanks Joshua. I appreciate you sharing lots of interesting thoughts to reflect on. Dan Meyer has done some similar things as you suggest about revealing information and gradually releasing more of it as students realize that they need it and wonder about it. Be sure to check it out if you haven’t already.
I tested my proposed lesson with the censored page and then the published page on my two kids, ages 7 and 9. I don’t know if this was particularly fair or unfair on the publisher, since my kids don’t really know about baseball. However, they both agreed that the pictures didn’t add anything. Choice quote, pointing to the umpire: “Daddy, what does that man have to do with rational numbers?”
I was initially skeptical about using the calculator for sqrt(8) as well, but that triggered an unexpected bonus. They’d keyed in something incorrectly and got 1.something. Before I could comment, one of them recognized that couldn’t be right and they did a quick estimate: “it should be more than 2 but less than 3.”
Wow! Any 7 or 9 year old who can reason independently about square root approximations is pretty awesome in my book!
I do agree that it is a hard test to apply to a textbook. They certainly have the challenge of balancing demands from teachers with what is reasonable to create. I’m just trying to help educators have a discerning eye when choosing problems.
Based on the context of this particular problem, “model” appears to refer to a scale model, not the modeling process.
I didn’t even realize that Geoff. That’s a great point and something I’m wondering about. Perhaps the problem’s author didn’t have a firm understanding of what makes a problem truly mathematical modeling.
The mathematical practices listed in the upper right corner are covered throughout the lesson. You would need to check the lesson plan specifics to ensure this particular problem is he one hey are referencing for MP 4. I’d predict MP 4 is addressed in one of the HOT (higher order thinking) problems.
Hi Erica. That’s a good point and I didn’t know whether you were right or not so I went looking at the book to verify your prediction. Here’s what I found.
There was another “Real World Example” that states: “On a clear day, the number of miles a person can see to the horizon is about 1.23 times the square root of his or her distance from the ground in feet. Suppose Frida is at the Empire State Building observation deck at 1,250 feet and Kia is at the Freedom Tower observation deck at 1,362 feet. How much farther can Kia see than Frida?” This also would not be mathematical modeling as the model (distance a person can see to the horizon = ~1.23 * √distance from the ground) is given to them, not something students are deriving.
There was a H.O.T. Problem that was labeled as “Model with Mathematics” that said “Identify two numbers, one rational number and one irrational number, that are between 1.4 and 1.6. Include the decimal approximation of the irration number to the nearest hundredth.” While this may be “Higher Order Thinking”, it is not mathematical modeling.
So, based on this, my conclusion is that even if Math Practice 4 was meant to be applied to the whole lesson and not that single problem, I still don’t see it.
Again, it isn’t my intention to make a publisher feel bad. It also isn’t my intention to say that every problem from this or other publishers are bad. In fact, I’d have a very hard time coming up with a problem for many contexts (such as polynomial operations). That being said, it is my intention to help educators be more discerning when choosing problems.
This problem, as well as other “Real World Examples” in this textbook are from the opening page of the lesson. I have used this series/textbook in my room. This first page is generally a warm-up/introduction page with a problem/definition/diagram at the top of the page and then the Real World problem at the bottom to get the students to begin to think about the upcoming math and activate prior knowledge. The SMPs listed on this page are the standards and practices that are seen during the lesson and practice problems.
“There was a H.O.T. Problem that was labeled as “Model with Mathematics” that said “Identify two numbers, one rational number and one irrational number, that are between 1.4 and 1.6. Include the decimal approximation of the irrational number to the nearest hundredth.” While this may be “Higher Order Thinking”, it is not mathematical modeling.”
As for the HOT problems, they are problems that are included in the Independent practice pages at the end of the lesson. It has been my experience that there is more to the HOT problem than what you listed. They are not easy and do require the students to multiple steps in order to persevere in their problem solving. I’d bet that the problem you identified either had a number line or additional directions somewhere to include SMP4.
That has been experience at least using this textbook series.
Hi Shannon. I appreciate you sharing your perspective. Let me clarify what I’m trying to say. I am not trying to say that H.O.T problems are not valuable or that I have completely described all varieties of them. What I am trying to talk about specifically is doing justice to mathematical modeling.
I believe that the problem I have shared is not mathematical modeling. I did not find any other examples of mathematical modeling anywhere else in this part of the book, including the H.O.T problem that was labeled as “Model with Mathematics”. Again, I am not saying that it is not a worthwhile problem, it is just not mathematical modeling.
You also mentioned, “I’d bet that the problem you identified either had a number line or additional directions somewhere to include SMP4.” Perhaps I am misunderstanding you, but simply including a number line in a problem or requiring students to use a number line does not make it mathematical modeling. That also reminds me of the document I shared about “What Mathematical Modeling Is Not“ where it states that it is not “Using a graph, equation, or function and calling it a model. True modeling is a process.”
As an example of what mathematical modeling is, consider the Home Run Derby. How challenging must it be to determine how far a home run was hit since it usually hits a wall or the stands? Creating the formula must be crazy! It’s the creation of that formula that is an example of mathematical modeling. If someone gave you the formula and you used it, that would not be mathematical modeling as the model was already created for you. You might use a number line, for example, in figuring out how far the ball was hit. However, just using a number line doesn’t make it mathematical modeling.
This reminds me of the time that I got dinged on an observation for not using problems in context. The topic that day was adding rational expressions (8th-grade Algebra 1). The only problems I had been able to find were ones like “The production in a factory is given by (rational expression) and by (rational expression). What is the total production?” Since they were bogus, I didn’t use them. I later asked the Calculus teacher what I could have used and he said he couldn’t think of anything that would have made sense for my students and that the only ones he had seen were the same ones I mentioned. Would you agree that some of the things we teach are just tools for the toolbox that they will use later in abstract problems? (This is also why I’m glad I switched to sixth-grade math. It’s easier to find good contexts for what I teach them.)
Oh, you may have already answered my question above when you said “In fact, I’d have a very hard time coming up with a problem for many contexts (such as polynomial operations).”
Yeah, some topics are more or less suited towards modeling. As you said, the “tools for the toolbox” are generally procedures that may be used as part of the modeling process, but may not have a direct context to modeling itself.
Hello. I apologize in advance if my sentences end up wonky; I need sleep. In any case, you mention that some topics are more suited than others when it comes to mathematical modeling problems. Could you give me an example?
I wandered into this(your) website since we were tasked (high school, allegedly advanced curriculum, basically covers 2 yrs of college within the 6 years of high school (K-12) or something, so idk if stating my school year would allow u to discern uh (my vocab gave up, I miss when I had more than pretty much 10 words in my vocabulary), well, where we are right now.
In any case, it would be very advantageous to know what topic would be a better for the given assignment. You have linked a vid to one of your replies here, so I’ll be checking that out. I’ll also try to look around the website a bit more. But it would be nice to get a direct answer from you. Cheers, mate.
I forgot entire words, awesome.
Thank you for making at attempt at clarifying what a modeling problem really is. I have been writing my own modeling problems along with my colleagues. We teach Integrated Math III. Here are a couple that I thought could be modeling problems, but looking back at it after reading your blog, I’m not sure anymore:
This was in a HW assignment: The image at the right is a side view of the Golden Gate Bridge in San Francisco (image). It is a suspension bridge that has cables that suspend over the road the cars drive on. The two towers rise 152 meters over the road, and they are 1,280 meters apart. The lowest point of the cables between the towers are 4 meters above the road. Write an equation that models the path of the suspension cables between the two towers.
Another one I wrote is for exponential growth/decay:
This one was on our warm up: On January 15, 2018, USA Today reported the fastest growing state is Utah, and the fastest shrinking state is West Virginia.
a. If Utah has a population of 3,050,000 (3.05 million) and it is expected to grow by 2.03% in one year, approximately what will be the population one year from now?
b. If West Virginia has a population of 1.83 million and it is expected to decrease by 0.54% in one year, approximately what will be the population one year from now?
When I wrote these, I googled all the information for each situation and my intent was for students to see how the skills they are learning can be applied to real life.
Am I on the wrong track here? What suggestions do you have for tasks that I write for lessons?
Thank you in advance for any insights or guidance. 🙂
Hi Essie. Have you seen this webinar? https://robertkaplinsky.com/webinar
I think it does the best job of explaining what math modeling is (rather than what it is not). Check it out and let me know what you think.
I agree that the picture as drawn does not constitute a good model and really does not help the problem. At least if the picture was labeled with the actual dimensions of a baseball diamond, students would learn something about the size of a real diamond. The scale model dimensions make no sense and there is not even a key to know how many feet an inch represents.
I would say that even if it had the correct baseball diamond dimensions, it wouldn’t make the questions they asked become real mathematical modeling problems.