Of all the habits in Stephen Covey’s book, The 7 Habits of Highly Effective People, the one that has resonated with me the most is Sharpening the Saw. To illustrate this habit, Covey tells the story of a man who was walking through a forest when he came across a frustrated lumberjack.
Don’t you hate when your lessons are derailed and don’t go as you planned? Wouldn’t it be nice if you could better anticipate these issues and come up with ideas to lessen or eliminate their impact? If so, here’s an idea to consider that has great potential to help: a pre-mortem.
Every once in a while I’ll work with a teacher who dismisses higher depth of knowledge problems such as those on Open Middle as common brainteasers with limited value. While I understand that Open Middle problems have similarities to brainteasers, I believe that there are significant differences that cannot be overlooked.
Consider the two second grade math problems below:
Here’s a question to think about: if you can completely remove a problem’s context and still solve it, can it really be mathematical modeling?
Consider the math problem below from a middle school math textbook. It uses the context of a baseball diamond to discuss rational numbers. It is listed as a “Real-World Link” and demonstrating Math Practice 4 (notice the box in the upper right).
I was watching students work on this page and wondered how important the context was to solving these problems. Then it made me wonder, “What if there was no context? What would change?” This is what the problem might look like it the context was completely removed.
This is the fourth in a series of interviews with educators who are using #ObserveMe signs and what they’ve learned along the way.
Name: Bill Wietman
Twitter handle: @WWietman
Years in education: 12
Current position: Middle School Assistant Principal
Location: Bismarck, North Dakota
Last week I posted my first attempt to expand upon my previous Depth of Knowledge Matrix that helped make it easier to distinguish between depth of knowledge levels in mathematics. This week I am releasing the secondary mathematics matrix to go with last week’s elementary mathematics matrix.
I’ve decided to expand upon my previous Depth of Knowledge Matrix that helped make it easier to distinguish between depth of knowledge levels in mathematics. While it is still useful, it didn’t cover every grade level and may be too broad in scope. So, I have made two new Depth of Knowledge Matrices: one for elementary mathematics and one for secondary mathematics. This week I am releasing the elementary mathematics matrix and next week will be secondary mathematics.
This is the third in a series of interviews with educators who are using #ObserveMe signs and what they’ve learned along the way.
Name: Kelley Kaminsky
Twitter handle: @Kelley_Kaminsky
Website: https://teachwritenow.blog/
Years in education: 13
Current position: English Teacher / Teacher Leader
Location: Estero, Florida
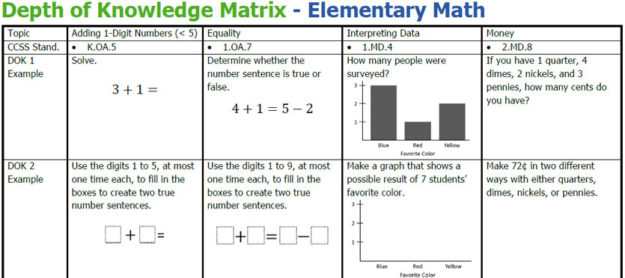
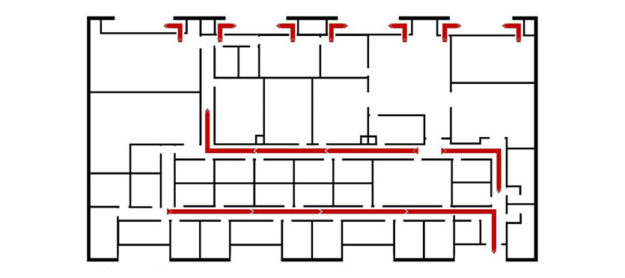
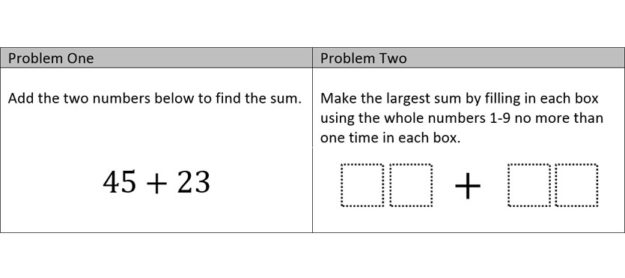
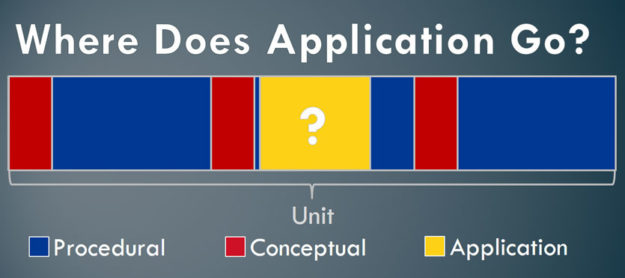
Here’s my first attempt at articulating my thought process behind increasing a procedural problem’s Depth of Knowledge level. It’s not my intention to say that this is the only way to change the level. This is just one way. Also, I am only addressing the DOK level of the math content, not the conversation that students may have around the problem.
I’m starting out with something really basic: single operation problems. In an effort to make this applicable for a K-12 audience, my examples include addition, subtraction, multiplication, square root, exponents, and trigonometry. Clearly six problems won’t apply to every grade level, but I hope they are close enough to what you teach so that you can imagine a version you could use. Specifically, I want to discuss how to take a problem that is primarily a routine procedure and make it more rigorous.
This is the second in a series of interviews with educators who have are using #ObserveMe signs and what they’ve learned along the way.
Name: Sherry Nesbitt
Twitter handle: @snesbitt1972
Website: http://sherrynesbitt.weebly.com/
Years in education: 23
Current position: Middle School Spanish
Location: Hershey, Pennsylvania
This is the first in a series of interviews with educators who have are using #ObserveMe signs and what they’ve learned along the way.
Name: Nate Bowling
Twitter handle: @nate_bowling
Website: http://www.natebowling.com/
Years in education: 11
Current position: AP Government & Politics and AP Human Geography
Location: Tacoma, Washington, USA
I think that professional development providers, certainly including myself, often miss the mark and commit a common mistake when they tell attendees what they need to do but don’t leave them equipped to implement it. To explain this, consider how we teach students what to do during a fire.
The two most common options are providing a map (like you see in hotel rooms) or by simulating the experience through a fire drill (like you see in schools). Giving students a map is certainly less time consuming than running a fire drill, so why don’t we just give students a map?
Math educators are on a never ending quest to help students improve their problem solving skills. To succeed on this quest, they must choose between a variety of tools and it can be challenging to determine which are better. So, I wanted to share my take on two main categories I see:
problem solving tools designed for complicated situations
problem solving tools designed for complex situations
Consider the two problems on adding two-digit numbers shown below that are of varying Depth of Knowledge (DOK) levels.
When I gave both of these problems to my then second-grade son (who is fortunately a mini-math geek like his dad), he quickly conquered Problem One with it providing no real challenge. When I showed him Problem Two, he got 98 + 76. This is a great first answer, but it’s wrong.
He knew which four numbers to use but the problem exposed a hole in his understanding of place value and gave me a great opportunity to ask him questions like, “What does the 9 represent? What does the 8 represent? How does having more tens or ones change the sum?”
I’d make the case that the problem on the left is DOK 1 while the problem on the right is DOK 3 (more info here). Recently though, I got some pushback that forced me to think of a new way to articulate the difference between them.
From 2010 to 2013, I had the opportunity to facilitate approximately 70 lesson study days with third grade through high school math teachers in my district. It was one of the best experiences of my career as my job was focused on learning about how students learn. So, I thought it would be worthwhile to share some of the lessons learned (many the hard way) as I believe that other educators may find them useful.
First, let me describe the lesson study process we used:
If you’ve put up your #ObserveMe sign but things aren’t going the way you hoped, then this post’s for you. I’m using this as a running list of solutions for problems that educators are encountering so we can have them in a central location. Here’s how you can help:
Are you encountering issues that aren’t listed?
Do you have solutions that aren’t listed?
If so, please mention them in the comments and I will add them.
I wanted to share my responses to the four questions I am most frequently asked about Depth of Knowledge (DOK). Those questions are: “When will students ever use this?”, “What DOK level should I start students off with?”, “How do teachers fit these problems into their pacing?”, and “How do I help prevent students from giving up after trying the problem once or twice?”
Here are two ways to integrate a problem-based lesson into your unit as well as a third that should be avoided. I use an 8th grade standard on the volume of spheres, cones, and cylinders as an example.
I realized this weekend that if I am suggesting that we should all ask people to observe one another (#ObserveMe), then I should follow my own advice in as public a way as possible. So, I would like any interested peers to give me feedback on the goals in the picture below and record it on this Google Form. I believe that it may also be useful to read the feedback others are leaving for me. So, you can see everyone’s feedback here.
A teacher who doesn’t collaborate works on an isolated island. When this lack of collaboration permeates an entire school, teachers more closely resemble independent contractors than colleagues. I’m growing increasingly concerned that this is becoming more, and not less, common. Consider the highly shared and liked tweet below from Heather Kohn. At a very collaborative…